山东省淄博市张店区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
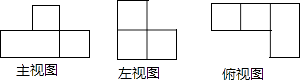
1. 下列解析式中,y不是x的函数的是( ).A、 B、 C、 D、2. 图中的三视图所对应的几何体是( )
 A、
A、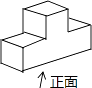 B、
B、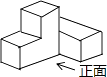 C、
C、 D、
D、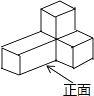 3. 已知反比例函数 ,则该反比例函数的图象经过哪几个象限A、一、二象限 B、一、三象限 C、二、三象限 D、二、四象限4. 平面内有两点P、O,⊙O的半径为1,若 ,则点P与⊙O的位置关系是( ).A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、无法判断5. 在二次函数 的图像中,若 随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、6. 如图,为方便行人推车过天桥,某市政府在 高的天桥两端分别修建了 长的斜道,用科学计算器计算这条斜道的倾斜角 ,下列按键顺序正确的是( ).
3. 已知反比例函数 ,则该反比例函数的图象经过哪几个象限A、一、二象限 B、一、三象限 C、二、三象限 D、二、四象限4. 平面内有两点P、O,⊙O的半径为1,若 ,则点P与⊙O的位置关系是( ).A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、无法判断5. 在二次函数 的图像中,若 随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、6. 如图,为方便行人推车过天桥,某市政府在 高的天桥两端分别修建了 长的斜道,用科学计算器计算这条斜道的倾斜角 ,下列按键顺序正确的是( ). A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,有一个半径为 的圆形纸片,若在该纸片上沿虚线剪一个最大正六边形纸片,则这个正六边形纸片的边心距是( ).
7. 如图,有一个半径为 的圆形纸片,若在该纸片上沿虚线剪一个最大正六边形纸片,则这个正六边形纸片的边心距是( ).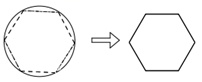 A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 是一个光源.木杆AB两端的坐标分别为 , .则木杆AB在x轴上的投影长为( ).
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 是一个光源.木杆AB两端的坐标分别为 , .则木杆AB在x轴上的投影长为( ).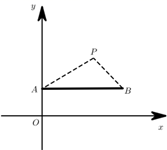 A、4 B、5 C、6 D、89. 如图,在 中, , , ,⊙O是 的内切圆,则⊙O的半径为( )
A、4 B、5 C、6 D、89. 如图,在 中, , , ,⊙O是 的内切圆,则⊙O的半径为( )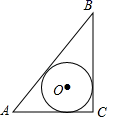 A、1 B、 C、2 D、10. 表给出了二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的部分对应值:那么方程ax2+bx+c=0的一个根的近似值可能是( )
A、1 B、 C、2 D、10. 表给出了二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y的部分对应值:那么方程ax2+bx+c=0的一个根的近似值可能是( )x
…
1
1.1
1.2
1.3
1.4
…
y
…
﹣1
﹣0.49
0.04
0.59
1.16
…
A、1.08 B、1.18 C、1.28 D、1.3811. 如图,在 中,O是BC边上的点,以点O为圆心,BO为半径的⊙O与AC相切于点A,D是优弧AB上一点, ,则 的度数是( ).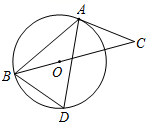 A、65° B、50° C、40° D、30°12. 如图是抛物线 图象的一部分,抛物线的顶点坐标是 ,与x轴的一个交点 ,直线 与抛物线交于A、B两点.下列结论:
A、65° B、50° C、40° D、30°12. 如图是抛物线 图象的一部分,抛物线的顶点坐标是 ,与x轴的一个交点 ,直线 与抛物线交于A、B两点.下列结论:① ;② ;③方程 有两个不相等的实数根;④抛物线与x轴的另一个交点是 ;⑤ (q实数).其中正确的是( ).
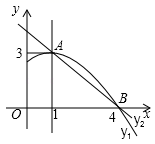 A、①②③ B、①③④ C、②④⑤ D、③④⑤
A、①②③ B、①③④ C、②④⑤ D、③④⑤二、填空题
-
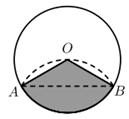
13. 已知抛物线的解析式为 ,则抛物线的顶点坐标为 .14. 双曲线 与直线 相交于A、B两点,B点坐标为 ,则A点坐标为 .15. 如图,将半径为3的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形AOB围成一个圆锥的侧面,则这个圆锥底面圆的半径为 .
 16. 如图,单孔拱桥的形状近似抛物线形,建立如图所示的平面直角坐标系,在正常水位时,水面宽度OA为 ,拱桥的最高点B到水面OA的距离为 .则抛物线的解析式为 .
16. 如图,单孔拱桥的形状近似抛物线形,建立如图所示的平面直角坐标系,在正常水位时,水面宽度OA为 ,拱桥的最高点B到水面OA的距离为 .则抛物线的解析式为 .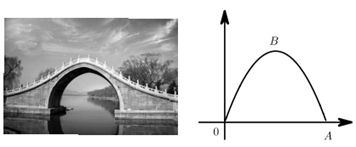 17. 如图,一次函数 与反比例函数 的图象在第一象限交于点A,点C在以 为圆心,1为半径的⊙B上,已知当点C到直线OA的距离最大时 的面积为8,则该反比例函数的表达式为 .
17. 如图,一次函数 与反比例函数 的图象在第一象限交于点A,点C在以 为圆心,1为半径的⊙B上,已知当点C到直线OA的距离最大时 的面积为8,则该反比例函数的表达式为 .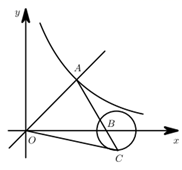
三、解答题
-
18. 计算:(1)、 .(2)、19. 如图,在⊙O中,AB为直径,BP为⊙O的弦,AC与BP的延长线交于点C,且 , 于点E,求证:PE是⊙O的切线.
 20. 如图,一次函数 与反比例函数 的图象交于 、 两点.
20. 如图,一次函数 与反比例函数 的图象交于 、 两点.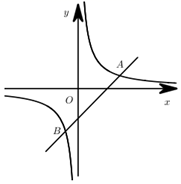 (1)、求反比例函数和一次函数的表达式.(2)、请直接写出不等式 的解集,(3)、点P是x轴上的一点,若 的面积是6,求点P的坐标.21. 如图,李明在大楼27米高(即 米)的窗口P处进行观测,测得山坡上A处的俯角 ,山脚B处的俯角 ,已知该山坡的坡度i(即 )为 .点P、H、B、C、A在同一个平面内.点H、B、C、在同一条直线上,且 .
(1)、求反比例函数和一次函数的表达式.(2)、请直接写出不等式 的解集,(3)、点P是x轴上的一点,若 的面积是6,求点P的坐标.21. 如图,李明在大楼27米高(即 米)的窗口P处进行观测,测得山坡上A处的俯角 ,山脚B处的俯角 ,已知该山坡的坡度i(即 )为 .点P、H、B、C、A在同一个平面内.点H、B、C、在同一条直线上,且 .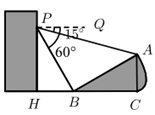 (1)、山坡坡角(即 )的度数等于度.(2)、求AB的长(结果保留根号).22. 某市体育馆为了让体育运动的人方便停车,体育馆利用一块矩形空地建了一个停车场,其布局如图所示,已知停车场的长为58米,宽为22米,阴影部分为停车位,其余部分是等宽的通道,已知停车位的面积为700平方米.
(1)、山坡坡角(即 )的度数等于度.(2)、求AB的长(结果保留根号).22. 某市体育馆为了让体育运动的人方便停车,体育馆利用一块矩形空地建了一个停车场,其布局如图所示,已知停车场的长为58米,宽为22米,阴影部分为停车位,其余部分是等宽的通道,已知停车位的面积为700平方米.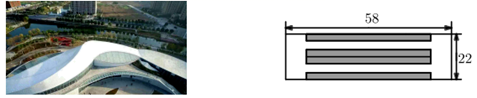 (1)、求通道的宽是多少米?(2)、该停车场共有车位70个,据调查分析,当每个车位的月租金为300元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位,那么停车场的月租金收入最大为多少元?23. ⊙O是四边形APBC的外接圆,连接AB、CP,且 .(1)、如图1,若 ,判断 的形状,并说明理由.
(1)、求通道的宽是多少米?(2)、该停车场共有车位70个,据调查分析,当每个车位的月租金为300元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位,那么停车场的月租金收入最大为多少元?23. ⊙O是四边形APBC的外接圆,连接AB、CP,且 .(1)、如图1,若 ,判断 的形状,并说明理由.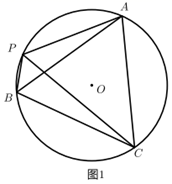 (2)、在(1)的条件下,若 , ,求PC的长.(3)、如图2,若 ,请判断BP、AP、CP之间的数量关系(用含 的代数式表示),并说明理由.
(2)、在(1)的条件下,若 , ,求PC的长.(3)、如图2,若 ,请判断BP、AP、CP之间的数量关系(用含 的代数式表示),并说明理由.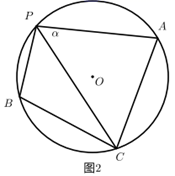 24.(1)、探究新知:如图1,已知 与 的面积相等,试判断AB与CD的位置关系,并说明理由.
24.(1)、探究新知:如图1,已知 与 的面积相等,试判断AB与CD的位置关系,并说明理由.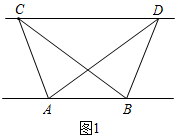 (2)、结论应用:如图2,点M,N在反比例函数 的图象上,过点M作 轴,过点N 作 轴,垂足分别为E,F.试证明: .
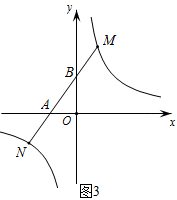
(2)、结论应用:如图2,点M,N在反比例函数 的图象上,过点M作 轴,过点N 作 轴,垂足分别为E,F.试证明: .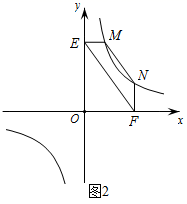 (3)、拓展延伸:若(2)中的其他条件不变,只改变点M,N在反比例函数 图象上的位置,如图3所示,MN与x轴、y轴分别交于点A、点B,若 ,请求AN的长.
(3)、拓展延伸:若(2)中的其他条件不变,只改变点M,N在反比例函数 图象上的位置,如图3所示,MN与x轴、y轴分别交于点A、点B,若 ,请求AN的长.