山东省淄博市临淄区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 关于二次函数 ,下列说法正确的是( )A、图象的对称轴在 轴的右侧 B、图象与 轴的交点坐标为 C、图象与 轴的交点坐标为 和 D、 的最小值为-92. 如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )
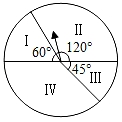 A、 B、 C、 D、3. 已知某几何体的三视图如图所示,则该几何体可能是( )
A、 B、 C、 D、3. 已知某几何体的三视图如图所示,则该几何体可能是( )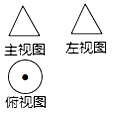 A、
A、 B、
B、 C、
C、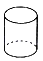 D、
D、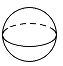 4. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
4. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、 B、
B、 C、
C、 D、
D、 5. 在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )A、 B、 C、 D、6. Rt△ABC中,∠C=90°,AB=5,cosA= ,以点B为圆心,r为半径作⊙B,当r=3时,⊙B与AC的位置关系是( )A、相离 B、相切 C、相交 D、无法确定7. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为( ).
5. 在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )A、 B、 C、 D、6. Rt△ABC中,∠C=90°,AB=5,cosA= ,以点B为圆心,r为半径作⊙B,当r=3时,⊙B与AC的位置关系是( )A、相离 B、相切 C、相交 D、无法确定7. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为( ). A、 B、 C、 D、8. 如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y= (k≠0)的图象上,则反比例函数的解析式为( )
A、 B、 C、 D、8. 如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y= (k≠0)的图象上,则反比例函数的解析式为( ) A、y= B、y= C、y= D、y=9. 如图,二次函数 的图象与 轴交于 ,B两点,下列说法错误的是( )
A、y= B、y= C、y= D、y=9. 如图,二次函数 的图象与 轴交于 ,B两点,下列说法错误的是( )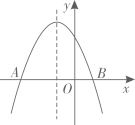 A、 B、图象的对称轴为直线 C、点B的坐标为 D、当 时,y随x的增大而增大10. 若函数 的图象如图所示,则函数 和 在同一平面直角坐标系中的图象大致是( )
A、 B、图象的对称轴为直线 C、点B的坐标为 D、当 时,y随x的增大而增大10. 若函数 的图象如图所示,则函数 和 在同一平面直角坐标系中的图象大致是( )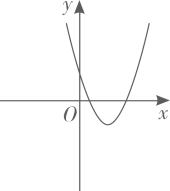 A、
A、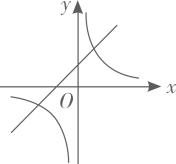 B、
B、 C、
C、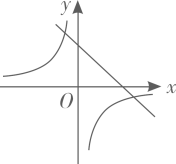 D、
D、 11. 如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是( )
11. 如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是( )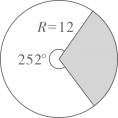 A、3.6 B、1.8 C、3 D、612. 如图,在平面直角坐标系中,直线 与双曲线 交于 、 两点, 是以点 为圆心,半径长 的圆上一动点,连结 , 为 的中点.若线段 长度的最大值为2,则 的值为( )
A、3.6 B、1.8 C、3 D、612. 如图,在平面直角坐标系中,直线 与双曲线 交于 、 两点, 是以点 为圆心,半径长 的圆上一动点,连结 , 为 的中点.若线段 长度的最大值为2,则 的值为( ) A、 B、 C、-2 D、
A、 B、 C、-2 D、二、填空题
-
13. 若二次函数 的图象与x轴有两个交点,则k的取值范围是.14. 如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离 为海里.
 15. 从-1,2,-3,4这四个数中任取两个不同的数分别作为a,b的值,得到反比例函数 ,则这些反比例函数中,其图象在二、四象限的概率是 .16. 如图,直径AB为6的半圆,绕 点顺时针旋转 ,此时点 到了点 ,则图中阴影部分的面积是 .
15. 从-1,2,-3,4这四个数中任取两个不同的数分别作为a,b的值,得到反比例函数 ,则这些反比例函数中,其图象在二、四象限的概率是 .16. 如图,直径AB为6的半圆,绕 点顺时针旋转 ,此时点 到了点 ,则图中阴影部分的面积是 . 17. 如图,在直角坐标系中,以坐标原点O(0,0),A(0,4),B(3,0)为顶点的Rt△AOB,其两个锐角对应的外角角平分线相交于点P,且点P恰好在反比例函数y= 的图象上,则k的值为 .
17. 如图,在直角坐标系中,以坐标原点O(0,0),A(0,4),B(3,0)为顶点的Rt△AOB,其两个锐角对应的外角角平分线相交于点P,且点P恰好在反比例函数y= 的图象上,则k的值为 .
三、解答题
-
18.(1)、如图是一个几何体的三视图,依据图中给出的数据,求出这个几何体的侧面积.
 (2)、如图2是图1长方体的三视图,若用S表示面积,S主=a2 , S左=a2+a,求出S俯 .
(2)、如图2是图1长方体的三视图,若用S表示面积,S主=a2 , S左=a2+a,求出S俯 . 19. 如图,已知反比例函数 的图象与直线 相交于点 , .
19. 如图,已知反比例函数 的图象与直线 相交于点 , . (1)、求出直线 的表达式;(2)、在x轴上有一点 使得 的面积为18,求出点P的坐标.20. 刘雨泽和黎昕两位同学玩抽数字游戏.五张卡片上分别写有2、4、6、8、 这五个数字,其中两张卡片上的数字是相同的,从中随机抽出一张,已知 (抽到数字4的卡片) .(1)、求这五张卡片上的数字的众数;(2)、若刘雨泽已抽走一张数字2的卡片,黎昕准备从剩余4张卡片中抽出一张.
(1)、求出直线 的表达式;(2)、在x轴上有一点 使得 的面积为18,求出点P的坐标.20. 刘雨泽和黎昕两位同学玩抽数字游戏.五张卡片上分别写有2、4、6、8、 这五个数字,其中两张卡片上的数字是相同的,从中随机抽出一张,已知 (抽到数字4的卡片) .(1)、求这五张卡片上的数字的众数;(2)、若刘雨泽已抽走一张数字2的卡片,黎昕准备从剩余4张卡片中抽出一张.①所剩的4张卡片上数字的中位数与原来5张卡片上数字的中位数是否相同?并简要说明理由;
②黎昕先随机抽出一张卡片后放回,之后又随机抽出一张,用列表法(或树状图)求黎昕两次都抽到数字4的概率.
21. 图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图,经测量,钢条AB=AC=50cm,∠ABC=47°.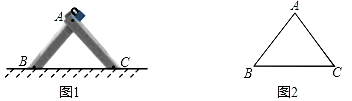 (1)、求车位锁的底盒长BC.(2)、若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位?(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)22. 已知:如图,AB、AC是⊙O的两条弦,且AB=AC,D是AO延长线上一点,联结BD并延长交⊙O于点E,联结CD并延长交⊙O于点F.
(1)、求车位锁的底盒长BC.(2)、若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位?(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)22. 已知:如图,AB、AC是⊙O的两条弦,且AB=AC,D是AO延长线上一点,联结BD并延长交⊙O于点E,联结CD并延长交⊙O于点F.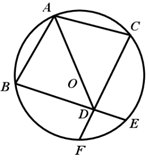 (1)、求证:BD=CD:(2)、如果AB2=AO·AD,求证:四边形ABDC是菱形.23. 某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
(1)、求证:BD=CD:(2)、如果AB2=AO·AD,求证:四边形ABDC是菱形.23. 某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:销售单价x(元/千克)
55
60
65
70
销售量y(千克)
70
60
50
40
(1)、求y(千克)与x(元/千克)之间的函数表达式;(2)、为保证某天获得600元的销售利润,则该天的销售单价应定为多少?(3)、当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?24. 如图,⊙O为等边△ABC的外接圆,半径为2,点D在劣弧 上运动(不与点A,B重合),连接DA,DB,DC.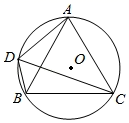 (1)、求证:DC是∠ADB的平分线;(2)、四边形ADBC的面积S是线段DC的长x的函数吗?如果是,求出函数解析式;如果不是,请说明理由;(3)、若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置,△DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.
(1)、求证:DC是∠ADB的平分线;(2)、四边形ADBC的面积S是线段DC的长x的函数吗?如果是,求出函数解析式;如果不是,请说明理由;(3)、若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置,△DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.