山东省枣庄市薛城区2020-2021学年九年级上学期期末考试数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 方程 ${(x + 1)}^{2} = 4$ 的解为（）

A、 $x_{1} = 1 ， x_{2} = - 1$ B、 $x_{1} = - 1 ， x_{2} = 3$ C、 $x_{1} = 2 ， x_{2} = - 2$ D、 $x_{1} = 1 ， x_{2} = - 3$

查看试题解析
2. 已知α为锐角，且sin（α﹣10°）＝ $\frac{\sqrt{3}}{2}$ ，则α等于（　　）

A、70° B、60° C、50° D、30°

查看试题解析
3. 已知反比例函数y＝2x^﹣¹ ，下列结论中，错误的是（）

A、点（﹣2，﹣1）在它的图象上 B、y随x的增大而减小 C、图象在第一、三象限 D、若x＜0时，y随x的增大而减小

查看试题解析
4. 一个不透明的袋子里装有两双只有颜色不同的手套，小明已经摸出一只手套，他再任意摸取一只，恰好两只手套凑成同一双的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、1

查看试题解析
5. 某药品原价为100元，连续两次降价 $a %$ 后，售价为64元，则 $a$ 的值为（）

A、10 B、20 C、23 D、36

查看试题解析
6. 将函数 $y = x^{2}$ 的图象向右平移1个单位，再向下平移3个单位，可得到的抛物线是（）

A、 $y = {(x - 1)}^{2} - 3$ B、 $y = {(x - 1)}^{2} + 3$ C、 $y = {(x + 1)}^{2} + 3$ D、 $y = {(x + 1)}^{2} - 3$

查看试题解析
7. 如图，在平面直角坐标系xOy中，正方形ABCD的顶点D在y轴上且A(﹣3，0)，B(2，b)，则正方形ABCD的面积是（）

A、20 B、16 C、34 D、25

查看试题解析
8. 已知反比例函数 $y = - \frac{7}{x}$ 图像上三个点的坐标分别是 $A (- 2 ， y_{1}) 、 B (1 ， y_{2}) 、 C (2 ， y_{3})$ ，能正确反映 $y_{1} ， y_{2} ， y_{3}$ 的大小关系的是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{2} > y_{1} > y_{3}$ D、 $y_{2} > y_{3} > y_{1}$

查看试题解析
9. 定义：在等腰三角形中，底边与腰的比叫做顶角的正对，顶角 $A$ 的正对记作 $s a d A$ ，即 $s a d A =$ 底边：腰.如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ A = 2 ∠ B$ .则 $\sin B \cdot s a d A =$ （）

A、 $\frac{1}{2}$ B、 $\sqrt{2}$ C、1 D、2

查看试题解析
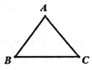10. 用小立方块搭成的几何体，从正面看和从上面看的形状图如下，则组成这样的几何体需要的立方块个数为（）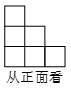

A、最多需要8块，最少需要6块 B、最多需要9块，最少需要6块 C、最多需要8块，最少需要7块 D、最多需要9块，最少需要7块

查看试题解析
11. 如图，在△ABC中，AD⊥BC交BC于点D，AD＝BD，若AB＝ $4 \sqrt{2}$ ，tanC＝ $\frac{4}{3}$ ，则BC＝（）

A、8 B、 $8 \sqrt{2}$ C、7 D、 $7 \sqrt{2}$

查看试题解析
12. 已知二次函数y＝ax²+bx+c的图象如图所示，下列结i论：①abc＞0；②b²﹣4ac＞0；③2a+b＝0；④a﹣b+c＜0．其中正确的结论有（）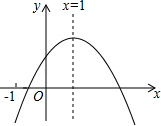

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 若关于x的一元二次方程（a﹣1）x²﹣2x+2=0有实数根，则整数a的最大值为．

查看试题解析
14. 已知点P是正方形ABCD内部一点，且 $△ P A B$ 是正三角形，则∠CPD=度．

查看试题解析
15. 已知m,n是方程 $x^{2} - x - 2 = 0$ 的两个根，则代数式 $2 m^{2} - 3 m - n$ 的值是．

查看试题解析
16. 如图，从甲楼底部A处测得乙楼顶部C处的仰角是30°，从甲楼顶部B处测得乙楼底部D处的俯角是45°，已知甲楼的高AB是120m，则乙楼的高CD是m（结果保留根号）

查看试题解析
17. 如图，点B是反比例函数y＝ $\frac{k}{x}$ 图象上的一点，矩形OABC的周长是20，正方形OCDF与正方形BCGH的面积之和为68，则k的值为

查看试题解析
18. 如图，一名男生推铅球，铅球行进高度 $y$ （单位：m）与水平距离 $x$ （单位：m）之间的关系是 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ．则他将铅球推出的距离是m．

查看试题解析
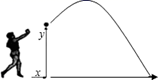19. 已知p，q都是正整数，方程7x²﹣px+2009q＝0的两个根都是质数，则p+q＝．

查看试题解析
20. 如图，正方形ABCD的边长为6，点E，F分别在AB，AD上，若CE= $3 \sqrt{5}$ ，且∠ECF=45°，则CF的长为．

查看试题解析

三、解答题

21. 计算： $| - \sqrt{3} | + \sqrt{3} \cos 30^{\circ} - {(- \frac{1}{3})}^{- 1} - \sqrt{12} + {(π - 3)}^{0}$

查看试题解析
22.
小红想利用阳光下的影长测量学校旗杆AB的高度．如图，他在某一时刻在地面上竖直立一个2米长的标杆CD，测得其影长DE=0.4米．

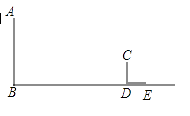(1)、请在图中画出此时旗杆AB在阳光下的投影BF．

(2)、如果BF=1.6，求旗杆AB的高．

查看试题解析
23. 速滑运动受到许多年轻人的喜爱。如图，四边形 $B C D G$ 是某速滑场馆建造的滑台，已知 $C D / / E G$ ，滑台的高 $D G$ 为 $5$ 米，且坡面 $B C$ 的坡度为 $1 ： 1$ .后来为了提高安全性，决定降低坡度，改造后的新坡面AC的坡度为 $1 ： \sqrt{3}$ .

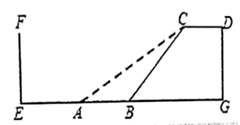(1)、求新坡面 $A C$ 的坡角及 $A C$ 的长；

(2)、原坡面底部 $B G$ 的正前方 $10$ 米处 $(E B = 10)$ 是护墙 $E F$ ，为保证安全，体育管理部门规定，坡面底部至少距护墙 $7$ 米。请问新的设计方案能否通过，试说明理由（参考数据： $\sqrt{3} \approx 1.73$ ）

查看试题解析
24. 某商场购进一种单价为10元的商品，根据市场调查发现：如果以单价20元售出，那么每天可卖出30个，每降价1元，每天可多卖出5个，若每个降价x（元），每天销售y（个），每天获得利润W（元）．

(1)、写出y与x的函数关系式；

(2)、求W与x的函数关系式（不必写出x的取值范围）

(3)、若降价x元（x不低于4元）时，销售这种商品每天获得的利润最大为多少元？

查看试题解析
25. 如图，在平面直角坐标系中，一次函数y＝ax+b的图象与反比例函数y＝ $\frac{k}{x}$ 的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，﹣4），连接AO，AO＝5，sin∠AOC＝ $\frac{3}{5}$ ．

(1)、求反比例函数和一次函数的解析式；

(2)、连接OB，求△AOB的面积．

查看试题解析
26. 如图，在四边形ABCD中，AB⊥AD， $\frac{AD}{AB}$ ＝ $\frac{3}{4}$ ，对角线AC与BD交于点O，AC＝10，∠ABD＝∠ACB，点E在CB延长线上，且AE＝AC．

(1)、求证：△AEB∽△BCO；

(2)、当AE∥BD时，求AO的长．

查看试题解析
27. 如图，抛物线y＝ax²+2x+c经过点A（0，3），B（﹣1，0），请解答下列问题：

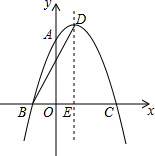(1)、求抛物线的解析式；

(2)、抛物线的顶点为点D，对称轴与x轴交于点E，连接BD，求BD的长；

(3)、点F在抛物线上运动，是否存在点F，使△BFC的面积为6，如果存在，求出点F的坐标；如果不存在，请说明理由.

查看试题解析
28. 已知在平面直角坐标中，点A(m，n)在第一象限内，AB⊥OA且AB=OA，反比例函数y= $\frac{k}{x}$ 的图象经过点A

(1)、当点B的坐标为(4，0)时（如图1），求这个反比例函数的解析式；

(2)、当点B在反比例函数y= $\frac{k}{x}$ 的图象上，且在点A的右侧时（如图2），用含字母m，n的代数式表示点B的坐标；

(3)、在第（2）小题的条件下，求 $\frac{m}{n}$ 的值．

查看试题解析