山东省枣庄市台儿庄区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 如图,将小立方块①从6个大小相同的小立方块所搭的几何体中移走后,所得几何体( )
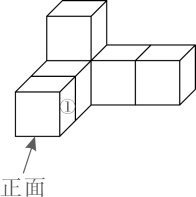 A、主视图改变,左视图改变 B、俯视图不变,左视图改变 C、俯视图改变,左视图改变 D、主视图不变,左视图不变2. 一元二次方程 的解是( )A、 , B、 , C、 , D、 ,3. 反比例函数 经过点 ,则下列说法错误的是( )A、 B、函数图象分布在第一、三象限 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小4. 如图所示, 的顶点在正方形网格的格点上,则 的值为( )
A、主视图改变,左视图改变 B、俯视图不变,左视图改变 C、俯视图改变,左视图改变 D、主视图不变,左视图不变2. 一元二次方程 的解是( )A、 , B、 , C、 , D、 ,3. 反比例函数 经过点 ,则下列说法错误的是( )A、 B、函数图象分布在第一、三象限 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小4. 如图所示, 的顶点在正方形网格的格点上,则 的值为( )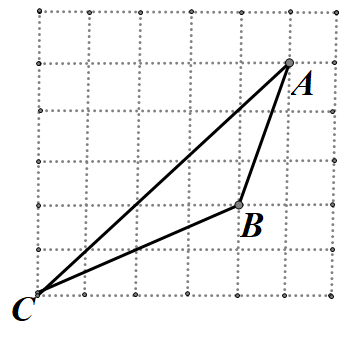 A、 B、 C、2 D、5. 反比例函数 的图象上有两点 , ,若 ,则下列结论正确的是( )A、 B、 C、 D、6. 将抛物线 向上平移3个单位长度,再向右平移5个单位长度,所得的抛物线为( )A、 B、 C、 D、7. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
A、 B、 C、2 D、5. 反比例函数 的图象上有两点 , ,若 ,则下列结论正确的是( )A、 B、 C、 D、6. 将抛物线 向上平移3个单位长度,再向右平移5个单位长度,所得的抛物线为( )A、 B、 C、 D、7. 如图, 中, ,点D在 上, .若 ,则 的长度为( )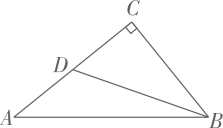 A、 B、 C、 D、48. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
A、 B、 C、 D、48. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、 B、
B、 C、
C、 D、
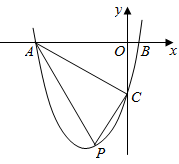
D、 9. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、10. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
9. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、10. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )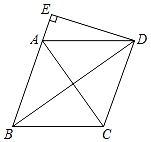 A、 B、 C、4 D、11. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ac>0;②abc<0;③4a+b=0;④4a﹣2b+c>0.其中正确结论的个数是( )
A、 B、 C、4 D、11. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ac>0;②abc<0;③4a+b=0;④4a﹣2b+c>0.其中正确结论的个数是( ) A、4 B、3 C、2 D、112. 如图, , ,点A在 上,四边形 是矩形,连接 、 交于点E,连接 交 于点F.下列4个判断:① 平分 ;② ;③ ;④若点G是线段 的中点,则 为等腰直角三角形.正确判断的个数是( )
A、4 B、3 C、2 D、112. 如图, , ,点A在 上,四边形 是矩形,连接 、 交于点E,连接 交 于点F.下列4个判断:① 平分 ;② ;③ ;④若点G是线段 的中点,则 为等腰直角三角形.正确判断的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 计算: =14. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是 .
 15. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .16. 如图,在 中,D,E为边 的三等分点, ,H为 与 的交点.若 ,则 .
15. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .16. 如图,在 中,D,E为边 的三等分点, ,H为 与 的交点.若 ,则 .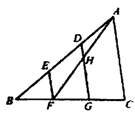 17. 如图,在平面直角坐标系中,矩形ABCD的边AB在y轴上,点C坐标为(2,﹣2),并且AO:BO=1:2,点D在函数y= (x>0)的图象上,则k的值为 .
17. 如图,在平面直角坐标系中,矩形ABCD的边AB在y轴上,点C坐标为(2,﹣2),并且AO:BO=1:2,点D在函数y= (x>0)的图象上,则k的值为 .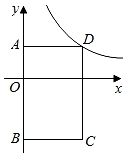 18. 如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .
18. 如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .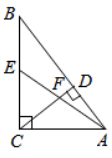
三、解答题
-
19. 计算:20. 如图,一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
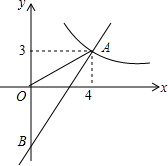 (1)、求函数y=kx+b和y= 的表达式;(2)、已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.21. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.
(1)、求函数y=kx+b和y= 的表达式;(2)、已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.21. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.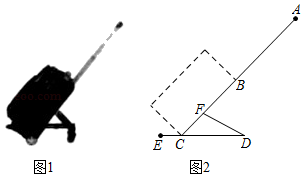 (1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).22. 如图,在矩形 中,对角线 的垂直平分线分别与边 和边 的延长线交于点 , ,与边 交于点 ,垂足为点 .
(1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).22. 如图,在矩形 中,对角线 的垂直平分线分别与边 和边 的延长线交于点 , ,与边 交于点 ,垂足为点 .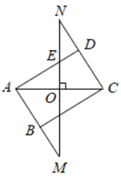 (1)、求证: ;(2)、若 , ,请直接写出 的长为 .
(1)、求证: ;(2)、若 , ,请直接写出 的长为 .