山东省烟台招远市(五四制)2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 已知 为锐角,且 ,则 ( )A、 B、 C、 D、2. 平面内,⊙O的半径为1,点P到O的距离为3,过点P可作⊙O的切线条数为( )A、0条 B、1条 C、2条 D、无数条3. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
 A、 B、 C、 D、4. 一人乘雪橇沿坡比1: 的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为s=8t+2t2 , 若滑到坡底的时间为5s,则此人下降的高度为( )
A、 B、 C、 D、4. 一人乘雪橇沿坡比1: 的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为s=8t+2t2 , 若滑到坡底的时间为5s,则此人下降的高度为( )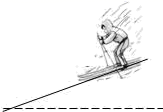 A、90 m B、45m C、45 m D、90m5. 如图,AB是⊙O直径,若∠AOC=150°,则∠D的度数是( )
A、90 m B、45m C、45 m D、90m5. 如图,AB是⊙O直径,若∠AOC=150°,则∠D的度数是( )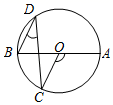 A、15° B、25° C、30° D、75°6. 二次函数y=﹣2(x+2)2﹣4,下列说法正确的是( )A、开口向上 B、对称轴为直线x=2 C、顶点坐标为(-2,4) D、当x<﹣2时,y随x的增大而增大7. 如图,A,B,C,三点在正方形网格线的交点处,若将 绕着点A逆时针旋转得到 ,则 的值为( )
A、15° B、25° C、30° D、75°6. 二次函数y=﹣2(x+2)2﹣4,下列说法正确的是( )A、开口向上 B、对称轴为直线x=2 C、顶点坐标为(-2,4) D、当x<﹣2时,y随x的增大而增大7. 如图,A,B,C,三点在正方形网格线的交点处,若将 绕着点A逆时针旋转得到 ,则 的值为( )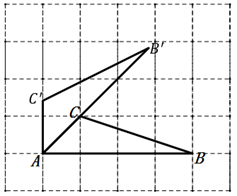 A、 B、 C、 D、8. 如图,AB为⊙O直径,CD为弦,AB⊥CD于E,连接CO,AD,∠BAD=25°,下列结论中正确的有( )
A、 B、 C、 D、8. 如图,AB为⊙O直径,CD为弦,AB⊥CD于E,连接CO,AD,∠BAD=25°,下列结论中正确的有( )①CE=OE;②∠C=40°;③ = ;④AD=2OE
 A、①④ B、②③ C、②③④ D、①②③④9. 如图,A、B是曲线y= 上的点,经过A、B两点向x轴、y轴作垂线段,若S阴影=1.5,则S1+S2=( )
A、①④ B、②③ C、②③④ D、①②③④9. 如图,A、B是曲线y= 上的点,经过A、B两点向x轴、y轴作垂线段,若S阴影=1.5,则S1+S2=( )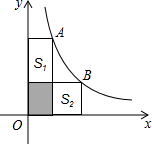 A、4 B、5 C、6 D、710. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A、4 B、5 C、6 D、710. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )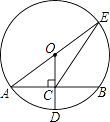 A、2 B、8 C、2 D、211. 如图,抛物线y=﹣x2+2x+2交y轴于点A , 与x轴的一个交点在2和3之间,顶点为B . 下列说法:其中正确判断的序号是( )
A、2 B、8 C、2 D、211. 如图,抛物线y=﹣x2+2x+2交y轴于点A , 与x轴的一个交点在2和3之间,顶点为B . 下列说法:其中正确判断的序号是( )①抛物线与直线y=3有且只有一个交点;②若点M(﹣2,y1),N(1,y2),P(2,y3)在该函数图象上,则y1<y2<y3;③将该抛物线先向左,再向下均平移2个单位,所得抛物线解析式为y=(x+1)2+1;④在x轴上找一点D , 使AD+BD的和最小,则最小值为 .
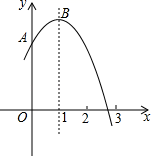 A、①②④ B、①②③ C、①③④ D、②③④12. 如图,抛物线 与 轴交于 、 两点, 是以点 (0,3)为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是( )
A、①②④ B、①②③ C、①③④ D、②③④12. 如图,抛物线 与 轴交于 、 两点, 是以点 (0,3)为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
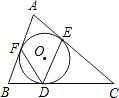
13. 函数 中,自变量 的取值范围是 .14. 正六边形的半径与边心距之比为 .15. 若二次函数y=x2﹣(m﹣1)x的图象经过点(3,0),则关于x的一元二次方程x2﹣(m﹣1)x=0的根为 .16. 半径为5的圆内有长为5 的弦,则此弦所对的圆周角为17. 如图,⊙O是△ABC的内切圆,与边BC,CA,AB的切点分别为D,E,F,若∠A=70°,则∠EDF=度.
 18. 如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为 .
18. 如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为 .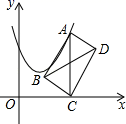
三、解答题
-
19. 计算:(1)、2sin30°+3cos60°+tan45°;(2)、 ﹣|﹣3|+( )-2﹣4cos30°.20. 文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以不选以上四类而写出一个自己最喜爱的其他文化栏目(这时记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
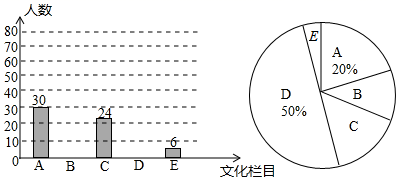
请根据图中信息解答下列问题:
(1)、在这项调查中,共调查了名学生;(2)、最喜爱《朗读者》的学生有名;(3)、扇形统计图中“B”所在扇形圆心角的度数为;(4)、选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请直接写出:刚好选到一名男生和一名女生的概率为 .21. 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.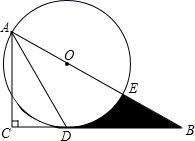 (1)、判断直线BC与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为6,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.22. 某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.(1)、求w与x之间的函数关系式;(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少.23. 如图分别是某款篮球架的实物图与示意图,已知 于点 ,底座 的长为1米,底座 与支架 所成的角 ,点 在支架 上,篮板底部支架 于点 ,已知 长 米, 长 米, 长1米.
(1)、判断直线BC与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为6,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.22. 某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.(1)、求w与x之间的函数关系式;(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少.23. 如图分别是某款篮球架的实物图与示意图,已知 于点 ,底座 的长为1米,底座 与支架 所成的角 ,点 在支架 上,篮板底部支架 于点 ,已知 长 米, 长 米, 长1米. (1)、求篮板底部支架 与 支架所成的角 的度数.(2)、求篮板底部点 到地面的距离.(结果保留根号)
(1)、求篮板底部支架 与 支架所成的角 的度数.(2)、求篮板底部点 到地面的距离.(结果保留根号)