山东省烟台市龙口市2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
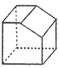
1. 已知∠α为锐角,且tanα=1,则sinα的值为( )A、45° B、 C、 D、2. 如图所示的几何体,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列函数中,当x>0时,y随x的增大而减小的是( )A、y=x2 B、y=x﹣1 C、y= D、y=﹣x24. 用计算器求 的值,以下按键顺序正确的是( )A、
3. 下列函数中,当x>0时,y随x的增大而减小的是( )A、y=x2 B、y=x﹣1 C、y= D、y=﹣x24. 用计算器求 的值,以下按键顺序正确的是( )A、 B、
B、 C、
C、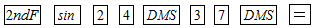 D、
D、 5. 已知点P(a,b)在反比例函数 的图象上,点M(﹣b,a)在反比例函数 的图象上,则k的值为( )A、﹣5 B、5 C、 D、无法确定6. 如图,点O是正五边形ABCDE的中心,⊙O是正五边形的外接圆,∠ADE的度数为( )
5. 已知点P(a,b)在反比例函数 的图象上,点M(﹣b,a)在反比例函数 的图象上,则k的值为( )A、﹣5 B、5 C、 D、无法确定6. 如图,点O是正五边形ABCDE的中心,⊙O是正五边形的外接圆,∠ADE的度数为( )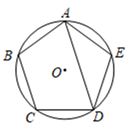 A、30° B、32° C、36° D、40°7. 将抛物线y=(x+2)2先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的表达式为( )A、y=(x+3)2-2 B、y=(x+3)2+2 C、y=(x+1)2+2 D、y=(x+1)2-28. 在一个布袋中装着只有颜色不同,其它都相同的红、白两种小球各一个,从中任意摸出一个球,记下颜色后放回并搅匀,再摸出一个球,则两次所摸出的球都是同一颜色球的概率是( )A、 B、 C、 D、9. 用一个半圆围成一个圆锥的侧面,圆锥的底面圆的半径为3,则该圆锥的母线长为( )A、3 B、6 C、9 D、1210. 关于抛物线y1=(1+x)2与y2=(1-x)2 , 下列说法错误的是( )A、图象y1与y2的开口方向相同 B、y1与y2的图象关于y轴对称 C、图象y2向左平移2个单位可得到y1的图象 D、图象y1绕原点旋转180°可得到y2的图象11. 如图,四边形ABCD是⊙O的内接四边形,若∠A=90o , ∠B=60o , AB=2,CD=1,则BC的长为( )
A、30° B、32° C、36° D、40°7. 将抛物线y=(x+2)2先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的表达式为( )A、y=(x+3)2-2 B、y=(x+3)2+2 C、y=(x+1)2+2 D、y=(x+1)2-28. 在一个布袋中装着只有颜色不同,其它都相同的红、白两种小球各一个,从中任意摸出一个球,记下颜色后放回并搅匀,再摸出一个球,则两次所摸出的球都是同一颜色球的概率是( )A、 B、 C、 D、9. 用一个半圆围成一个圆锥的侧面,圆锥的底面圆的半径为3,则该圆锥的母线长为( )A、3 B、6 C、9 D、1210. 关于抛物线y1=(1+x)2与y2=(1-x)2 , 下列说法错误的是( )A、图象y1与y2的开口方向相同 B、y1与y2的图象关于y轴对称 C、图象y2向左平移2个单位可得到y1的图象 D、图象y1绕原点旋转180°可得到y2的图象11. 如图,四边形ABCD是⊙O的内接四边形,若∠A=90o , ∠B=60o , AB=2,CD=1,则BC的长为( )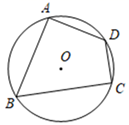 A、2 -2 B、4- C、2 D、312. 如图,抛物线y=ax2+bx+c的对称轴为直线x=1,下列结论①ac<0;②b2﹣4ac>0;③2a﹣b=0;④3a+c=0,其中,正确的个数是( )
A、2 -2 B、4- C、2 D、312. 如图,抛物线y=ax2+bx+c的对称轴为直线x=1,下列结论①ac<0;②b2﹣4ac>0;③2a﹣b=0;④3a+c=0,其中,正确的个数是( )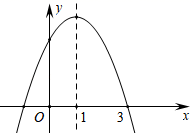 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 抛掷一枚质地均匀的硬币,若第一次是正面朝上,则第二次正面朝上的概率为 .14. 如图,在平面直角坐标系中,点A是函数y= (x>0)图象上的点,过点A作x轴的垂线交x轴于点B,点C在y轴上,若 ABC的面积为4,则k的值是 .
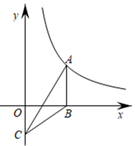 15. 如图,在Rt ABC中,∠C=90°,D为边AC上一点,∠A=∠CBD,若AC=8cm,cos∠CBD= ,则边AB=cm.
15. 如图,在Rt ABC中,∠C=90°,D为边AC上一点,∠A=∠CBD,若AC=8cm,cos∠CBD= ,则边AB=cm.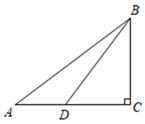 16. 在⊙O中,半径为4,弦AB的长为 ,弦AB所对的圆周角的度数为 .17. 如图,四边形ABCD是矩形,AB=2,AD= ,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是 .
16. 在⊙O中,半径为4,弦AB的长为 ,弦AB所对的圆周角的度数为 .17. 如图,四边形ABCD是矩形,AB=2,AD= ,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是 .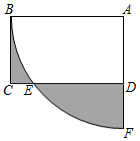 18. 如图,抛物线y= x2﹣3与x轴交于A、B两点,P是以点C(0,4)为圆心,3为半径的圆上的动点,M是线段PA的中点,连接OM.则线段OM的最大值是 .
18. 如图,抛物线y= x2﹣3与x轴交于A、B两点,P是以点C(0,4)为圆心,3为半径的圆上的动点,M是线段PA的中点,连接OM.则线段OM的最大值是 .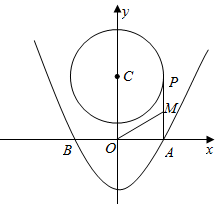
三、解答题
-
19. 计算:20. 一次函数y=- 的图象与反比例函数y= (x<0)的图象在第二象限交于点A(m,2)
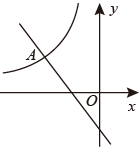 (1)、求反比例函数的表达式;(2)、根据图象直接写出不等式- < 的解集.21. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡P在线段DE上.
(1)、求反比例函数的表达式;(2)、根据图象直接写出不等式- < 的解集.21. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡P在线段DE上.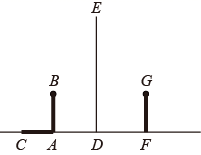 (1)、请你确定灯泡P所在的位置,并画出小亮在灯光下形成的影子.(2)、如果小明的身高AB=1.8m,他的影子长AC=1.5m,且他到路灯的距离AD=2m,求灯泡P距地面的高度.22. 把算珠放在计数器的3根插棒上可以构成一个数,例如,如图摆放的算珠表示数210.现将两颗算珠任意摆放在这3根插棒上,先放一颗算珠,再放另一颗,请用列表或画树状图的方法,求构成的数是三位数的概率.
(1)、请你确定灯泡P所在的位置,并画出小亮在灯光下形成的影子.(2)、如果小明的身高AB=1.8m,他的影子长AC=1.5m,且他到路灯的距离AD=2m,求灯泡P距地面的高度.22. 把算珠放在计数器的3根插棒上可以构成一个数,例如,如图摆放的算珠表示数210.现将两颗算珠任意摆放在这3根插棒上,先放一颗算珠,再放另一颗,请用列表或画树状图的方法,求构成的数是三位数的概率. 23. 图1是电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度,研究表明:如图2,当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个 俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时,观看屏幕最舒适,此时测得 ,液晶显示屏的宽AB为 .
23. 图1是电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度,研究表明:如图2,当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个 俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时,观看屏幕最舒适,此时测得 ,液晶显示屏的宽AB为 .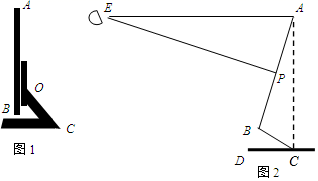 (1)、求眼睛E与显示屏顶端A的水平距离AE;(结果精确到 )(2)、求显示屏项端A与底座C的距离AC.(结果精确到 )(参考数据: )24. 某商场购进一种单价为10元的商品,根据市场调查发现:如果以单价20元售出,那么每天可卖出30个,每降价1元,每天可多卖出5个,若每个降价x(元),每天销售y(个),每天获得利润W(元).(1)、写出y与x的函数关系式;(2)、求W与x的函数关系式(不必写出x的取值范围)(3)、若降价x元(x不低于4元)时,销售这种商品每天获得的利润最大为多少元?25. 如图,点O是Rt ABC的斜边AB上一点,⊙O与边AB交于点A,D,与AC交于点E,点F是弧DE的中点,边BC经过点F,连接AF.
(1)、求眼睛E与显示屏顶端A的水平距离AE;(结果精确到 )(2)、求显示屏项端A与底座C的距离AC.(结果精确到 )(参考数据: )24. 某商场购进一种单价为10元的商品,根据市场调查发现:如果以单价20元售出,那么每天可卖出30个,每降价1元,每天可多卖出5个,若每个降价x(元),每天销售y(个),每天获得利润W(元).(1)、写出y与x的函数关系式;(2)、求W与x的函数关系式(不必写出x的取值范围)(3)、若降价x元(x不低于4元)时,销售这种商品每天获得的利润最大为多少元?25. 如图,点O是Rt ABC的斜边AB上一点,⊙O与边AB交于点A,D,与AC交于点E,点F是弧DE的中点,边BC经过点F,连接AF.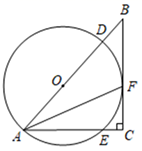 (1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为5,AF=8,求AC的长.26. 如图,直线y= 与x轴,y轴分别交于A,C两点,二次函数 的图象与x轴交于点B,且AC=BC,点D为该二次函数图象上一点,四边形ABCD为平行四边形.
(1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为5,AF=8,求AC的长.26. 如图,直线y= 与x轴,y轴分别交于A,C两点,二次函数 的图象与x轴交于点B,且AC=BC,点D为该二次函数图象上一点,四边形ABCD为平行四边形.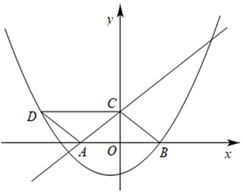 (1)、求该二次函数的表达式;(2)、动点M沿线段CD从C到D,同时动点N沿线段AC从A到C都以每秒1个单位长度的速度运动,设运动时间为t秒.
(1)、求该二次函数的表达式;(2)、动点M沿线段CD从C到D,同时动点N沿线段AC从A到C都以每秒1个单位长度的速度运动,设运动时间为t秒.①当点M运动过程中能否存在MN⊥AC?如果存在,请求出t的值;如果不存在,请说明理由;
②当点M运动到何处时,四边形ADMN的面积最小?并求出其最小面积.