山东省烟台市莱阳市2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 一天下午，小明先参加了校运动会男子 $200 m$ 比赛，过一段时间又参加了男生 $400 m$ 比赛，如图是摄影师在同一位置拍摄了他参加这两场比赛的照片，那么下列说法正确的是（）

A、乙照片是参加 $200 m$ 的 B、甲照片是参加 $200 m$ C、乙照片是参加 $400 m$ 的 D、无法判断甲、乙两张照片

查看试题解析
2. 如图是由若干个完全相同的小正方体组合而成的几何体，若将小正方体①移动到小正方体②的正上方，下列关于移动后几何体的三视图说法正确的是（）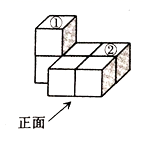

A、左视图发生变化 B、俯视图发生变化 C、主视图发生改变 D、左视图、俯视图和主视图都发生改变

查看试题解析
3. 如图，函数 $y_{1} = x + 1$ 与函数 $y_{2} = \frac{2}{x}$ 的图象相交于点 $M (m ， 2)$ ， $N (n ， - 1)$ ．若 $y_{1} > y_{2}$ ，则x的取值范围是（）

A、 $x < - 2$ 或 $0 < x < 1$ B、 $x < - 2$ 或 $x > 1$ C、 $- 2 < x < 0$ 或 $0 < x < 1$ D、 $- 2 < x < 0$ 或 $x > 1$

查看试题解析
4. 已知关于 $x$ 的一元二次方程 $x^{2} + 4 x - k = 0$ ，当 $- 4 < k < 0$ 时，该方程解的情况是（）

A、有两个不相等的实数根 B、没实数根 C、有两个相等的实数根 D、不能确定

查看试题解析
5. 如图， $∠ E F G = 90 ° ， E F = 10 ， O G = 17 ， \cos ∠ F G O = \frac{3}{5}$ ，则点 $F$ 的坐标是（）

A、 $(8 ， \frac{27}{4})$ B、 $(8 ， 12)$ C、 $(6 ， \frac{33}{4})$ D、 $(6 ， 10)$

查看试题解析
6. 如图， $A B$ 是 $⊙ O$ 的直径， $C D$ 是 $⊙ O$ 的弦， $∠ A C D = 30 ° ， A D = \sqrt{3}$ ，下列说法错误的是（）

A、 $∠ B = 30 °$ B、 $∠ B A D = 60 °$ C、 $B D = 2 \sqrt{3}$ D、 $A B = 2 \sqrt{3}$

查看试题解析
7. 如图，A、B分别是反比例函数 $y = \frac{4}{x} (x > 0)$ 图象上的两点，连结 $O A$ 、 $O B$ ，分别过点A、B作x轴的垂线，垂足分别为C、E，且 $A C$ 交 $O B$ 于点D，若 $S_{Δ O A D} = \frac{4}{3}$ ，则 $\frac{C D}{B E}$ 的值为（）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
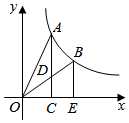8. 二次函数 $y = a x^{2} - 2 a x + b$ 中，当 $- 1 \leq x \leq 4$ 时， $- 2 \leq y \leq 3$ ，则 $b - a$ 的值为（）

A、-6 B、-6或7 C、3 D、3或-2

查看试题解析
9. 如图，在国旗台DF上有一根旗杆AF ，国庆节当天小明参加升旗仪式，在B处测得旗杆顶端的仰角为37°，小明向前走4米到达点E ，经过坡度为1的坡面DE ，坡面的水平距离是1米，到达点D ，测得此时旗杆顶端的仰角为53°，则旗杆的高度约为（）米．（参考数据： $\sin 37 ° \approx 0.6$ ， $\cos 37 ° \approx 0.8$ ， $\tan 37 ° \approx 0.75$ ）

A、6.29 B、4.71 C、4 D、5.33

查看试题解析
10. 记某商品销售单价为x元，商家销售此种商品每月获得的销售利润为y元，且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时，他每月均可获得销售利润1800元；当商家将此种商品销售单价定为80元时，他每月可获得销售利润1550元，则y与x的函数关系式是（）

A、y＝﹣（x﹣60）²+1825 B、y＝﹣2（x﹣60）²+1850 C、y＝﹣（x﹣65）²+1900 D、y＝﹣2（x﹣65）²+2000

查看试题解析
11. 如图， $A 、 B 、 C 、 D$ 是 $⊙ O$ 上的点， $∠ A O D + ∠ B O C = 180 °$ ．若 $A D = 2 ， B C = 6$ ，则 $Δ B O C$ 的面积为（）

A、3 B、6 C、9 D、12

查看试题解析
12. 如图，将矩形ABCD绕着点A逆时针旋转得到矩形AEFG，点B的对应点E落在边CD上，且DE=EF，若AD=3 $\sqrt{3}$ ，则 $\overset{⌢}{C F}$ 的长为（）

A、 $\frac{9}{4}$ π B、 $\frac{3}{4}$ π C、 $\frac{\sqrt{6}}{4}$ π D、π

查看试题解析

二、填空题

13. 如图，在 $4 \times 5$ 的正方形网格中，每个小正方形的边长都是1， $Δ A B C$ 的顶点都在这些小正方形的顶点上，那么 $\cos ∠ A C B$ 值为．

查看试题解析
14. 如图，点A在反比例函数 $y = \frac{k}{x}$ （x>0）图象上，AB⊥x轴于点B，点C在x轴负半轴上，且BO=2CO，若△ABC的面积为18，则k的值为．

查看试题解析
15. 抛物线 $y = a x^{2} - 2 a x + 1$ 交y轴于点M，点M关于其对称轴的对称点N的坐标为.

查看试题解析
16. 如图， $E B$ 为驾驶员的盲区，驾驶员的眼睛点 $P$ 处与地面 $B E$ 的距离为1.6米，车头 $F A C D$ 近似看成一个矩形，且满足 $3 F D = 2 F A$ ，若盲区 $E B$ 的长度是6米，则车宽 $F A$ 的长度为米．

查看试题解析
17. 边长为6的正三角形的外接圆的周长为．

查看试题解析
18. 如图，菱形 $A B C D$ 的边长为10，面积为80， $∠ B A D < 90 °$ ，⊙O与边 $A B$ ， $A D$ 都相切，菱形的顶点A到圆心O的距离为5，则⊙O的半径长等于．

查看试题解析

三、解答题

19. 如图，一次函数 $y = m x + n (m \neq 0)$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于第一、三象限内的 $A 、 B$ 两点，与 $y$ 轴交于点 $C$ ，过点 $B$ 作 $B M ⊥ x$ 轴，垂足为 $M$ ， $B M = O M$ ， $O B = 2 \sqrt{2}$ ，点 $A$ 的纵坐标为4

(1)、求反比例函数和一次函数的表达式；

(2)、求 $Δ B O C$ 的面积．

查看试题解析
20. 如图， $A B$ 是半圆 $O$ 的直径， $C ， D$ 是半圆 $O$ 上不同于 $A ， B$ 的两点， $A C$ 平分 $∠ D A B$ ， $A C$ 与 $B D$ 相交于点 $F$ ，延长 $A C$ 到点 $E$ ，使 $C E = C F$ ．

(1)、求证： $B E$ 是 $⊙ O$ 的切线；

(2)、若 $B C = A D = 6$ ，求 $⊙ O$ 的半径．

查看试题解析
21. 如图，实践小组为了测量塔 $A B$ 的高度，先从与塔底中心 $B$ 在同一水平面上的点 $D$ 出发，沿着坡度为1：0.75的斜坡 $D E$ 行走10米至坡顶 $E$ 处，再从 $E$ 处沿水平方向继续前行若干米后至点 $F$ 处，在 $F$ 点测得塔顶 $A$ 的仰角为63°，塔底 $C$ 的俯角为45°， $B$ 与 $C$ 的水平距离为4米（图中 $A 、 B 、 C 、 D 、 E 、 F$ 在同一平面内， $E 、 F$ 和 $D 、 C 、 B$ 分别在同一水平线上），根据测量数据，求塔 $A B$ 的高度．（计算结果精确到0.1米，参考数据： $\sin 63 ° \approx 0.89 ， \cos 63 ° \approx 0.45 ， \tan 63 ° \approx 1.96$ ）

查看试题解析
22. 网络销售已经成为一种热门的销售方式，某公司在某网络平台上进行直播销售板栗.已知板栗的成本价格为6元/ $k g$ ，每日销售量 $y (k g)$ 与销售单价 $x$ （元/ $k g$ ）满足一次函数关系，下表记录的是有关数据.经销售发现，销售单价不低于成本价且不高于30元/ $k g$ .设公司销售板栗的日获利为 $w$ （元）.

$x$ （元/ $k g$ ）

7

8

9

$y (k g)$

4300

4200

4100

(1)、请求出日销售量 $y$ 与销售单价 $x$ 之间的函数关系式；

(2)、当销售单价定为多少时，销售这种板栗日获利 $w$ 最大？最大利润为多少元？

(3)、当销售单价在什么范围内时，日获利 $w$ 不低于42000元？

查看试题解析
23. 如图，AB为⊙O的直径，射线AD交⊙O于点F，点C为劣弧 $\overset{⌢}{B F}$ 的中点，CE为⊙O的切线交AD于点E，连接AC．

(1)、求证：CE⊥AD；

(2)、若∠BAC＝30°，AB＝4，求阴影部分的面积．

查看试题解析
24. 如图，在平面直角坐标系中，点 $A (2 ， 3)$ 为二次函数 $y = a x^{2} + b x - 2 (a \neq 0)$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限的交点，已知该抛物线 $y = a x^{2} + b x - 2 (a \neq 0)$ 与 $x$ 轴正、负半轴分别交于点 $E$ 、点 $D$ ，交 $y$ 轴负半轴于点 $B$ ，且 $\tan ∠ A D E = \frac{1}{2}$ ．

(1)、求二次函数和反比例函数的表达式；

(2)、已知点 $M$ 为抛物线上一点，且在第三象限，顺次连接点 $D 、 M 、 B 、 E$ ，求四边形 $D M B E$ 面积的最大值．

查看试题解析
25. 跳绳时，绳甩到最高处时的形状是抛物线，正在甩绳的甲、乙两名同学拿绳的手间距 $A B$ 为6米，到地面的距离 $A O$ 和 $B D$ 均为0.9米，身高为1.4米的小丽站在距点 $O$ 的水平距离为1米的点 $F$ 处，绳子甩到最高处时刚好通过她的头顶点 $E$ ．以点 $O$ 为原点建立如图所示的平面直角坐标系，设此抛物线的解析式为 $y = a x^{2} + b x + 0.9$ ．

(1)、求该抛物线的表达式；

(2)、如果小明站在 $O D$ 之间，且离点 $O$ 的距离为3米，当绳子甩到最高处时刚好通过他的头顶上方0.4米处，求小明的身高是多少？此时小明若向点 $O$ 方向走多少米，就能让绳子甩到最高处时，绳子刚好通过他的头顶；

(3)、如果有若干个与小明同身高的同学一起站在 $O D$ 之间玩跳绳，现知只要绳子甩到最高处时超过她们的头顶且每个同学同方向站立时的脚跟之间距离不小于0.55米就可以一起玩，问最多可以几个同学一起玩．

查看试题解析

$x$ （元/ $k g$ ）	7	8	9
$y (k g)$	4300	4200	4100