山东省烟台蓬莱市(五四制)2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 下列说法中正确的是( )A、相等的圆心角所对的弧相等 B、相等的弧所对的圆心角相等 C、相等的弦所对的弦心距相等 D、弦心距相等,则弦相等2. 一斜坡的坡度是 ,则此斜坡的坡角是( )A、15º B、30º C、45º D、60º3. 函数的自变量x满足 ≤x≤2时,函数值y满足 ≤y≤1,则这个函数可以是( )A、y= B、y= C、y= D、y=4. 一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A、1米 B、5米 C、6米 D、7米5. 正方形网格中,∠AOB如图放置,则cos∠AOB的值为( )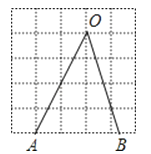 A、 B、 C、 D、6. 如图,点 在双曲线 上,点 在双曲线 上,且 轴, 、 在 轴上,若四边形 为矩形,则它的面积为( )
A、 B、 C、 D、6. 如图,点 在双曲线 上,点 在双曲线 上,且 轴, 、 在 轴上,若四边形 为矩形,则它的面积为( )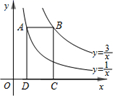 A、1 B、2 C、3 D、47. 点 均在二次函数 的图象上,则 的大小关系是( )A、 B、 C、 D、8. 如图, 为⊙ 的直径, 为半圆的中点,动点 从点 出发在圆周上顺时针匀速运动,到达点 后停止运动,在点 运动过程中(不包括 、 两点), 的值( )
A、1 B、2 C、3 D、47. 点 均在二次函数 的图象上,则 的大小关系是( )A、 B、 C、 D、8. 如图, 为⊙ 的直径, 为半圆的中点,动点 从点 出发在圆周上顺时针匀速运动,到达点 后停止运动,在点 运动过程中(不包括 、 两点), 的值( ) A、由小逐渐增大 B、固定不变为45° C、由大逐渐减小 D、固定不变为60°9. 连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
A、由小逐渐增大 B、固定不变为45° C、由大逐渐减小 D、固定不变为60°9. 连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( ) A、四边形 与四边形 的面积相等 B、连接 ,则 分别平分 和 C、整个图形是轴对称图形,但不是中心对称图形 D、 是等边三角形10. 若点 , 在反比例函数 的图象上,且 ,则a的取值范围是( )A、 B、 C、 D、 或11. 如图,将边长为3的正方形铁丝框ABCD,变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为( )
A、四边形 与四边形 的面积相等 B、连接 ,则 分别平分 和 C、整个图形是轴对称图形,但不是中心对称图形 D、 是等边三角形10. 若点 , 在反比例函数 的图象上,且 ,则a的取值范围是( )A、 B、 C、 D、 或11. 如图,将边长为3的正方形铁丝框ABCD,变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为( ) A、3 B、6 C、9 D、3π12. 如图,二次函数 的图象与x油交于A、B两点,与y轴交于点C,对称轴为直线 ,点B的坐标为 ,则下列结论:①线段 ;② ;③ ;④ .其中正确的结论是( )
A、3 B、6 C、9 D、3π12. 如图,二次函数 的图象与x油交于A、B两点,与y轴交于点C,对称轴为直线 ,点B的坐标为 ,则下列结论:①线段 ;② ;③ ;④ .其中正确的结论是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 如图, 中, , , ,则 的面积是 .
 14. 已知抛物线 与x轴一个交点的坐标为 ,则一元二次方程 的根为 .15. 如图,直线 与 相切于点 , 、 是 的两条弦,且 .若 的半径为5, ,则弦 的长为 .
14. 已知抛物线 与x轴一个交点的坐标为 ,则一元二次方程 的根为 .15. 如图,直线 与 相切于点 , 、 是 的两条弦,且 .若 的半径为5, ,则弦 的长为 . 16. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
16. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 . 17. 如图,在 中, ,过点A,C的圆的圆心在边 上,点M是优弧 (不与点A,C重合)上的一点,则 .
17. 如图,在 中, ,过点A,C的圆的圆心在边 上,点M是优弧 (不与点A,C重合)上的一点,则 . 18. 如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1 , A2…An﹣1为OA的n等分点,点B1 , B2…Bn﹣1为CB的n等分点,连结A1B1 , A2B2 , …An﹣1Bn﹣1 , 分别交曲线 (x>0)于点C1 , C2 , …,Cn﹣1 . 若C15B15=16C15A15 , 则n的值为 . (n为正整数)
18. 如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1 , A2…An﹣1为OA的n等分点,点B1 , B2…Bn﹣1为CB的n等分点,连结A1B1 , A2B2 , …An﹣1Bn﹣1 , 分别交曲线 (x>0)于点C1 , C2 , …,Cn﹣1 . 若C15B15=16C15A15 , 则n的值为 . (n为正整数)
三、解答题
-
19. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=
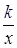 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3). 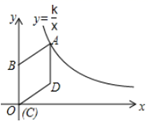 (1)、求k的值;(2)、若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=
(1)、求k的值;(2)、若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=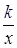 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离. 20. 从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是;(2)、若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.21. 根据图中所给信息,解出下图中未知数 、 的值.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离. 20. 从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是;(2)、若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.21. 根据图中所给信息,解出下图中未知数 、 的值. 22. 如图,小明站在河岸上的点G处看见河里有一只小船C沿垂直于岸边的方向划过来,此时,测得小船C的俯角是 ,若小明的眼睛与地面的距离是 , , 平行于 ,迎水坡的坡度 ,坡长 ,求小船C到岸边的距离 的长.(参考数据: ,结果保留一位小数)
22. 如图,小明站在河岸上的点G处看见河里有一只小船C沿垂直于岸边的方向划过来,此时,测得小船C的俯角是 ,若小明的眼睛与地面的距离是 , , 平行于 ,迎水坡的坡度 ,坡长 ,求小船C到岸边的距离 的长.(参考数据: ,结果保留一位小数)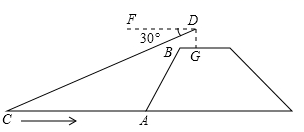 23. 某公司计划投资 、 两种产品,若只投资 产品,所获得利润 (万元)与投资金额 (万元)之间的关系如图所示,若只投资 产品,所获得利润 (万元)与投资金额 (万元)的函数关系式为 .
23. 某公司计划投资 、 两种产品,若只投资 产品,所获得利润 (万元)与投资金额 (万元)之间的关系如图所示,若只投资 产品,所获得利润 (万元)与投资金额 (万元)的函数关系式为 .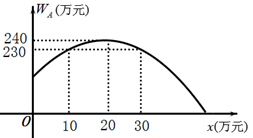 (1)、求 与 之间的函数关系式;(2)、若投资 产品所获得利润的最大值比投资 产品所获得利润的最大值少140万元,求 的值;(3)、该公司筹集 万元资金,同时投资 、 两种产品,设投资 产品的资金为 万元,所获得的总利润记作 万元,若 时, 随 的增大而减少,求 的取值范围.24. 如图,△ABC内接于⊙O,AB是直径,过点A作直线MN,且∠MAC=∠ABC.
(1)、求 与 之间的函数关系式;(2)、若投资 产品所获得利润的最大值比投资 产品所获得利润的最大值少140万元,求 的值;(3)、该公司筹集 万元资金,同时投资 、 两种产品,设投资 产品的资金为 万元,所获得的总利润记作 万元,若 时, 随 的增大而减少,求 的取值范围.24. 如图,△ABC内接于⊙O,AB是直径,过点A作直线MN,且∠MAC=∠ABC.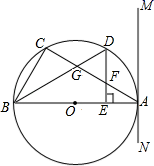 (1)、求证:MN是⊙O的切线.(2)、设D是弧AC的中点,连结BD交AC于点G,过点D作DE⊥AB于点E,交AC于点F.
(1)、求证:MN是⊙O的切线.(2)、设D是弧AC的中点,连结BD交AC于点G,过点D作DE⊥AB于点E,交AC于点F.①求证:FD=FG.
②若BC=3,AB=5,试求AE的长.
25. 如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C. (1)、求抛物线的解析式;(2)、若直线y=kx+t经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;(3)、点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若直线y=kx+t经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;(3)、点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切?若存在,请求出点P的坐标;若不存在,请说明理由.