山东省潍坊市诸城市2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中，自变量 $x$ 的取值范围是 $x \geq 2021$ 的函数是（）

A、 $y = 1 - 2021 x$ B、 $y = \sqrt{2021 - x}$ C、 $y = \sqrt{x - 2021}$ D、 $y = \frac{1}{x - 2021}$

查看试题解析
2. 一元二次方程 $x {}^{2}- 2 x + 3 = 0$ 根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、只有一个实数根

查看试题解析
3. 若点 $(- 6 ， y_{1})$ ， $(2 ， y_{2})$ ， $(3 ， y_{3})$ 都是反比例函数 $y = \frac{a^{2} + 1}{x}$ 图象上的点，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 大小关系是（）

A、 $y_{1} < y_{3} < y_{2}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{1} < y_{2} < y_{3}$

查看试题解析
4. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ，延长 $A O$ 交 $⊙ O$ 于点 $B$ ，连接 $B E$ .若 $∠ C = 100 °$ ， $∠ D A E = 50 °$ ，则 $∠ E$ 的度数为（）

A、50° B、60° C、70° D、80°

查看试题解析
5. 等腰三角形的底边长为6，腰长是方程 $x^{2} - 8 x + 15 = 0$ 的一个根，则该等腰三角形的周长为（）

A、12 B、16 C、l2或16 D、15

查看试题解析
6. 如图，是一次函数y=kx+b的图象，则二次函数y=2kx²﹣bx+1的图象大致为（）

A、 B、 C、 D、

查看试题解析
7. 如图，AB是 $⊙ O$ 的直径， $⊙ O$ 的半径为2，AD为正十边形的一边，且 $A D / / O C$ ，则劣弧BC的长为（）

A、 $π$ B、 $\frac{3}{2} π$ C、 $\frac{4}{3} π$ D、 $\frac{6}{5} π$

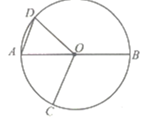查看试题解析
8. 如图，在 $x$ 轴正半轴上依次截取 $O A_{1} = A_{1} A_{2} = A_{2} A_{3} = \dots = A_{2020} A_{2021}$ ，过点 $A_{1}$ ． $A_{2}$ ， $A_{3}$ 、 $\dots$ 、 $A_{2020}$ 、 $A_{2021}$ 分别作 $x$ 轴的垂线，与反比例函数 $y = \frac{2}{x}$ 的图象依次相交于 $P_{1}$ ， $P_{2}$ 、 $P_{3}$ 、 $\dots$ 、 $P_{2021}$ ，得到 $Δ O P_{1} A_{1}$ 、 $Δ O_{1} P_{2} A_{2}$ 、 $\dots$ 、 $Δ A_{2020} P_{2021} A_{2021}$ ，并设其面积分别为 $S_{1}$ 、 $S_{2}$ 、 $\dots$ 、 $S_{2021}$ ，则 $S_{2021}$ 的值为（）

A、 $\frac{1}{2021}$ B、 $\frac{1}{2020}$ C、 $\frac{2}{2021}$ D、 $\frac{1}{1010}$

查看试题解析
9. 已知正比例函数 $y = k_{1} x$ 和反比例函数 $y = \frac{k_{2}}{x}$ ，在同一直角坐标系下的图象如图所示，其中满足 $k_{1} \cdot k_{2} > 0$ 且 $k_{1} < 0$ 的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在 $△ A B C$ 中， $D E / / B C$ ， $A D ： D B = 1 ： 2$ ， $D E = 2$ ，则下列结论错误的是（）

A、 $B C = 6$ B、 $\frac{A E}{E C} = \frac{1}{2}$ C、 $\frac{S_{△ A D E}}{S_{△ A B C}} = \frac{1}{4}$ D、 $△ A D E ∽ △ A B C$

查看试题解析
11. 如图， $A B$ 、 $C D$ 是 $⊙ O$ 的两条弦，且 $A B = C D$ ． $O M ⊥ A B$ ， $O N ⊥ C D$ ，垂足分别为点 $M$ 、 $N$ ， $B A$ 、 $D C$ 的延长线交于点 $P$ ，连接 $O P$ ．下列结论正确的个数是（）
① $\overset{⌢}{A B} = \overset{⌢}{C D}$ ；② $O M = O N$ ；③ $P A = P C$ ；④ $∠ B P O = ∠ D P O$

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 已知二次函数 $y = a x^{2} + b x + c$ 与自变量 $x$ 的部分对应值如表所示，下列结论正确的是（）

$x$

$\dots$

-1

0

1

3

$\dots$

$y$

$\dots$

-3

1

3

1

$\dots$

A、 $a > 0$ B、方程 $a x^{2} + b x + c = - 2$ 的正根在4和5之间 C、 $2 a + b < 0$ D、若点 $(5 ， y_{1})$ ， $(- \frac{2}{3} ， y_{2})$ 都在函数图象上，则 $y_{1} < y_{2}$

查看试题解析

二、填空题

13. 已知α是锐角，2sinα- $\sqrt{2}$ =0，则α=.

查看试题解析
14. 若抛物线y=ax²+bx+c的顶点是A（2，1），且经过点B（1，0），则抛物线的函数关系式为.

查看试题解析
15. 如图， $Δ A B C$ 的顶点都是正方形网格中的格点，则 $\cos ∠ C A B =$ ．

查看试题解析
16. 将抛物线 $y = x^{2} - 6 x + 10$ 先向左平移2个单位长度，再向下平移1个单位长度，得到的抛物线与 $x$ 轴的交点坐标是．

查看试题解析
17. 如图，是一个长为30m，宽为20m的矩形花园，现要在花园中修建等宽的小道，剩余的地方种植花草．如图所示，要使种植花草的面积为532m² ，那么小道进出口的宽度应为米．

查看试题解析
18. 如图，在 $Δ A B C$ 中， $B C = 120$ ，高 $A D = 60$ ，正方形 $E F G H$ 一边在 $B C$ 上，点 $E$ ， $F$ 分别在 $A B$ ， $A C$ 上， $A D$ 交 $E F$ 于点 $N$ ，则 $A N$ 的长为．

查看试题解析

三、解答题

19. 解下列方程：

(1)、 $x^{2} - 4 x - 1 = 0$

(2)、 $3 {(x - 1)}^{2} = 2 (x - 1)$

查看试题解析
20. 如图，一次函数 $y = k x + b$ 的图象交反比例函数 $y = \frac{a}{x} (x > 0)$ 的图象于 $A (2 ， - 4) ， B (m ， - 1)$ 两点，交 $x$ 轴于点 $C$ ．

(1)、求反比例函数与一次函数的关系式．

(2)、求 $Δ A B O$ 的面积．

(3)、根据图象回答：当 $x$ 为何值时，一次函数的值大于反比例函数的值？

查看试题解析
21. 如图，某中学依山而建，校门 $A$ 处有一坡度 $i = 5 ： 12$ 的斜坡 $A B$ ，长度为13米，在坡顶 $B$ 处看教学楼 $C F$ 的楼顶 $C$ 的仰角 $∠ C B F = 45^{°}$ ，离 $B$ 点4米远的 $E$ 处有一个花台，在 $E$ 处仰望 $C$ 的仰角是 $∠ C E F = 60^{°}$ ， $C F$ 的延长线交校门处的水平面于点 $D$ ．(提示： $\frac{1}{\sqrt{3} - 1} = \frac{\sqrt{3} + 1}{(\sqrt{3} - 1) (\sqrt{3} + 1)} = \frac{\sqrt{3} + 1}{2}$ )

(1)、求坡顶 $B$ 的高度；

(2)、求楼顶 $C$ 的高度 $C D$ ．

查看试题解析
22. 某超市经销一种商品，成本价为50元/千克．规定每千克售价不低于成本价，且不高于85元，经市场调查发现，该种商品每天销售量 $y$ (千克)与销售单价 $x$ (元/千克)满足一次函数关系，部分数据如下表所示：

销售单价 $x$ (元/千克)

55

65

75

销售量 $y$ (千克)

110

90

70

(1)、求 $y$ (千克)与 $x$ (元/千克)之间的函数表达式并注明自变量的取值范围；

(2)、为保证某天获得10000元的销售利润，则该天的销售单价应定为多少元?

(3)、当销售单价定为多少时，才能使当天的销售利润最大?最大利润是多少?

查看试题解析
23. 如图，AB为⊙O的直径，C为⊙O上一点，∠ABC的角平分线交⊙O于点D.过点D作DE⊥BC，交BC的延长线于点E.

(1)、试判断DE与⊙O的位置关系，并说明理由.

(2)、过点D作DF⊥AB于点F，连接CD，若CD=2，BD=2 $\sqrt{3}$ ，求图中阴影部分的面积.

查看试题解析
24. 如图，已知抛物线 $y = - x^{2} + b x + c$ 与一直线相交于 $A (- 1 ， 0)$ ， $C (2 ， 3)$ 两点，与 $y$ 轴交于点 $N$ ，其顶点为 $D$ ．

(1)、求抛物线的表达式；

(2)、若 $P$ 是抛物线上位于直线 $A C$ 上方的一个动点，求 $Δ A P C$ 的面积的最大值；

(3)、在抛物线对称轴上存在点 $M$ ，使得 $Δ A N M$ 是直角三角形，请直接写出点 $M$ 的坐标．

查看试题解析

销售单价 $x$ (元/千克)	55	65	75
销售量 $y$ (千克)	110	90	70

$x$	$\dots$	-1	0	1	3	$\dots$
$y$	$\dots$	-3	1	3	1	$\dots$