山东省潍坊市安丘市2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 如图,面积为1的等边三角形 中, 分别是 , , 的中点,则 的面积是( )
 A、1 B、 C、 D、2. 已知 ,运用科学计算器求锐角 时(在开机状态下),按下的第一个键是( )A、
A、1 B、 C、 D、2. 已知 ,运用科学计算器求锐角 时(在开机状态下),按下的第一个键是( )A、 B、
B、 C、
C、 D、
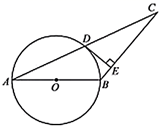
D、 3. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、4. 4.如图, 是 的外接圆 的直径,若 ,则 ( )
3. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、4. 4.如图, 是 的外接圆 的直径,若 ,则 ( ) A、30° B、40° C、50° D、60°5. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A、30° B、40° C、50° D、60°5. 如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )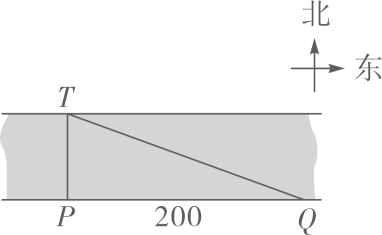 A、200tan70°米 B、 米 C、200sin70°米 D、 米6. 如图, 为 的切线,点 为切点, 交 于点 ,点 在 上,连接 ,若 ,则 的度数为( )
A、200tan70°米 B、 米 C、200sin70°米 D、 米6. 如图, 为 的切线,点 为切点, 交 于点 ,点 在 上,连接 ,若 ,则 的度数为( ) A、20° B、25° C、30° D、35°7. 定义运算: .例如: .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根8. 如图,点A是反比例函数y (x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y= 的图象于点B,点P是x轴上的动点,则△PAB的面积为( )
A、20° B、25° C、30° D、35°7. 定义运算: .例如: .则方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根8. 如图,点A是反比例函数y (x>0)上的一点,过点A作AC⊥y轴,垂足为点C,AC交反比例函数y= 的图象于点B,点P是x轴上的动点,则△PAB的面积为( )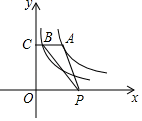 A、2 B、4 C、6 D、89. 下列命题是真命题的是( )A、相等的圆心角所对的弧相等 B、相等的圆心角所对的两条弦相等 C、弦的垂直平分线经过圆心 D、长度相等的弧的度数相等10. 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )
A、2 B、4 C、6 D、89. 下列命题是真命题的是( )A、相等的圆心角所对的弧相等 B、相等的圆心角所对的两条弦相等 C、弦的垂直平分线经过圆心 D、长度相等的弧的度数相等10. 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )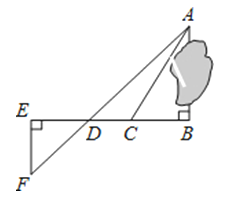 A、BC,∠ACB B、DE,DC,BC C、EF,DE,BD D、CD,∠ACB,∠ADB11. 如图,已知二次函数 的图象与轴相交于 两点.则以下结论正确的有( )个.① ② ③ ④
A、BC,∠ACB B、DE,DC,BC C、EF,DE,BD D、CD,∠ACB,∠ADB11. 如图,已知二次函数 的图象与轴相交于 两点.则以下结论正确的有( )个.① ② ③ ④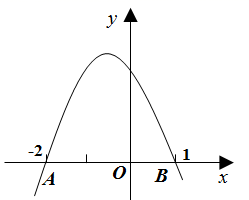 A、0 B、1 C、2 D、312. 如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
A、0 B、1 C、2 D、312. 如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( ) A、DC=DT B、AD= DT C、BD=BO D、2OC=5AC
A、DC=DT B、AD= DT C、BD=BO D、2OC=5AC二、填空题
-
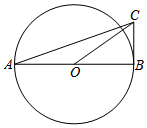
13. 请写出一个过点(1,1),且与x轴无交点的函数表达式 .14. 一个不透明的袋子里装有4个红球和2个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为 .15. 如图,已知AB是⊙O的直径,BC与⊙O相切于点B,连接AC,OC.若sin∠BAC= ,则tan∠BOC= .
 16. 在平面直角坐标系 中,直线 与双曲线 交于A,B两点.若点A,B的纵坐标分别为 ,则 的值为 .17. 如图4,我国现代数学著作《九章算术》中有“井深几何”问题如下:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?它的题意可以由如图所示获得,井深 为尺.
16. 在平面直角坐标系 中,直线 与双曲线 交于A,B两点.若点A,B的纵坐标分别为 ,则 的值为 .17. 如图4,我国现代数学著作《九章算术》中有“井深几何”问题如下:今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?它的题意可以由如图所示获得,井深 为尺. 18. 如图, 是 的直径,弦 ,垂足为点 .连接 ,如果 ,那么图中阴影部分的面积是
18. 如图, 是 的直径,弦 ,垂足为点 .连接 ,如果 ,那么图中阴影部分的面积是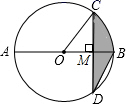
三、解答题
-
19. 已知关于x的一元二次方程 .(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两实根为 , ,且 ,求m的值.20. 在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
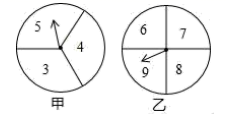 (1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、计算平局的概率.(3)、刘凯说:“这种规则不公平”,你认同他的说法吗?请说明理由.(4)、若你认为不公平,请你帮他们修改规则使游戏公平?21. 构建几何图形解决代数问题是“数形结合”思想的重要策略.在计算 时,如图,在 中, ,延长 使 ,连接 ,得 ,所以 ,类比这种方法,计算 (画图并写出过程)
(1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、计算平局的概率.(3)、刘凯说:“这种规则不公平”,你认同他的说法吗?请说明理由.(4)、若你认为不公平,请你帮他们修改规则使游戏公平?21. 构建几何图形解决代数问题是“数形结合”思想的重要策略.在计算 时,如图,在 中, ,延长 使 ,连接 ,得 ,所以 ,类比这种方法,计算 (画图并写出过程)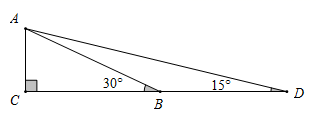 22. 如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.
22. 如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.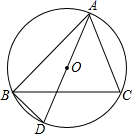 (1)、求证:∠CAD=∠ABC;(2)、若AD=6,求 的长.
(1)、求证:∠CAD=∠ABC;(2)、若AD=6,求 的长.