山东省泰安市宁阳县（五四制）2020-2021学年九年级上学期期末数学试题
试卷更新日期：2021-11-16 类型：期末考试
一、单选题
-
1. 点P（﹣1，3）在反比例函数y＝ （k≠0）的图象上，则k的值是（ ）A、 B、3 C、 D、﹣32. 抛物线y＝2（x+3）2+4的顶点坐标是（ ）A、（3，4） B、（﹣3，4） C、（3，﹣4） D、（2，4）3. 如图，在 中， ， ， ，则 等于（ ）
A、 B、 C、 D、4. 在Rt△ABC中，∠C＝90°，BC＝1，AC＝ ，那么∠B的度数是（ ）A、15° B、45° C、30° D、60°5. 抛物线y＝3x2向左平移4个单位，再向下平移2个单位，所得到的抛物线是（ ）A、y＝3（x﹣4）2+2 B、y＝3（x﹣4）2﹣2 C、y＝3（x+4）2﹣2 D、y＝3（x+4）2+26. 抛物线y＝x2﹣5x+6与x轴的交点情况是（ ）A、有两个交点 B、只有一个交点 C、没有交点 D、无法判断7. 如图， 的三点都在 上，AB是直径， ，则 为（ ）
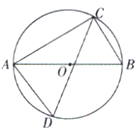A、 B、 C、 D、8. 如图，过反比例函数 的图象上一点 作 轴于点 ，连接 ，若 ，则 的值为（ ）
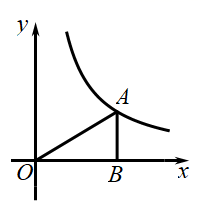A、3 B、4 C、5 D、69. 计算sin230°+cos260°的结果为（ ）A、 B、 C、1 D、10. 如图，A，B，P是半径为2的⊙O上的三点，∠APB＝45°，则弦AB的长为（ ）
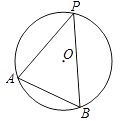A、2 B、4 C、 D、11. 已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc＜0；②b＞a+c；③2a-b=0；④b2-4ac＜0．其中正确的结论个数是（ ）
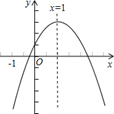A、1个 B、2个 C、3个 D、4个12. 如图，∠ACB=90°，CD是AB边上的高，若AD=24，BD=6，则CD的长是（ ）
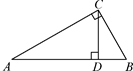A、8 B、10 C、12 D、14二、填空题
-
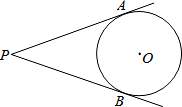
13. 已知扇形的圆心角为60°，半径为1，则扇形的弧长为14. 等腰直角三角形的直角边长为2，其外接圆的半径为 ．15. 如图所示，PA、PB是⊙O的切线，A、B为切点，∠APB=40°，点C是⊙O上不同于A、B的任意一点，则∠ACB的度数为.
16. 如图，圆锥底面半径为rcm，母线长为5cm，侧面展开图是圆心角为216°的扇形，则r为cm．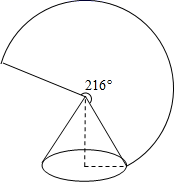
17. 如图，点A ， B ， C在圆O上，∠ACB＝54°，则∠ABO的度数是.
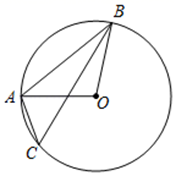18. 如图，AB是⊙O的弦，AC是⊙ 的切线，A为切点，BC经过圆心．若∠C=50°，则∠B的度数为 ．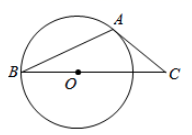
三、解答题
-
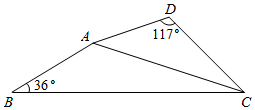
19. 如图，已知AD＝4cm，BC：AC＝3：2，∠B＝36°，∠D＝117°，△ABC∽△DAC，求AB的长和∠BAD的度数．
20. 如图，一次函数 ＝ax+b与反比例函数 ＝ 的图象相交于A（2，8），B（8，2）两点，连接AO，BO，延长AO交反比例函数图象于点C．
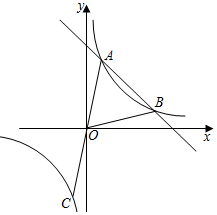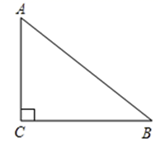
(1)、求一次函数 的表达式与反比例函数 的表达式；(2)、当 ＜ 时，直接写出自变量x的取值范围为；(3)、求 的值(4)、点P是x轴上一点，当 ＝ 时，请求出点P的坐标．21. 如图，点C、D在线段AB上，且△PCD是等边三角形．∠APB＝120°．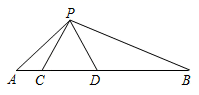
(1)、求证：△ACP∽△PDB；(2)、当AC＝4，BD＝9时，试求CD的值．22. 如图，把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案，求∠ACF，∠AFC的度数．
