山东省泰安市岱岳区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 如图所示的几何体是由几个大小相同的小正方体搭成的,其俯视图是( )
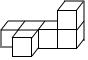 A、
A、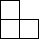 B、
B、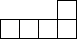 C、
C、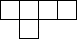 D、
D、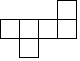 2. 点 在反比例函数 的图像上,则( )A、 B、 C、 D、3. 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
2. 点 在反比例函数 的图像上,则( )A、 B、 C、 D、3. 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )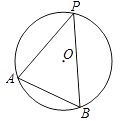 A、2 B、4 C、 D、4. 如图,▱ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A、2 B、4 C、 D、4. 如图,▱ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )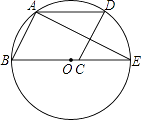 A、36° B、46° C、27° D、63°5. 抛物线 的顶点坐标是( )A、 B、 C、 D、6. 如图,已知 内接于 是 的直径, 与 相切,切点为 ,若 ,则 ( )度.
A、36° B、46° C、27° D、63°5. 抛物线 的顶点坐标是( )A、 B、 C、 D、6. 如图,已知 内接于 是 的直径, 与 相切,切点为 ,若 ,则 ( )度. A、 B、 C、 D、7. 抛物线y=(x﹣2)2﹣1可以由抛物线y=x2平移而得到,下列平移正确的是( )
A、 B、 C、 D、7. 抛物线y=(x﹣2)2﹣1可以由抛物线y=x2平移而得到,下列平移正确的是( )
A、先向左平移2个单位长度,然后向上平移1个单位长度 B、先向左平移2个单位长度,然后向下平移1个单位长度 C、先向右平移2个单位长度,然后向上平移1个单位长度 D、先向右平移2个单位长度,然后向下平移1个单位长度8. 如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A,B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为( )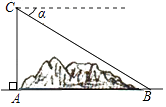 A、800sinα米 B、800tanα米 C、 米 D、 米9. 如图,将二次函数 的图像沿 轴对折,得到的新的二次函数的表达式是( )
A、800sinα米 B、800tanα米 C、 米 D、 米9. 如图,将二次函数 的图像沿 轴对折,得到的新的二次函数的表达式是( ) A、 B、 C、 D、10. 已知抛物线 的图象如图所示,下列说法正确的是( )
A、 B、 C、 D、10. 已知抛物线 的图象如图所示,下列说法正确的是( ) A、 B、 C、当 时, 的最大值为 D、 的解是11. 如图,正方形 中,分别以 为圆心,以正方形的边长 为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为( )
A、 B、 C、当 时, 的最大值为 D、 的解是11. 如图,正方形 中,分别以 为圆心,以正方形的边长 为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为( ) A、 B、 C、 D、12. 抛物线 上部分点的横坐标 ,纵坐标 的对应值如下表:
A、 B、 C、 D、12. 抛物线 上部分点的横坐标 ,纵坐标 的对应值如下表:…
-2
-1
0
1
2
…
…
0
4
6
6
4
…
从上表可知,下列说法:
①抛物线与 轴的一个交点为 ;②函数 的最大值为 ;③抛物线的对称轴是 ④在对称轴左侧, 随 增大而增大.其中正确的是( )
A、①②③ B、①③④ C、①②④ D、②③④二、填空题
-
13. 在“阳光体育”活动期间,班主任将全班同学随机分成了4组进行活动,该班小明和小亮同学被分在同一组的概率是.14. 如图,一直线经过原点 且与反比例函数 相交于点 ,点 过点 作 轴,垂足为 ,连接 .则 面积为 .
 15. 如图,半圆 的直径 弦 平分 ,则弧 的长为 (结果用π表示)
15. 如图,半圆 的直径 弦 平分 ,则弧 的长为 (结果用π表示) 16. 若方程 的两个根是 和 ,那么二次函数 的图象的对称轴是直线17. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至 处时,测得岛屿 恰好在其正北方向,继续向东航行1小时到达 处,测得岛屿 在其北偏西 方向,保持航向不变又航行2小时到达 处,此时海监船与岛的 之间的距离(即 的长)为海里. (结果用根号表示)
16. 若方程 的两个根是 和 ,那么二次函数 的图象的对称轴是直线17. 如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至 处时,测得岛屿 恰好在其正北方向,继续向东航行1小时到达 处,测得岛屿 在其北偏西 方向,保持航向不变又航行2小时到达 处,此时海监船与岛的 之间的距离(即 的长)为海里. (结果用根号表示) 18. 如图,将半径为 的圆形纸片沿 折叠后,圆弧恰好能经过圆心 用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为 .(结果用含根号的式子表示)
18. 如图,将半径为 的圆形纸片沿 折叠后,圆弧恰好能经过圆心 用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为 .(结果用含根号的式子表示)
三、解答题
-
19. 一个不透明的布袋里装有6个白球,2个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为 .(1)、布袋里红球的个数;(2)、小亮和小丽将布袋中的白球取出5个,利用剩下的球进行摸球游戏,他们约定:先摸出 个球后不放回,再摸出1个球,若两个球中有红球则小亮胜,否则小丽胜,你认为这个游戏公平吗?请用列表或画树状图说明理由.20. 目前,某市正在积极创建全国文明城市,交通部门一再提醒司机:为了安全,请勿超速,并进一步完善各类监测系统,如图,在公路某直线路段 内限速60千米/小时,为了检测车辆是否超速,在公路 旁设立了观测点 从观测点 测得一小车从点 到达点 行驶了5秒钟,已知 米,此车超速了吗?请说明理由,(参考数据: )
 21. 如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
21. 如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D. (1)、求这两个函数的解析式:(2)、求△ADC的面积.22. 已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点,
(1)、求这两个函数的解析式:(2)、求△ADC的面积.22. 已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点, (1)、求这个二次函数的解析式(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6.求点B的坐标。23. 如图,已知点 在反比例函数 的图象上,点 在直线 的图象上,点 的纵坐标为 , 轴,且
(1)、求这个二次函数的解析式(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6.求点B的坐标。23. 如图,已知点 在反比例函数 的图象上,点 在直线 的图象上,点 的纵坐标为 , 轴,且 (1)、求 的值;(2)、点 在 轴上, 是等腰三角形,求点 的坐标.24. 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E。
(1)、求 的值;(2)、点 在 轴上, 是等腰三角形,求点 的坐标.24. 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E。 (1)、求证:直线EF是⊙O的切线。
(1)、求证:直线EF是⊙O的切线。
(2)、求cos∠E的值。
25. 如图,已知一次函数 的图象与 轴交于点 ,与二次函数 的图象交于 轴上的一点 二次函数 的图象与 轴只有唯一的交点 ,且 .
 (1)、求二次函数的表达式;(2)、点 为一次函数下方抛物线上的点, 的面积最大时,求点 的坐标;(3)、设一次函数 的图象与二次函数的图象的另一交点为 ,已知 为 轴上的一个动点,且 为直角三角形,求点 的坐标.
(1)、求二次函数的表达式;(2)、点 为一次函数下方抛物线上的点, 的面积最大时,求点 的坐标;(3)、设一次函数 的图象与二次函数的图象的另一交点为 ,已知 为 轴上的一个动点,且 为直角三角形,求点 的坐标.