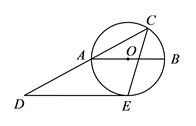山东省日照市岚山区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 垃圾分类是一种文明健康的生活方式.下列垃圾分类标识分别代表可回收物、厨余垃圾、有害垃圾和其它垃圾.其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图所示的几何体的俯视图是( )
2. 如图所示的几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 下列事件为必然事件的是( )A、任意画一个三角形,其内角和是180° B、打开电视机,正在播放新闻 C、经过有交通信号灯的路口,遇到绿灯 D、掷一枚质地均匀的硬币,正面朝上4. 如图,在 中,∠C=90°,设∠A , ∠B , ∠C所对的边分别为a , b , c , 则( )
3. 下列事件为必然事件的是( )A、任意画一个三角形,其内角和是180° B、打开电视机,正在播放新闻 C、经过有交通信号灯的路口,遇到绿灯 D、掷一枚质地均匀的硬币,正面朝上4. 如图,在 中,∠C=90°,设∠A , ∠B , ∠C所对的边分别为a , b , c , 则( ) A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB5. 用配方法解一元二次方程 ,配方正确的是( )A、 B、 C、 D、6. 如图,线段AB的两个端点坐标分别是A(2,6),B(6,4),以原点O为位似中心,在第一象限内将线段AB为原来的 后得到线段CD,端点C的坐标是( )
A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB5. 用配方法解一元二次方程 ,配方正确的是( )A、 B、 C、 D、6. 如图,线段AB的两个端点坐标分别是A(2,6),B(6,4),以原点O为位似中心,在第一象限内将线段AB为原来的 后得到线段CD,端点C的坐标是( ) A、(1,3) B、(3,2) C、( ,2) D、(2, )7. 如图,AB是⊙O的直径,AB=10,弦CD⊥AB于点E,若OA:OE=5:3,则弦CD的长为( )
A、(1,3) B、(3,2) C、( ,2) D、(2, )7. 如图,AB是⊙O的直径,AB=10,弦CD⊥AB于点E,若OA:OE=5:3,则弦CD的长为( ) A、3 B、4 C、6 D、88. 如图,一张长为a宽为b的矩形纸片(a>b),将纸片沿较长边的中点对折,得到的两个小矩形都和原来的矩形相似,则a:b的值是( )
A、3 B、4 C、6 D、88. 如图,一张长为a宽为b的矩形纸片(a>b),将纸片沿较长边的中点对折,得到的两个小矩形都和原来的矩形相似,则a:b的值是( ) A、 B、 C、 D、9. 在同一平面直角坐标系中,反比例函数y (b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是( )A、
A、 B、 C、 D、9. 在同一平面直角坐标系中,反比例函数y (b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是( )A、 B、
B、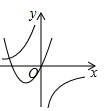 C、
C、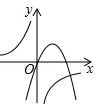 D、
D、 10. 如图,圆内接正方形的边长为2,以其各边为直径作半圆,则图中阴影部分的面积为( )
10. 如图,圆内接正方形的边长为2,以其各边为直径作半圆,则图中阴影部分的面积为( ) A、4 B、 C、 D、11. 若关于x的一元二次方程 有实数根,则整数a的最大值为( )A、−2 B、−1 C、1 D、212. 已知二次函数 的图象如图所示,顶点坐标为(m,3),则下列结论:① ;② ;③ ;④关于x的一元二次方程 有两个相等的实数根.其中正确结论的个数是( )
A、4 B、 C、 D、11. 若关于x的一元二次方程 有实数根,则整数a的最大值为( )A、−2 B、−1 C、1 D、212. 已知二次函数 的图象如图所示,顶点坐标为(m,3),则下列结论:① ;② ;③ ;④关于x的一元二次方程 有两个相等的实数根.其中正确结论的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 计算 = .14. 若一元二次方程 的两根为x1 , x2 , 则x1(1−x2)+x2的值是 .15. 如图,D、E分别在△ABC的边AC、AB上,若△ADE∽△ABC,AD=2,AE=3,BE=7,则AC的长为 .
 16. 如图,点A1、A2、A3、A4…分别在x轴正半轴上,△A1OB1、△A1 A2B2、△A2 A3B3、△A3 A4B4…分别是以A1、A2、A3、A4…为直角顶点的等腰直角三角形,其斜边的中点C1(x1 , y1)、C2(x2 , y2)、C3(x3 , y3)、C4(x4 , y4)…均在反比例函数 的图象上,则y1+ y2+ y3+ y4+…+ y10= .
16. 如图,点A1、A2、A3、A4…分别在x轴正半轴上,△A1OB1、△A1 A2B2、△A2 A3B3、△A3 A4B4…分别是以A1、A2、A3、A4…为直角顶点的等腰直角三角形,其斜边的中点C1(x1 , y1)、C2(x2 , y2)、C3(x3 , y3)、C4(x4 , y4)…均在反比例函数 的图象上,则y1+ y2+ y3+ y4+…+ y10= .
三、解答题
-
17. 如图,在每个小正方形边长都是1的方格纸中,点O、A、B都在格点上.
 (1)、画出△AOB绕点O顺时针旋转90°后的△A1OB1;(2)、求点B旋转到点B1时所经过的路径长.18. 如图是某游乐园“水上滑梯”的侧面示意图,其中BD段可看成双曲线 的一部分,矩形OABC是向上攀爬的阶梯部分.以O为中心建立平面直角坐标系,使点A和点C分别落在x轴和y轴的正半轴上.已知OC=5米,入口平台BC=1.8米,滑梯的出口D点到水面的距离DE为0.75米(O、A、E在一条直线上).求B、D之间的水平距离AE的长.
(1)、画出△AOB绕点O顺时针旋转90°后的△A1OB1;(2)、求点B旋转到点B1时所经过的路径长.18. 如图是某游乐园“水上滑梯”的侧面示意图,其中BD段可看成双曲线 的一部分,矩形OABC是向上攀爬的阶梯部分.以O为中心建立平面直角坐标系,使点A和点C分别落在x轴和y轴的正半轴上.已知OC=5米,入口平台BC=1.8米,滑梯的出口D点到水面的距离DE为0.75米(O、A、E在一条直线上).求B、D之间的水平距离AE的长. 19. 一个不透明的口袋里装有红、黄、白三种颜色的乒乓球(除颜色外其余都相同),其中红球和黄球各1个,白球2个.(1)、小惠从口袋中随机摸出一个球,这个球是白球的概率是;(2)、小惠先从口袋中随机摸出一个球,记录下颜色后不放回,再从袋子里剩余的球中随机摸出一个球,记录下球的颜色.请你用列表法或画树状图法求出小惠两次摸出的球中有一个是白球的概率.20. 为进一步完善全民健身公共服务体系,满足人民群众体育健身需求,我市将学校体育场地设施向社会开放作为重要民生项目.某学校利用节假日和早晚非教学时间将田径场,足球场地对外开放.据统计,第一个周场地对外接纳64人次,场地对外接纳人次逐周增加,第三个周场地对外接纳144人次,若场地对外接纳人次的周平均增长率相同.(1)、求场地对外接纳人次的周平均增长率;(2)、因条件限制,该学校体育场地每周接纳能力不超过220人次,在场地对外接纳人次周平均增长率不变的条件下,学校体育场地能否接纳第四周的校外进场人次?并说明理由.
19. 一个不透明的口袋里装有红、黄、白三种颜色的乒乓球(除颜色外其余都相同),其中红球和黄球各1个,白球2个.(1)、小惠从口袋中随机摸出一个球,这个球是白球的概率是;(2)、小惠先从口袋中随机摸出一个球,记录下颜色后不放回,再从袋子里剩余的球中随机摸出一个球,记录下球的颜色.请你用列表法或画树状图法求出小惠两次摸出的球中有一个是白球的概率.20. 为进一步完善全民健身公共服务体系,满足人民群众体育健身需求,我市将学校体育场地设施向社会开放作为重要民生项目.某学校利用节假日和早晚非教学时间将田径场,足球场地对外开放.据统计,第一个周场地对外接纳64人次,场地对外接纳人次逐周增加,第三个周场地对外接纳144人次,若场地对外接纳人次的周平均增长率相同.(1)、求场地对外接纳人次的周平均增长率;(2)、因条件限制,该学校体育场地每周接纳能力不超过220人次,在场地对外接纳人次周平均增长率不变的条件下,学校体育场地能否接纳第四周的校外进场人次?并说明理由.