山东省青岛市市南区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 如图的一个几何体,其左视图是( )
 A、
A、 B、
B、 C、
C、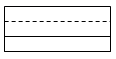 D、
D、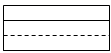 2. 一个不透明的口袋中装有10个黑球和若干个白球,小球除颜色外其余均相同,从中随机摸出一球记下颜色,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,由此估计口袋中白球的个数约为( )A、10个 B、20个 C、30个 D、40个3. 已知关于x的方程x2+2x+k=0有实数根,则k的值为( )A、k≤1 B、k<1 C、k≥1 D、k>14. 反比例函数y 的图象上有三个点,分别是(x1 , y1)(x2 , y2)(x3 , y3),若x1<0<x2<x3 , 则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y2<y3<y15. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),则下列结论中正确的是( )
2. 一个不透明的口袋中装有10个黑球和若干个白球,小球除颜色外其余均相同,从中随机摸出一球记下颜色,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,由此估计口袋中白球的个数约为( )A、10个 B、20个 C、30个 D、40个3. 已知关于x的方程x2+2x+k=0有实数根,则k的值为( )A、k≤1 B、k<1 C、k≥1 D、k>14. 反比例函数y 的图象上有三个点,分别是(x1 , y1)(x2 , y2)(x3 , y3),若x1<0<x2<x3 , 则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y2<y3<y15. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),则下列结论中正确的是( ) A、AB2=AP2+BP2 B、BP2=AP•BA C、 D、6. 将函数y=(x+1)2﹣4的图象先向右平移2个单位长度,再向上平移4个单位长度,则得到的函数解析式为( )A、y=(x﹣1)2 B、y=(x﹣1)2﹣8 C、y=(x+3)2 D、y=(x+3)2﹣87. 如图,在菱形ABCD中,E是AD边的中点,连接BE交AC于点F,连接DF,下列四个结论:①△AEF∽△CBF,②CF=2AF,③DF=DC,④2S四边形CDEF=5S△ABF , 其中正确正确的结论有( )
A、AB2=AP2+BP2 B、BP2=AP•BA C、 D、6. 将函数y=(x+1)2﹣4的图象先向右平移2个单位长度,再向上平移4个单位长度,则得到的函数解析式为( )A、y=(x﹣1)2 B、y=(x﹣1)2﹣8 C、y=(x+3)2 D、y=(x+3)2﹣87. 如图,在菱形ABCD中,E是AD边的中点,连接BE交AC于点F,连接DF,下列四个结论:①△AEF∽△CBF,②CF=2AF,③DF=DC,④2S四边形CDEF=5S△ABF , 其中正确正确的结论有( ) A、4个 B、3个 C、2个 D、1个8. 在同一平面直角坐标系中,二次函数y=ax2+bx,一次函数y=ax+b和反比例函数y 的图象可能是( )A、
A、4个 B、3个 C、2个 D、1个8. 在同一平面直角坐标系中,二次函数y=ax2+bx,一次函数y=ax+b和反比例函数y 的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 若 ,则 的值为 .10. 随着国家“惠民政策”的陆续出台,为了切实让老百姓得到实惠,某种药品原价198元/瓶,经过连续两次降价后,现仅售78元/瓶,假定两次降价的百分率相同,设该种药品平均每次降价的百分率为x,则列出的关于x方程为 .11. 如图,在平面直角坐标系中,△ABC的三个顶点分别在格点上,其中A(3,2)、B(1,﹣1)、C(4,0).以点B为位似中心,在y轴的右侧,将△ABC放大为原来的2倍,得到△A1B1C1则点A的对应点A1的坐标为 .
 12. 在△ABC中,AB=5,BC=8,AD是BC边上的高,AD=4,则tanC= .13. 已知线段a的长度为11,现从1~10这10条整数线段中任取两条,能和线段a组成三角形的概率为 .14. 如图,在矩形ABCD中,AB=4,∠ACB=30°,E,F分别为对角线AC与边CD上的点,且AE=CF,则BE+BF的最小值为 .
12. 在△ABC中,AB=5,BC=8,AD是BC边上的高,AD=4,则tanC= .13. 已知线段a的长度为11,现从1~10这10条整数线段中任取两条,能和线段a组成三角形的概率为 .14. 如图,在矩形ABCD中,AB=4,∠ACB=30°,E,F分别为对角线AC与边CD上的点,且AE=CF,则BE+BF的最小值为 .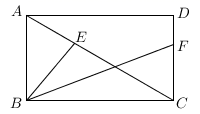
三、解答题
-
15. 已知:∠A和∠A一边上的点B.求作:▱ABCD,满足∠A是它的一个内角,且对角线BD⊥AD.
 16.(1)、解方程:2x2+4x﹣3=0;(2)、计算:sin245°+tan60°•cos30°.17. 为落实“十个一“活动,学校组建了多个志愿者服务队,小盖和小吕通过做游戏决定谁优先选择服务队,游戏规则:两人各掷一次质地均匀的骰子,如果掷出的点数之和是小于7的偶数,由小盖优先选择服务队;如果掷出的点数之和是大于6的奇数,由小吕优先选择服务队.请你利用画树状图或列表的方法,判断这个游戏对双方是否公平.18. 小颖的数学学习日记:x月x日:测量旗杆的高度.
16.(1)、解方程:2x2+4x﹣3=0;(2)、计算:sin245°+tan60°•cos30°.17. 为落实“十个一“活动,学校组建了多个志愿者服务队,小盖和小吕通过做游戏决定谁优先选择服务队,游戏规则:两人各掷一次质地均匀的骰子,如果掷出的点数之和是小于7的偶数,由小盖优先选择服务队;如果掷出的点数之和是大于6的奇数,由小吕优先选择服务队.请你利用画树状图或列表的方法,判断这个游戏对双方是否公平.18. 小颖的数学学习日记:x月x日:测量旗杆的高度. (1)、今天上午王老师要带我们去操场测量旗杆的高度,昨天我们小组设计了一个方案,方案如下:小亮拿着标杆垂直于地面放置,我和小聪用卷尺测量标杆、标杆的影长和旗杆的影长,如图1所示,标杆AB=a,影长BC=b,旗杆的影长DF=c,则可求得旗杆DE的高度为 .(2)、但今天测量时,阴天没有阳光,就不能用以上的方案了.如图2所示,王老师将升旗用的绳子拉直,使绳子的底端G刚好触到地面,用仪器测得绳子与地面的夹角为37°,然后又将绳子拉到一个0.5米高的平台上,拉直绳子使绳子上的H点刚好触到平台,剩余的绳子长度为5米,此时测得绳子与平台的夹角为54°,利用这些数据能求出旗杆DE的高度吗?(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75;sin54°≈0.8,cos54°≈0.58,tan54°≈1.45)请你回答小颖的问题.若能,请求出旗杆的高度;若不能,请说明理由.19. 在“学习一项体育技能”活动中,小明作为学生代表去观看“青岛黄海足球队”的训练.他看到队员们在做掷界外球训练,甲球员要将足球掷给离他7.5米远的乙球员,掷出足球的运行轨还是一条抛物线,足球行进的高度y(米)与水平距离x(米)之间的关系如图所示,足球出手时离地面的高度为2米,在距离甲球员4米处达到最大高度3.6米.若不计其他因素,身高1.85米的乙球员要能触到足球,他垂直起跳的高度至少要达到多少米?
(1)、今天上午王老师要带我们去操场测量旗杆的高度,昨天我们小组设计了一个方案,方案如下:小亮拿着标杆垂直于地面放置,我和小聪用卷尺测量标杆、标杆的影长和旗杆的影长,如图1所示,标杆AB=a,影长BC=b,旗杆的影长DF=c,则可求得旗杆DE的高度为 .(2)、但今天测量时,阴天没有阳光,就不能用以上的方案了.如图2所示,王老师将升旗用的绳子拉直,使绳子的底端G刚好触到地面,用仪器测得绳子与地面的夹角为37°,然后又将绳子拉到一个0.5米高的平台上,拉直绳子使绳子上的H点刚好触到平台,剩余的绳子长度为5米,此时测得绳子与平台的夹角为54°,利用这些数据能求出旗杆DE的高度吗?(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75;sin54°≈0.8,cos54°≈0.58,tan54°≈1.45)请你回答小颖的问题.若能,请求出旗杆的高度;若不能,请说明理由.19. 在“学习一项体育技能”活动中,小明作为学生代表去观看“青岛黄海足球队”的训练.他看到队员们在做掷界外球训练,甲球员要将足球掷给离他7.5米远的乙球员,掷出足球的运行轨还是一条抛物线,足球行进的高度y(米)与水平距离x(米)之间的关系如图所示,足球出手时离地面的高度为2米,在距离甲球员4米处达到最大高度3.6米.若不计其他因素,身高1.85米的乙球员要能触到足球,他垂直起跳的高度至少要达到多少米? 20. 如图,直线y=kx+3与x轴、y轴分别交于点B、C,与反比例函数y 交于点A、D,过D做DE⊥x轴于E,连接OA,OD,若A(﹣2,n),S△OAB:S△ODE=1:2.
20. 如图,直线y=kx+3与x轴、y轴分别交于点B、C,与反比例函数y 交于点A、D,过D做DE⊥x轴于E,连接OA,OD,若A(﹣2,n),S△OAB:S△ODE=1:2. (1)、求反比例函数的表达式;(2)、求点C的坐标.21. 已知:如图,在平行四边形ABCD中,E、F分别为AB、CD的中点,G、H分别为DE、BF的中点.
(1)、求反比例函数的表达式;(2)、求点C的坐标.21. 已知:如图,在平行四边形ABCD中,E、F分别为AB、CD的中点,G、H分别为DE、BF的中点. (1)、试判断四边形EHFG的形状,并证明;(2)、若∠ABC=90°,试判断四边形EHFG的形状并加以并证明.22. 某快餐店新推出一种外卖,每份的成本为20元,推出后每份售价为50元,每月可售出200份,经过试卖发现,该外卖每份售价每降价1元,每月可多卖出10份,由于制作能力有限,每月最多制作该外卖350份.设该外卖每份售价x元(x≤50),每月的销售利润为w元.(1)、求w与x之间的函数关系式;(2)、该外卖每份售价多少元时,每月的销售利润最大?最大利润是多少?(3)、该外卖每份售价在什么范围时,每月的销售利润不低于4000元.23. 问题提出:如图1,D、E分别在△ABC的边AB、AC上,连接DE,已知线段AD=a,DB=b,AE=c,EC=d,则S△ADE , S△ABC和a,b,c,d之间会有怎样的数量关系呢?
(1)、试判断四边形EHFG的形状,并证明;(2)、若∠ABC=90°,试判断四边形EHFG的形状并加以并证明.22. 某快餐店新推出一种外卖,每份的成本为20元,推出后每份售价为50元,每月可售出200份,经过试卖发现,该外卖每份售价每降价1元,每月可多卖出10份,由于制作能力有限,每月最多制作该外卖350份.设该外卖每份售价x元(x≤50),每月的销售利润为w元.(1)、求w与x之间的函数关系式;(2)、该外卖每份售价多少元时,每月的销售利润最大?最大利润是多少?(3)、该外卖每份售价在什么范围时,每月的销售利润不低于4000元.23. 问题提出:如图1,D、E分别在△ABC的边AB、AC上,连接DE,已知线段AD=a,DB=b,AE=c,EC=d,则S△ADE , S△ABC和a,b,c,d之间会有怎样的数量关系呢? (1)、问题解决:探究一:
(1)、问题解决:探究一:①看到这个问题后,我们可以考虑先从特例入手,找出其中的规律.如图2,若DE∥BC,则∠ADE=∠B,且∠A=∠A,所以△ADE∽△ABC,可得比例式: 而根据相似三角形面积之比等于相似比的平方.可得 .根据上述这两个式子,可以推出: .
②如图3,若∠ADE=∠C,上述结论还成立吗?若成立,请写出证明过程;着不成立,请说明理由.
(2)、探究二:回到最初的问题,若图1中没有相似的条件,是否仍存在结论: ?方法回顾:两个三角形面积之比,不仅可以在相似的条件下求得,当两个三角形的底成高具有一定的关系时,也可以解决.如图4,D在△ABC的边上,做AH⊥BC于H,可得: .借用这个结论,请你解决最初的问题.延伸探究:
①如图5,D、E分别在△ABC的边AB、AC反向延长线上,连接DE,已知线段AD=a,AB=b,AE=c,AC=d,则 .
②如图6,E在△ABC的边AC上,D在AB反向延长线上,连接DE,已知线段AD=a,AB=b,AE=c,AC=d, .
(3)、结论应用:如图7,在平行四边形ABCD中,G是BC边上的中点,延长GA到E,连接DE交BA的延长线于F,若AB=5,AG=4,AE=2,▱ABCD的面积为30,则△AEF的面积是 .24. 已知:如图,在△ABC中,AB=AC=5cm,BC=8cm,AD⊥BC,垂足为D,F为AD中点.点P从点B出发,沿BC向点C匀速运动,速度为1cm/s同时,点Q从点A出发,沿AB向点B匀速运动,速度为1cm/s;点E为点P关于AD的对称点.连接PQ、FQ、EF、AE.设运动时间为t(s)(0<t<4),解答下列问题: (1)、当PQ∥AE时,求t的值;(2)、设四边形AEPQ的面积为y(cm2),试确定y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使∠DFE=∠AFQ?若存在,求出t的值;若不存在,请说明理由.
(1)、当PQ∥AE时,求t的值;(2)、设四边形AEPQ的面积为y(cm2),试确定y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使∠DFE=∠AFQ?若存在,求出t的值;若不存在,请说明理由.