山东省青岛市市北区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
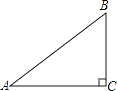
1. 如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值是( )
 A、 B、 C、 D、2. 下列结论中正确的是( )
A、 B、 C、 D、2. 下列结论中正确的是( )①在阳光照射下,同一时刻的物体,影子的方向是相同的.②物体在任何光线照射下影子的方向都是相同的.③固定的物体在路灯照射下,影子的方向与路灯的位置有关.④固定的物体在光线照射下,影子的长短仅与物体的长短有关.
A、①③ B、①③④ C、①④ D、②④3. 在一个不透明的口袋中,装有除颜色外其他都相同的4个白球和 个黄球,某同学进行如下试验:从袋中随机摸出1个球记下它的颜色,放回、摇匀,为一次摸球试验.记录摸球的次数与摸出白球的次数的列表如下:摸球试验的次数
100
200
500
1000
摸出白球的次数
21
39
102
199
根据列表可以估计出n的值为( )
A、4 B、16 C、20 D、244. 如图所示,大鱼与小鱼是位似图形,则小鱼上的点 对应大鱼上的点( )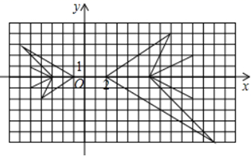 A、 B、 C、 D、5. 在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺品长 ,宽 .中间镶有宽度相同的三条丝绸花边.若丝绸花边的面积为 ,设丝绸花边的宽为 ,根据题意,可列方程为( )
A、 B、 C、 D、5. 在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺品长 ,宽 .中间镶有宽度相同的三条丝绸花边.若丝绸花边的面积为 ,设丝绸花边的宽为 ,根据题意,可列方程为( )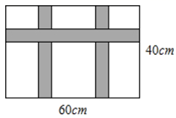 A、 B、 C、 D、6. 将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是( )
A、 B、 C、 D、6. 将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是( )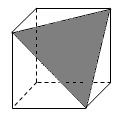 A、
A、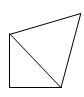 B、
B、 C、
C、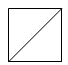 D、
D、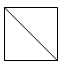 7. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、8. 如图,线段 ,点 是线段 的黄金分割点(且 ),点 是线段 的黄金分割点( ),点 是线段 的黄金分割点 依此类推,则线段 的长度是( )
7. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、8. 如图,线段 ,点 是线段 的黄金分割点(且 ),点 是线段 的黄金分割点( ),点 是线段 的黄金分割点 依此类推,则线段 的长度是( )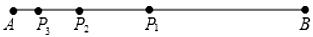 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
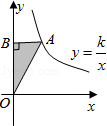
9. 若 ,则 .10. 如图,已知A点是反比例函数 (k≠0)的图象上一点,AB⊥y轴于B,且 ABO的面积为3,则k的值为 .
 11. 某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作,去年已投入5亿元资金,并计划投入资金逐年增长,明年将投入7.2亿元资金用于保障性住房建设,则这两年投入资金的年平均增长率为.12. 如图,边长分别为 和 的两个正方形 和 并排放在一起,连结 并延长交 于点 ,交 于点 .则线段 的长是 .
11. 某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作,去年已投入5亿元资金,并计划投入资金逐年增长,明年将投入7.2亿元资金用于保障性住房建设,则这两年投入资金的年平均增长率为.12. 如图,边长分别为 和 的两个正方形 和 并排放在一起,连结 并延长交 于点 ,交 于点 .则线段 的长是 .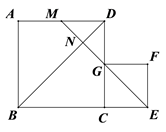 13. 如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度 ,则AC的长度是cm.
13. 如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度 ,则AC的长度是cm.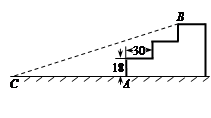 14. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号)
14. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号)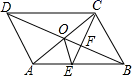
三、解答题
-
15. 已知:线段 如图所示.
求作:正方形 ,使得 .
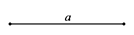 16.(1)、解方程: ;(2)、若抛物线 与 轴有交点,求 的取值范围.17. 在一个不透明的盒子中只装2枚白色棋子和2枚黑色棋子,它们除颜色外其余均相同.从这个盒子中随机地摸出 枚棋子,记下颜色后放回,搅匀后再随机地摸出 枚棋子记下颜色.(1)、请用画树状图(或列表)的方法,求两次摸出的棋子是不同颜色的概率.(2)、若小明、小亮做游戏,游戏规则是:两次摸出的棋子颜色不同则小明获胜,否则小亮获胜.你认为这个游戏公平吗?请说明理由.18. 水果店的张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.若销售这种水果想要每天盈利300元,求张阿姨需将每斤的售价定为多少元.19. 如图,一艘货轮由 港沿北偏东60度方向航行100海里到达 港,装配好货物再沿北偏西58度方向航行运抵 港, 港在 港的正北方向.求 两港之间的距离.(结果精确到 海里)
16.(1)、解方程: ;(2)、若抛物线 与 轴有交点,求 的取值范围.17. 在一个不透明的盒子中只装2枚白色棋子和2枚黑色棋子,它们除颜色外其余均相同.从这个盒子中随机地摸出 枚棋子,记下颜色后放回,搅匀后再随机地摸出 枚棋子记下颜色.(1)、请用画树状图(或列表)的方法,求两次摸出的棋子是不同颜色的概率.(2)、若小明、小亮做游戏,游戏规则是:两次摸出的棋子颜色不同则小明获胜,否则小亮获胜.你认为这个游戏公平吗?请说明理由.18. 水果店的张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.若销售这种水果想要每天盈利300元,求张阿姨需将每斤的售价定为多少元.19. 如图,一艘货轮由 港沿北偏东60度方向航行100海里到达 港,装配好货物再沿北偏西58度方向航行运抵 港, 港在 港的正北方向.求 两港之间的距离.(结果精确到 海里)(参考数据: )
 20. 已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF
20. 已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF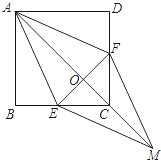 (1)、求证:BE = DF;(2)、连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.21. 在一次篮球比赛中,如图,队员甲正在投篮.已知球出手时离地面 ,与篮圈中心的水平距离为 ,球出手后水平距离为 时达到最大高度 ,设篮球运行轨迹为抛物线,篮圈距地面 .
(1)、求证:BE = DF;(2)、连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.21. 在一次篮球比赛中,如图,队员甲正在投篮.已知球出手时离地面 ,与篮圈中心的水平距离为 ,球出手后水平距离为 时达到最大高度 ,设篮球运行轨迹为抛物线,篮圈距地面 .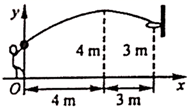 (1)、建立如图所示的平面直角坐标系,求此抛物线的解析式;(2)、此时球能否准确投中?(3)、此时,对方队员乙在甲面前 处跳起盖帽拦截,已知乙的最大摸高为 ,那么他能否获得成功?22. (问题提出)
(1)、建立如图所示的平面直角坐标系,求此抛物线的解析式;(2)、此时球能否准确投中?(3)、此时,对方队员乙在甲面前 处跳起盖帽拦截,已知乙的最大摸高为 ,那么他能否获得成功?22. (问题提出)小颖发现某座房屋的侧面是一种特殊的五边形,她决定好好研究一下它的特点,并计算它的面积.
(问题探究)
定义:如图(1),我们把满足 的五边形 叫做屋形.其中 叫做脊, 叫做腰, 叫做底.
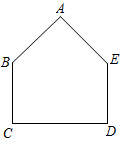
性质:
边:屋形的腰相等,脊相等;
角:①屋形腰与底的夹角相等;②脊与腰的夹角相等;
对角线:①
②屋形有两组对角线分别相等,且其中一组互相平分.
对称性:屋形是以底的垂直平分线为对称轴的轴对称图形;
(1)、请直接填写屋形对角线的性质①;(2)、请你根据定义证明“屋形的脊与腰的夹角相等”;已知:如图,五边形 是屋形.
求证:
证明:
(3)、(问题解决)
如图,在屋形 中,若 ,试求出屋形 的面积. 23. 已知:如图,在 中, ,垂足 ;点 从点 出发,沿 方向匀速运动,速度为 ,同时,点 从点 出发,沿 方向匀速运动,速度为 ;以 为底边作等腰三角形 ,使 ,并且 与 分别在 的两侧,连接 ,设运动时间为 .
23. 已知:如图,在 中, ,垂足 ;点 从点 出发,沿 方向匀速运动,速度为 ,同时,点 从点 出发,沿 方向匀速运动,速度为 ;以 为底边作等腰三角形 ,使 ,并且 与 分别在 的两侧,连接 ,设运动时间为 .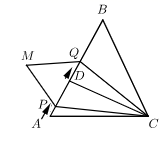
解答下列问题:
 (1)、当 时,是否存在某一时刻 ,使 ?若存在,求出此时 的值:若不存在,请说明理由;(2)、设四边形 的面积为 ,求当 时, 与 之间的函数关系式;(3)、是否存在某一时刻 ,使 与以 为顶点的三角形相似﹖若存在,请直接给出此时 的值;若不存在,请说明理由.
(1)、当 时,是否存在某一时刻 ,使 ?若存在,求出此时 的值:若不存在,请说明理由;(2)、设四边形 的面积为 ,求当 时, 与 之间的函数关系式;(3)、是否存在某一时刻 ,使 与以 为顶点的三角形相似﹖若存在,请直接给出此时 的值;若不存在,请说明理由.