山东省青岛市平度市2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. tan30°的值为( )A、 B、 C、 D、2. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
 B、
B、 C、
C、 D、
D、 3. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、154. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、5. 平度高铁通车后极大的方便了市民的出行.平度北站建设初期需要运送大量土石方.某运输公司承担了运送总量为106m3土石方的任务,该运输公司平均每天运送土石方的数量v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )A、 B、 C、 D、6. 一个三角形支架三条边长分别是75cm,100cm,120cm,现要再做一个与其相似的三角形木架,而只有长为60cm,120cm的两根木条,要求以其中一根为一边,从另一根上截下两段作为另两边(允许有余料),则不同的截法有( )A、一种 B、两种 C、三种 D、四种7. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
3. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、154. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、5. 平度高铁通车后极大的方便了市民的出行.平度北站建设初期需要运送大量土石方.某运输公司承担了运送总量为106m3土石方的任务,该运输公司平均每天运送土石方的数量v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )A、 B、 C、 D、6. 一个三角形支架三条边长分别是75cm,100cm,120cm,现要再做一个与其相似的三角形木架,而只有长为60cm,120cm的两根木条,要求以其中一根为一边,从另一根上截下两段作为另两边(允许有余料),则不同的截法有( )A、一种 B、两种 C、三种 D、四种7. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )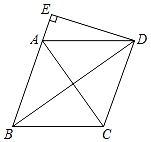 A、 B、 C、4 D、8. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、 B、 C、4 D、8. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )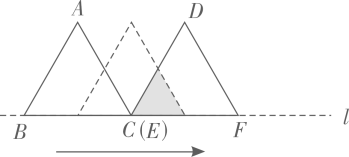 A、
A、 B、
B、 C、
C、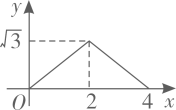 D、
D、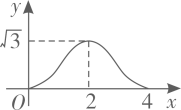
二、填空题
-
9. 在平面直角坐标系中,将 以点 为位似中心, 为位似比作位似变换,得到 .已知 ,则点 的坐标是 .
 10. 如图是一个几何体的三视图,该几何体的体积是 .
10. 如图是一个几何体的三视图,该几何体的体积是 .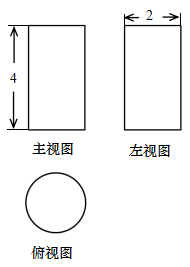 11. 如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上, .若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为 .
11. 如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上, .若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为 .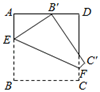 12. 如图,点A在反比例函数 的图象上,过点A作 轴,垂足为B,交反比例函数 的图象于点C.点P为y轴上一点,连接PA,PC,则 的面积为 .
12. 如图,点A在反比例函数 的图象上,过点A作 轴,垂足为B,交反比例函数 的图象于点C.点P为y轴上一点,连接PA,PC,则 的面积为 .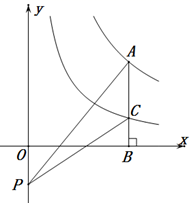 13. 如图是某剧场第一排座位分布图:甲、乙、丙、丁四人购票,所购票分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序 .
13. 如图是某剧场第一排座位分布图:甲、乙、丙、丁四人购票,所购票分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序 .
三、解答题
-
14. 如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA ,则BD的长度为 .
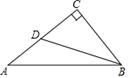 15. 已知:线段a和线段b.
15. 已知:线段a和线段b.求作:菱形ABCD,使AB=a,AC=b.
 16.(1)、在平面直角坐标系xOy中,二次函数图象的顶点坐标为(4,-3),该图象与x轴相交于点A,若点A的横坐标为1.求该二次函数的表达式.(2)、若抛物线 经过点A(2,m)和点B(3,n),试比较m和n的大小,并说明理由.17. 2022年冬奥会将在中国北京举行,小明和小刚都计划去观看冬奥项目比赛.他们都喜欢的冬奥项目分别是:A.“短道速滑”、B.“冰球”、C.“花样滑冰”和D.“跳台滑雪”.小明和小刚计划各自在这4个冬奥项目中任意选择一个观看,每个项目被选择的可能性相同.(1)、小明选择项目C.“花样滑冰”的概率是多少?(2)、用画树状图或列表的方法,求小明和小刚恰好选择同一项目观看的概率.18. 如图,一次函数y=mx+n(m≠0)的图象与反比例函数 (k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过A点作x轴的垂线,垂足为点C,已知△AOC的面积为4.
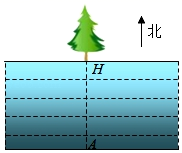
16.(1)、在平面直角坐标系xOy中,二次函数图象的顶点坐标为(4,-3),该图象与x轴相交于点A,若点A的横坐标为1.求该二次函数的表达式.(2)、若抛物线 经过点A(2,m)和点B(3,n),试比较m和n的大小,并说明理由.17. 2022年冬奥会将在中国北京举行,小明和小刚都计划去观看冬奥项目比赛.他们都喜欢的冬奥项目分别是:A.“短道速滑”、B.“冰球”、C.“花样滑冰”和D.“跳台滑雪”.小明和小刚计划各自在这4个冬奥项目中任意选择一个观看,每个项目被选择的可能性相同.(1)、小明选择项目C.“花样滑冰”的概率是多少?(2)、用画树状图或列表的方法,求小明和小刚恰好选择同一项目观看的概率.18. 如图,一次函数y=mx+n(m≠0)的图象与反比例函数 (k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过A点作x轴的垂线,垂足为点C,已知△AOC的面积为4.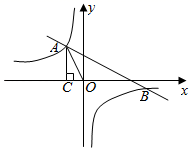 (1)、分别求出a和b的值.(2)、结合图象直接写出 中x的取值范围.19. 为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向.测量方案与数据如下表:
(1)、分别求出a和b的值.(2)、结合图象直接写出 中x的取值范围.19. 为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向.测量方案与数据如下表:课题
测量河流宽度
测量工具
测量角度的仪器,皮尺等
测量小组
第一小组
第二小组
第三小组
测量方案示意图
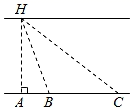
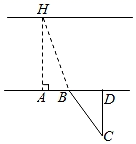
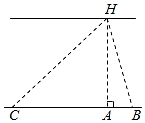
说明
点B,C在点A的正东方向
点B,D在点A的正东方向
点B在点A的正东方向,点C在点A的正西方向.
测量数据
BC=60m,
∠ABH=70°,
∠ACH=35°.
BD=20m,
∠ABH=70°,
∠BCD=35°.
BC=101m,
∠ABH=70°,
∠ACH=35°.
 (1)、哪个小组的数据无法计算出河宽?(2)、请选择其中一个方案及其数据求出河宽(精确到0.1m).(参考数据:sin70°≈0.94,sin35°≈0.57,tan70°≈2.75,tan35°≈0.70)20. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆 人次,进馆人次逐月增加,到第三个月末累计进馆 人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过 人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.21. 如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)、哪个小组的数据无法计算出河宽?(2)、请选择其中一个方案及其数据求出河宽(精确到0.1m).(参考数据:sin70°≈0.94,sin35°≈0.57,tan70°≈2.75,tan35°≈0.70)20. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆 人次,进馆人次逐月增加,到第三个月末累计进馆 人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过 人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.21. 如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.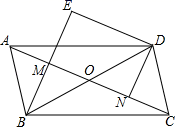 (1)、求证:△AMB≌△CND;(2)、若BD=2AB,判断四边形DEMN的形状,并证明你的结论.22. 某公司分别在A,B两城生产同种产品,共100件.A城生产产品的总成本y(万元)与产品数量x(件)之间具有函数关系y=ax2+bx.当x=10时,y=400;当x=20时,y=1000.B城生产产品的每件成本为70万元.(1)、求a,b的值;(2)、当A,B两城生产这批产品的总成本的和最少时,求A,B两城各生产多少件?23. 问题的提出:n个平面最多可以把空间分割成多少个部分?
(1)、求证:△AMB≌△CND;(2)、若BD=2AB,判断四边形DEMN的形状,并证明你的结论.22. 某公司分别在A,B两城生产同种产品,共100件.A城生产产品的总成本y(万元)与产品数量x(件)之间具有函数关系y=ax2+bx.当x=10时,y=400;当x=20时,y=1000.B城生产产品的每件成本为70万元.(1)、求a,b的值;(2)、当A,B两城生产这批产品的总成本的和最少时,求A,B两城各生产多少件?23. 问题的提出:n个平面最多可以把空间分割成多少个部分?问题的转化:由n上面问题比较复杂,所以我们先来研究跟它类似的一个较简单的问题:
n条直线最多可以把平面分割成多少个部分?
如图1,很明显,平面中画出1条直线时,会得到1+1=2个部分;所以,1条直线最多可以把平面分割成2个部分;
如图2,平面中画出第2条直线时,新增的一条直线与已知的1条直线最多有1个交点,这个交点会把新增的这条直线分成2部分,从而多出2个部分,即总共会得到1+1+2=4个部分,所以,2条直线最多可以把平面分割成4个部分;
如图3,平面中画出第3条直线时,新增的一条直线与已知的2条直线最多有2个交点,这2个交点会把新增的这条直线分成3部分,从而多出3个部分,即总共会得到1+1+2+3=7个部分,所以,3条直线最多可以把平面分割成7个部分;
平面中画出第4条直线时,新增的一条直线与已知的3条直线最多有3个交点,这3个交点会把新增的这条直线分成4部分,从而多出4个部分,即总共会得到1+1+2+3+4=11个部分,所以,4条直线最多可以把平面分割成11个部分;…

①请你仿照前面的推导过程,写出“5条直线最多可以把平面分割成多少个部分”的推导过程(只写推导过程,不画图);
②根据递推规律用n的代数式填空:n条直线最多可以把平面分割成几个部分.
问题的解决:借助前面的研究,我们继续开头的问题;n个平面最多可以把空间分割成多少个部分?
首先,很明显,空间中画出1个平面时,会得到1+1=2个部分;所以,1个平面最多可以把空间分割成2个部分;
空间中有2个平面时,新增的一个平面与已知的1个平面最多有1条交线,这1条交线会把新增的这个平面最多分成2部分,从而多出2个部分,即总共会得到1+1+2=4个部分,所以,2个平面最多可以把空间分割成4个部分;
空间中有3个平面时,新增的一个平面与已知的2个平面最多有2条交线,这2条交线会把新增的这个平面最多分成4部分,从而多出4个部分,即总共会得到1+1+2+4=8个部分,所以,3个平面最多可以把空间分割成8个部分;
空间中有4个平面时,新增的一个平面与已知的3个平面最多有3条交线,这3条交线会把新增的这个平面最多分成7部分,从而多出7个部分,即总共会得到1+1+2+4+7=15个部分,所以,4个平面最多可以把空间分割成15个部分;
空间中有5个平面时,新增的一个平面与已知的4个平面最多有4条交线,这4条交线会把新增的这个平面最多分成11部分,而从多出11个部分,即总共会得到1+1+2+4+7+11=26个部分,所以,5个平面最多可以把空间分割成26个部分;…
③请你仿照前面的推导过程,写出“6个平面最多可以把空间分割成多少个部分?”的推导过程(只写推导过程,不画图);
④根据递推规律填写结果:10个平面最多可以把空间分割成几个部分;
⑤设n个平面最多可以把空间分割成Sn个部分,设n-1个平面最多可以把空间分割成Sn−1个部分,前面的递推规律可以用Sn−1和n的代数式表示Sn;这个等式是Sn等于多少.
24. 如图,在四边形ABCD中,AB CD,∠D=90°,AC⊥BC,DC=8cm,AD=6cm.点F从A点出发,以2cm/s的速度沿AB向点B匀速运动,同时,点E从B点出发,以1 cm/s的速度沿BC向点C匀速运动.当其中一点到达终点时,两点都停止运动,设运动时间为t(s).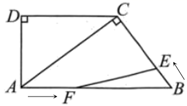 (1)、求AB长度;(2)、设四边形ACEF的面积为y (cm2),求y与t的函数关系式;(3)、是否存在某一时刻t,使得四边形ACEF的面积是△ACD的面积的 倍?若存在,求出此时t的值;若不存在,说明理由.(4)、求t为何值时△BEF为直角三角形.
(1)、求AB长度;(2)、设四边形ACEF的面积为y (cm2),求y与t的函数关系式;(3)、是否存在某一时刻t,使得四边形ACEF的面积是△ACD的面积的 倍?若存在,求出此时t的值;若不存在,说明理由.(4)、求t为何值时△BEF为直角三角形.