山东省青岛市即墨区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1.
如图所示的几何体的俯视图是( )
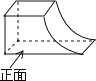 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,正方形ABCD中,对角线AC、BD交于点O,点M、N分别为OB、OC的中点,则sin∠OMN的值为( )
2. 如图,正方形ABCD中,对角线AC、BD交于点O,点M、N分别为OB、OC的中点,则sin∠OMN的值为( )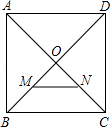 A、 B、1 C、 D、3. 在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
A、 B、1 C、 D、3. 在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:次数
1
2
3
4
5
6
7
8
9
10
黑棋数
1
3
0
2
3
4
2
1
1
3
根据以上数据,估算袋中的白棋子数量为( )
A、60枚 B、50枚 C、40枚 D、30枚4. 某商店今年10月份的销售额是2万元,12月份的销售额是2.88万元,从10月份到12月份,该商店销售额平均每月的增长率为( )A、44% B、22% C、20% D、10%5. 抛物线y=- 2x2 - 4x - 5经过平移后得到抛物线y=- 2x2 , 平移方法是( )A、向左平移1个单位,再向下平移3个单位 B、向左平移1个单位,再向上平移3个单位 C、向右平移1个单位,再向下平移3个单位 D、向右平移1个单位,再向上平移3个单位6. 若点A(x1 , ﹣6),B(x2 , ﹣2),C(x3 , 2)在反比例函数 的图象上,则x1 , x2 , x3的大小关系是( )A、x1<x2<x3 B、x2<x1<x3 C、x2<x3<x1 D、x3<x2<x17. 如图,在矩形ABCD中,AB=2,AD= ,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:①点B平分线段AF;②PF= DE;③∠BEF=∠FEC; ④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.其中正确结论的个数有( )个. A、2 B、3 C、4 D、58. 抛物线y=ax2+bx+c的图象如图所示,那么一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致是( )
A、2 B、3 C、4 D、58. 抛物线y=ax2+bx+c的图象如图所示,那么一次函数y=bx+b2﹣4ac与反比例函数y= 在同一坐标系内的图象大致是( )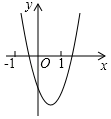 A、
A、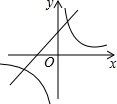 B、
B、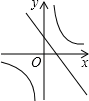 C、
C、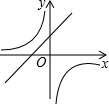 D、
D、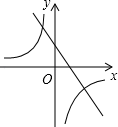
二、填空题
-
9. 一山坡的坡度 ,小刚从山坡脚下点 处上坡走了 米到达点 处,那么他上升的高度是米.10. 关于x的一元二次方程(a﹣1)x2﹣2x+3=0有实数根,则整数a的最大值是 .11. 一个几何体的三视图如图所示,则该几何体的表面积是 .
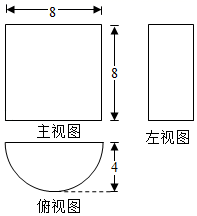 12. 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是 .
12. 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是 .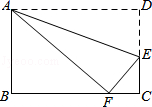 13. 如图,矩形ABCD的顶点A和对称中心均在反比例函数y= (k≠0,x>0)上,若矩形ABCD的面积为8,则k的值为 .
13. 如图,矩形ABCD的顶点A和对称中心均在反比例函数y= (k≠0,x>0)上,若矩形ABCD的面积为8,则k的值为 .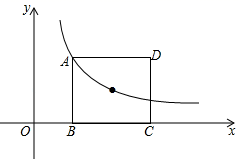 14. 如图,在矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点P,H,连接AH,若点P是CH的中点,则△APH的周长为
14. 如图,在矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点P,H,连接AH,若点P是CH的中点,则△APH的周长为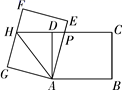
三、解答题
-
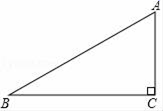
15. 如图,小刚爸爸要利用一块形状为直角三角形(∠C为直角)的铁皮加工一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上,请协助小刚爸爸用尺规画出裁割线.
 16.(1)、解方程:(x+1)(x﹣3)=2x﹣5;(2)、在体质检测时,初三某男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=﹣ x2+x+2,求铅球行进的最大高度是多少?17. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.18. 如图,在平面直角坐标系中,双曲线 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
16.(1)、解方程:(x+1)(x﹣3)=2x﹣5;(2)、在体质检测时,初三某男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=﹣ x2+x+2,求铅球行进的最大高度是多少?17. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.18. 如图,在平面直角坐标系中,双曲线 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.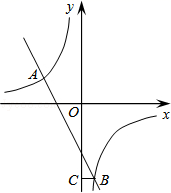 (1)、求双曲线和直线的解析式;(2)、直接写出不等式 的解集.19. 如图是一个横断面为抛物线形状的拱桥,当水面宽(AB)为4m时,拱顶(拱桥洞的最高点)离水面2m.当水面下降1m时,求水面的宽度增加了多少?
(1)、求双曲线和直线的解析式;(2)、直接写出不等式 的解集.19. 如图是一个横断面为抛物线形状的拱桥,当水面宽(AB)为4m时,拱顶(拱桥洞的最高点)离水面2m.当水面下降1m时,求水面的宽度增加了多少?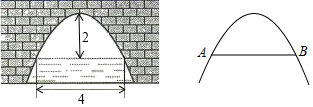 20. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高 所在的直线.为了测量房屋的高度,在地面上C点测得屋顶 的仰角为 ,此时地面上C点、屋檐上 点、屋顶上A点三点恰好共线,继续向房屋方向走 到达点D时,又测得屋檐 点的仰角为 ,房屋的顶层横梁 , , 交 于点G(点C,D, 在同一水平线上).(参考数据: , , , )
20. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高 所在的直线.为了测量房屋的高度,在地面上C点测得屋顶 的仰角为 ,此时地面上C点、屋檐上 点、屋顶上A点三点恰好共线,继续向房屋方向走 到达点D时,又测得屋檐 点的仰角为 ,房屋的顶层横梁 , , 交 于点G(点C,D, 在同一水平线上).(参考数据: , , , )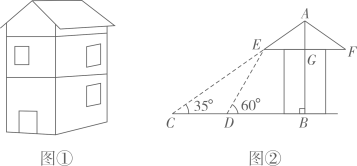 (1)、求屋顶到横梁的距离 ;(2)、求房屋的高 (结果精确到 ).21. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)、求屋顶到横梁的距离 ;(2)、求房屋的高 (结果精确到 ).21. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE. (1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)22. 我市某工艺厂设计了一款成本为10元 件的工艺品投放市场进行试销,经过调查,得到如下数据:
(1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)22. 我市某工艺厂设计了一款成本为10元 件的工艺品投放市场进行试销,经过调查,得到如下数据:销售单价 元 件
20
30
40
50
每天销售量 件
500
400
300
200
(1)、猜一猜y是x的什么函数关系?并求出此函数的关系式;(2)、若用 元 表示工艺厂试销该工艺品每天获得的利润,试求 元 与 元 件 之间的函数关系式.(3)、若该工艺品的每天的总成本不能超过2500元,那么销售单价定为多少元时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?23. 如图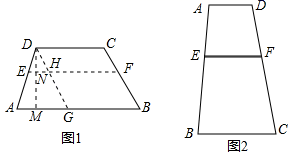
如图1,四边形ABCD中,AB∥CD,AB=a,CD=b(a≠b),点E、F分别是AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2 .
[初步尝试]
小亮同学在对这一图形进行研究时,发现如下事实:
⑴当 时,有EF= ;
⑵当 时,有EF= .
该同学思考研究(2)的过程如下:
作DG∥BC,交AB于G,作DM⊥AB于点M,交EF于点N.
显然HF=CD=b,AG=AB﹣CD=a﹣b.
易证,△DEH∽△DAG,可得 = ,
即, =
而由 ,得 = ,
代入上式,则 = .
解得EH= (a﹣b)
∴EF=EH+HF=b+ (a﹣b)=
[类比发现]
沿用上述图形和已知条件,请自主完成进一步的研究发现:
当 时,EF=;
当 时,EF=;
当 时,EF=;
当 时,EF= . (其中m、n均为正整数,下同)
[推广证明]
当 时,EF=;
请证明你的结论.
[实际应用]
请结合所给情景,创设一个需要采用下面的全部信息求解的问题.
[情景]
如图2,有一块四边形耕地ABCD,AD∥BC,AD=100米,BC=300米,AB=500米,在AB上取点E,使AE=200米,以点E处为起点开挖平行于两底的水渠EF,与CD边相交于点F.
[问题]
?(提问即可,不必求解)
24. 如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为ts(0<t<5).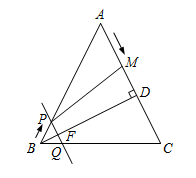 (1)、当t为何值时,四边形PQCM是平行四边形?(2)、设四边形PQCM的面积为ycm2 , 求y与t之间的函数关系式;(3)、是否存在某一时刻t,使S四边形PQCM= S△ABC?若存在,求出t的值;若不存在,说明理由;(4)、连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
(1)、当t为何值时,四边形PQCM是平行四边形?(2)、设四边形PQCM的面积为ycm2 , 求y与t之间的函数关系式;(3)、是否存在某一时刻t,使S四边形PQCM= S△ABC?若存在,求出t的值;若不存在,说明理由;(4)、连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.