山东省青岛市黄岛区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
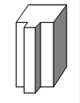
1. 画出如图所示几何体的主视图、左视图和俯视图,其中正确的是( )
 A、
A、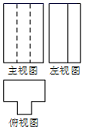 B、
B、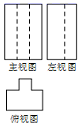 C、
C、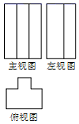 D、
D、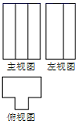 2. 如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
2. 如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )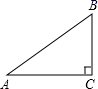 A、sinA= B、tanA= C、cosB= D、tanB=3. 小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最短的时刻为( )A、上午12时 B、上午10时 C、上午9时30分 D、上午8时4. 二次函数 的图象与x轴的交点个数有( )A、0个 B、1个 C、2个 D、无法判断5. 在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为2∶1,把△EFO缩小,则点E的对应点E′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣8,4)或(8,﹣4) D、(﹣2,1)或(2,﹣1)6. 如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF.若 , ,则EF的长为( )
A、sinA= B、tanA= C、cosB= D、tanB=3. 小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最短的时刻为( )A、上午12时 B、上午10时 C、上午9时30分 D、上午8时4. 二次函数 的图象与x轴的交点个数有( )A、0个 B、1个 C、2个 D、无法判断5. 在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为2∶1,把△EFO缩小,则点E的对应点E′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣8,4)或(8,﹣4) D、(﹣2,1)或(2,﹣1)6. 如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF.若 , ,则EF的长为( )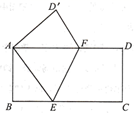 A、 B、 C、 D、7. 如图,将 沿BC方向平移得到 ,AC与DE相交于点G.已知 的面积为18, ,则 与 重叠部分(即 )的面积为( )
A、 B、 C、 D、7. 如图,将 沿BC方向平移得到 ,AC与DE相交于点G.已知 的面积为18, ,则 与 重叠部分(即 )的面积为( )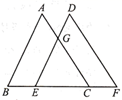 A、6 B、8 C、9 D、128. 已知点 , 是反比例函数 的图象上的两点,且当 时, ,则函数 与 在同一直角坐标系中的图象可能是( )A、
A、6 B、8 C、9 D、128. 已知点 , 是反比例函数 的图象上的两点,且当 时, ,则函数 与 在同一直角坐标系中的图象可能是( )A、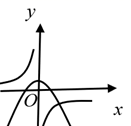 B、
B、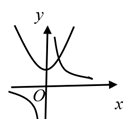 C、
C、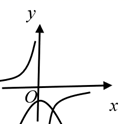 D、
D、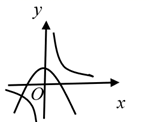
二、填空题
-
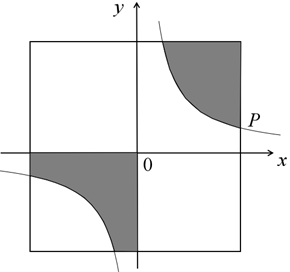
9. 计算: .10. 一个不透明的口袋中装有若干个红球,小明又放入10个黑球,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程后发现,摸到黑球的频率稳定在0.4左右,则估计口袋中红球的数量为个.11. 如图,正方形的中心在直角坐标系的原点,正方形的边与坐标轴平行,点 是正方形与反比例函数图象的一个交点.已知图中阴影部分的面积等于18,则这个反比例函数的表达式为 .
 12. 为庆祝嫦娥五号登月成功,某工艺厂生产了一款纪念品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就多售出5件,但要求销售单价不得低于成本.则该工艺厂将每件的销售价定为元时,可使每天所获销售利润最大.13. 如图,在菱形ABCD中, , ,E,F分别是CD和BC的中点,连接EF并延长与AB的延长线相交于点G,则EG的长度为cm.
12. 为庆祝嫦娥五号登月成功,某工艺厂生产了一款纪念品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就多售出5件,但要求销售单价不得低于成本.则该工艺厂将每件的销售价定为元时,可使每天所获销售利润最大.13. 如图,在菱形ABCD中, , ,E,F分别是CD和BC的中点,连接EF并延长与AB的延长线相交于点G,则EG的长度为cm.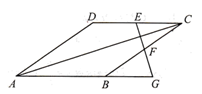 14. 如图,四边形 是矩形,延长 到点 ,使 ,连接 ,点 是 的中点,连接 , ,得到 ;点 是 的中点,连接 , ,得到 ;点 是 的中点,连接 , ,得到 ;…;按照此规律继续进行下去,若矩形 的面积等于2,则 的面积为 . (用含正整数 的式子表示)
14. 如图,四边形 是矩形,延长 到点 ,使 ,连接 ,点 是 的中点,连接 , ,得到 ;点 是 的中点,连接 , ,得到 ;点 是 的中点,连接 , ,得到 ;…;按照此规律继续进行下去,若矩形 的面积等于2,则 的面积为 . (用含正整数 的式子表示)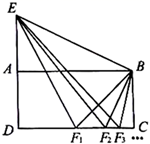
三、解答题
-
15. 已知:如图,线段a.求作:正方形ABCD,使正方形ABCD的对角线AC=a.
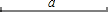 16.(1)、解方程: ;(2)、求二次函数 的图象与一次函数 的图象的交点坐标.17. 祖国至上、团结协作、顽强拼搏、永不言败,女排精神代代流传.中国女排一路都在创造奇迹,书写中国人的传奇….2020年9月,电影《夺冠》正式上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用摸球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个不透明的袋子中装有编号为1,2,3的三个小球(除编号外都相同).从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和为奇数,则小亮胜,若两次数字之和为偶数,则小丽胜.(1)、请用列表或画树状图的方法表示摸球所有可能出现的结果;(2)、这个游戏对双方公平吗?请说明理由.18. 为改善村容村貌,建设美丽乡村,某村计划将一块长18米、宽10米的矩形场地建成绿化广场.如图,广场内部修建同样宽的三条小路,其中一条路与广场的长边平行,另两条路与广场的短边平行,其余区域进行绿化,使绿化区域的面积为广场总面积的80%,小路的宽应为多少米?
16.(1)、解方程: ;(2)、求二次函数 的图象与一次函数 的图象的交点坐标.17. 祖国至上、团结协作、顽强拼搏、永不言败,女排精神代代流传.中国女排一路都在创造奇迹,书写中国人的传奇….2020年9月,电影《夺冠》正式上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用摸球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个不透明的袋子中装有编号为1,2,3的三个小球(除编号外都相同).从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和为奇数,则小亮胜,若两次数字之和为偶数,则小丽胜.(1)、请用列表或画树状图的方法表示摸球所有可能出现的结果;(2)、这个游戏对双方公平吗?请说明理由.18. 为改善村容村貌,建设美丽乡村,某村计划将一块长18米、宽10米的矩形场地建成绿化广场.如图,广场内部修建同样宽的三条小路,其中一条路与广场的长边平行,另两条路与广场的短边平行,其余区域进行绿化,使绿化区域的面积为广场总面积的80%,小路的宽应为多少米? 19. 为增强身体素质,小明和爸爸绕着小区广场锻炼,如图,在矩形广场ABCD边AB的中点M处有一座雕塑.在某一时刻,小明到达点P处,爸爸到达点Q处,此时雕塑在小明的南偏东42°方向,爸爸在小明的北偏东67°方向,若小明离开A点的距离 ,求小明与爸爸的距离PQ.(参考数据: , , , , , )
19. 为增强身体素质,小明和爸爸绕着小区广场锻炼,如图,在矩形广场ABCD边AB的中点M处有一座雕塑.在某一时刻,小明到达点P处,爸爸到达点Q处,此时雕塑在小明的南偏东42°方向,爸爸在小明的北偏东67°方向,若小明离开A点的距离 ,求小明与爸爸的距离PQ.(参考数据: , , , , , )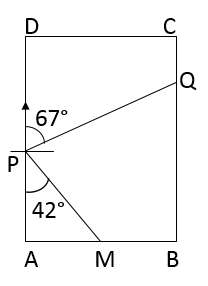 20. 如图,一次函数y x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y (x<0)的图象交于点C(﹣2,2).
20. 如图,一次函数y x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y (x<0)的图象交于点C(﹣2,2). (1)、求一次函数与反比例函数的表达式;(2)、过点B作x轴的平行线交反比例函数的图象于点D,连接CD.求△BCD的面积.21. 如图,在 中,对角线AC与BD相交于点O,点E,F在BD上,且 ,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)、求一次函数与反比例函数的表达式;(2)、过点B作x轴的平行线交反比例函数的图象于点D,连接CD.求△BCD的面积.21. 如图,在 中,对角线AC与BD相交于点O,点E,F在BD上,且 ,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.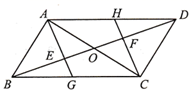 (1)、求证: ;(2)、若AC平分 ,判断四边形AGCH的形状,并证明你的结论.22. 为促进经济发展,方便居民出行.某施工队要修建一个横断面为抛物线的公路隧道.抛物线的最高点P离路面OM的距离为6m,宽度OM为12m.
(1)、求证: ;(2)、若AC平分 ,判断四边形AGCH的形状,并证明你的结论.22. 为促进经济发展,方便居民出行.某施工队要修建一个横断面为抛物线的公路隧道.抛物线的最高点P离路面OM的距离为6m,宽度OM为12m.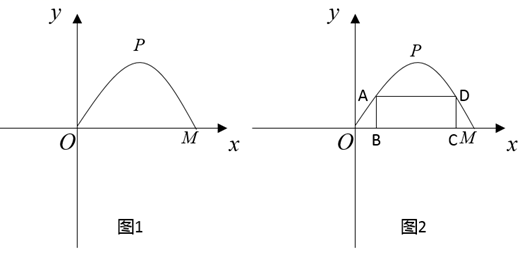 (1)、按如图所示的平面直角坐标系,求表示该抛物线的函数表达式;(2)、一货运汽车装载某大型设备后高为4m,宽为3.5m.如果该隧道内设双向行车道(正中间是一条宽1m的隔离带),那么这辆货车能否安全通过?(3)、施工队计划在隧道口搭建一个矩形“脚手架”ABCD,使A,D点在抛物线上.B,C点在地面OM线上(如图2所示).为了筹备材料,需求出“脚手架”三根支杆AB,AD,DC的长度之和的最大值是多少?请你帮施工队计算一下.23. (问题提出)
(1)、按如图所示的平面直角坐标系,求表示该抛物线的函数表达式;(2)、一货运汽车装载某大型设备后高为4m,宽为3.5m.如果该隧道内设双向行车道(正中间是一条宽1m的隔离带),那么这辆货车能否安全通过?(3)、施工队计划在隧道口搭建一个矩形“脚手架”ABCD,使A,D点在抛物线上.B,C点在地面OM线上(如图2所示).为了筹备材料,需求出“脚手架”三根支杆AB,AD,DC的长度之和的最大值是多少?请你帮施工队计算一下.23. (问题提出)在由 个小正方形(边长为1)组成的矩形网格中,该矩形的一条对角线所穿过的小正方形个数与m,n有何关系?
(问题探究)
为探究规律,我们采用一般问题特殊化的策略,通过分类讨论,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
(1)、探究一:当m,n互质(m,n除1外无其他公因数)时,观察图1并完成下表:
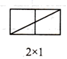
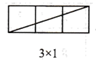
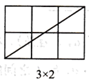
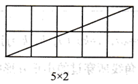
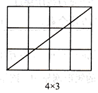
图1
矩形横长m
2
3
3
5
4
5
…
公矩形纵长n
1
1
2
2
3
3
…
矩形一条对角线所穿过的小正方形个数f
2
3
4
6
6
…
结论:当m,n互质时,在 的矩形网格中,该矩形一条对角线所穿过的小正方形的个数f与m,n之间的关系式是 .
(2)、探究二:当m,n不互质时,不妨设 , (a,b,k为正整数,且a,b互质),观察图2并完成下表:
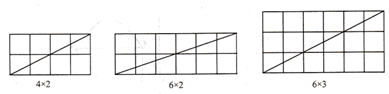
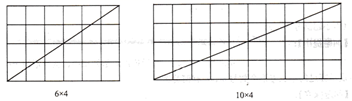
图2
a
2
3
3
5
2
3
…
b
1
1
2
2
1
1
…
k
2
2
2
2
3
…
矩形一条对角线所穿过的小正方形个数f
4
6
8
6
…
结论:当m,n不互质时,若 , (a,b,k为正整数,且a,b互质).在 的矩形网格中,该矩形一条对角线所穿过的小正方形的个数f与a,b,k之间的关系式是 .
(3)、(模型应用)一个由边长为1的小正方形组成的长为630,宽为490的矩形网格中,该矩形的一条对角线所穿过的小正方形个数是个.
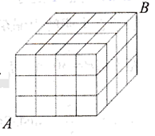
图3
(4)、(模型拓展)如图3,在一个由48个棱长为1的小正方体组成的长方体中,经过顶点A,B的直线穿过的小正方体的个数是个.
24. 如图,在矩形ABCD中, , ,对角线AC,BD交于点O.动点P从点B开始沿BC边以2cm/s的速度运动,动点Q从点A开始沿AD边以lcm/s的速度运动,过点Q作 ,QM交CD于点M,交BD于点N,点E,F分别是PQ,PM与AC的交点.点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动.设动点的运动时间为ts,解答下列问题: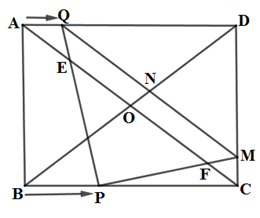 (1)、当t为何值时, ?(2)、设 的面积为 ,写出S与t的关系式;(3)、是否存在某一时刻,使AC将 分成 和四边形EFMQ面积比为 ?若存在,求出t的值;若不存在,请说明理由;(4)、是否存在某一时刻t,使NP平分 ?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时, ?(2)、设 的面积为 ,写出S与t的关系式;(3)、是否存在某一时刻,使AC将 分成 和四边形EFMQ面积比为 ?若存在,求出t的值;若不存在,请说明理由;(4)、是否存在某一时刻t,使NP平分 ?若存在,求出t的值;若不存在,请说明理由.