山东省青岛市城阳区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 两个形状相同、大小相等的小木块放置于桌面上,则其左视图是( )
 A、
A、 B、
B、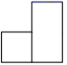 C、
C、 D、
D、 2. 如图,在Rt△ABC中,∠C=90°,BC= ,AB=2,则下列结论正确的是( )
2. 如图,在Rt△ABC中,∠C=90°,BC= ,AB=2,则下列结论正确的是( ) A、 B、 C、 D、3. 小丽和小强在阳光下行走,小丽身高1.6米,她的影长2.0米,小丽比小强矮10cm,此刻小强的影长是( )米.A、 B、 C、 D、4. 在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球,通过多次摸球试验后,发现摸到白球的频率约为30%,估计袋中黑球有( )个.A、8 B、9 C、14 D、155. 方程2 -5 + =0没有实数根,则 的取值范围是( )A、 > B、 < C、 ≤ D、 ≥6. 如图,▱ABCD中,O是对角线AC、BD的交点,△ABO是等边三角形,若AC=8cm,则平行四边形ABCD的面积是( )cm2 .
A、 B、 C、 D、3. 小丽和小强在阳光下行走,小丽身高1.6米,她的影长2.0米,小丽比小强矮10cm,此刻小强的影长是( )米.A、 B、 C、 D、4. 在一个不透明的袋子中有除颜色外均相同的6个白球和若干黑球,通过多次摸球试验后,发现摸到白球的频率约为30%,估计袋中黑球有( )个.A、8 B、9 C、14 D、155. 方程2 -5 + =0没有实数根,则 的取值范围是( )A、 > B、 < C、 ≤ D、 ≥6. 如图,▱ABCD中,O是对角线AC、BD的交点,△ABO是等边三角形,若AC=8cm,则平行四边形ABCD的面积是( )cm2 .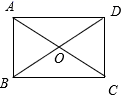 A、16 B、4 C、8 D、167. 某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地.当人和木板对湿地的压力一定时,人和木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图,点A在反比例函数图象上,坐标是(8,30),当压强p(Pa)是4800Pa时,木板面积为( )m2
A、16 B、4 C、8 D、167. 某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地.当人和木板对湿地的压力一定时,人和木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图,点A在反比例函数图象上,坐标是(8,30),当压强p(Pa)是4800Pa时,木板面积为( )m2 A、0.5 B、2 C、0.05 D、208. 如图,在▱ABCD中,AB=6,BC=9,∠ABC,∠BCD的角平分线分别交AD于E和F,BE与CF交于点O,则△EFO与△BCO面积之比是( )
A、0.5 B、2 C、0.05 D、208. 如图,在▱ABCD中,AB=6,BC=9,∠ABC,∠BCD的角平分线分别交AD于E和F,BE与CF交于点O,则△EFO与△BCO面积之比是( ) A、1∶3 B、1∶9 C、2∶3 D、9∶1
A、1∶3 B、1∶9 C、2∶3 D、9∶1二、填空题
-
9. 计算:tan45°+ sin60°= .10. 由于手机市场的迅速成长,某品牌的手机为了赢得消费者,在一年之内连续两次降价,从5980元降到4698元,如果每次降低的百分率相同,求每次降低的百分率是多少?设这个降低百分率为 ,则根据题意,可列方程: .11. 如图,△ABC中,D、E分别是AB、AC上的点,且DE//BC,若AD=6,DB=8,AE=4,则AC= .
 12. 在平面直角坐标系中,已知点A(﹣4,﹣4),B(﹣6,2),以原点O为位似中心,位似比为2∶1,将△ABO缩小,则点B的对应点B′的坐标是 .13. 如图所示,某小区想借助互相垂直的两面墙(墙体足够长),在墙角区域40m长的篱笆围成一个面积为384m2矩形花园.设宽AB= m,且AB<BC,则 =m.
12. 在平面直角坐标系中,已知点A(﹣4,﹣4),B(﹣6,2),以原点O为位似中心,位似比为2∶1,将△ABO缩小,则点B的对应点B′的坐标是 .13. 如图所示,某小区想借助互相垂直的两面墙(墙体足够长),在墙角区域40m长的篱笆围成一个面积为384m2矩形花园.设宽AB= m,且AB<BC,则 =m. 14. 如图,在水平的地面BD上有两根与地面垂直且长度相等的电线杆AB,CD,以点B为坐标原点,直线BD为 轴建立平面直角坐标系.已知电线杆之间的电线可近似地看成抛物线 则电线最低点离地面的距离是米.
14. 如图,在水平的地面BD上有两根与地面垂直且长度相等的电线杆AB,CD,以点B为坐标原点,直线BD为 轴建立平面直角坐标系.已知电线杆之间的电线可近似地看成抛物线 则电线最低点离地面的距离是米. 15. 已知二次函数 的图象如图所示,它与 轴的两个交点的坐标分别为(﹣1,0)(2,0).下列结论:① ;② ;③当 时, ;④当﹣1< <2时, <0.正确的有 . (填正确结论的序号).
15. 已知二次函数 的图象如图所示,它与 轴的两个交点的坐标分别为(﹣1,0)(2,0).下列结论:① ;② ;③当 时, ;④当﹣1< <2时, <0.正确的有 . (填正确结论的序号).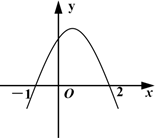 16. 如图,在菱形ABCD中,对角线AC=8cm,BD=4cm, AC,BD相交于点O,过点A作AE⊥CD交CD的延长线于点E,过点O作OF⊥AE交AE于点F,下列结论:①tan∠FOA= ; ② ;③ cm;④S梯形ABCE= cm2 . 正确的有 . (填正确结论的序号).
16. 如图,在菱形ABCD中,对角线AC=8cm,BD=4cm, AC,BD相交于点O,过点A作AE⊥CD交CD的延长线于点E,过点O作OF⊥AE交AE于点F,下列结论:①tan∠FOA= ; ② ;③ cm;④S梯形ABCE= cm2 . 正确的有 . (填正确结论的序号).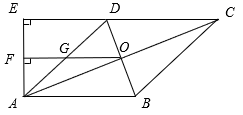
三、解答题
-
17. 已知:线段 .
求作:正方形ABCD,使正方形ABCD边长AB= .
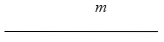 18. 解方程:(1)、 (用配方法).(2)、 (用适当方法).19. 在一个不透明的盒子里,装有四个分别标有数字3、-3、6、-6的小球,小球的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为 ,放回盒子摇匀后,再由小华随机取出一个小球,记下数字为 .(1)、用列表法或树状图法表示出( , )所有可能出现的结果;(2)、求小明、小华各取一次小球所确定的数字和为0的概率.20. 如图,在矩形ABOC中,AB=4,AC=6,点D是边AB的中点,反比例函数 ( <0)的图象经过点D,交AC边于点E,直线DE的关系式为 =m +n(m≠0).
18. 解方程:(1)、 (用配方法).(2)、 (用适当方法).19. 在一个不透明的盒子里,装有四个分别标有数字3、-3、6、-6的小球,小球的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为 ,放回盒子摇匀后,再由小华随机取出一个小球,记下数字为 .(1)、用列表法或树状图法表示出( , )所有可能出现的结果;(2)、求小明、小华各取一次小球所确定的数字和为0的概率.20. 如图,在矩形ABOC中,AB=4,AC=6,点D是边AB的中点,反比例函数 ( <0)的图象经过点D,交AC边于点E,直线DE的关系式为 =m +n(m≠0).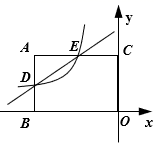 (1)、求反比例函数的关系式和直线DE的关系式;(2)、在第二象限内,根据图象直接写出当 时, .21. 为全面实施乡村振兴战略,促进农业全面升级、农村全面进步、农民全面发展.如图,四边形ABCD是某蔬菜大棚的侧面示意图,已知墙BC与地面垂直,且长度为5米,现测得∠ABC=112°,∠D=67°,AB=4米,求此蔬菜大棚的宽CD的长度.(精确到0.1米)(参考数据:sin22°≈ ,cos22°≈ ,tan22°≈ ,sin67°≈ ,cos67°≈ ,tan67°≈ )
(1)、求反比例函数的关系式和直线DE的关系式;(2)、在第二象限内,根据图象直接写出当 时, .21. 为全面实施乡村振兴战略,促进农业全面升级、农村全面进步、农民全面发展.如图,四边形ABCD是某蔬菜大棚的侧面示意图,已知墙BC与地面垂直,且长度为5米,现测得∠ABC=112°,∠D=67°,AB=4米,求此蔬菜大棚的宽CD的长度.(精确到0.1米)(参考数据:sin22°≈ ,cos22°≈ ,tan22°≈ ,sin67°≈ ,cos67°≈ ,tan67°≈ )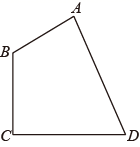 22. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,DE⊥AC,BF⊥AC,垂足分别为E、F.延长BF至G,使FG=BF,连结DG.
22. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,DE⊥AC,BF⊥AC,垂足分别为E、F.延长BF至G,使FG=BF,连结DG. (1)、求证:GF=DE.(2)、当OF∶BF=1∶2时,判断四边形DEFG是什么特殊四边形?并说明理由.23. “互联网+”时代,网上购物备受消费者青睐.越来越多的人可以足不出户就能进行网上购物,网上支付,中国电子商务的发展走在了世界的前列.某网店专售一种书包,其成本为每个40元,已知销售过程中,当售价为每个50元时,每月可销售500个.据市场调查发现,销售单价每涨2元,每月就少售20个.物价部门规定:销售单价不低于成本单价,且这种商品的利润率不得高于60%.设每个书包售 元,每月销售量 个.(1)、求出 与 的函数关系式;(2)、设该网店每月获得的利润为W元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出100元资助贫困学生.为了保证捐款后每月获得的利润不低于6650元,且让消费者得到最大的实惠,如何确定该商品的销售单价?24.
(1)、求证:GF=DE.(2)、当OF∶BF=1∶2时,判断四边形DEFG是什么特殊四边形?并说明理由.23. “互联网+”时代,网上购物备受消费者青睐.越来越多的人可以足不出户就能进行网上购物,网上支付,中国电子商务的发展走在了世界的前列.某网店专售一种书包,其成本为每个40元,已知销售过程中,当售价为每个50元时,每月可销售500个.据市场调查发现,销售单价每涨2元,每月就少售20个.物价部门规定:销售单价不低于成本单价,且这种商品的利润率不得高于60%.设每个书包售 元,每月销售量 个.(1)、求出 与 的函数关系式;(2)、设该网店每月获得的利润为W元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出100元资助贫困学生.为了保证捐款后每月获得的利润不低于6650元,且让消费者得到最大的实惠,如何确定该商品的销售单价?24.⑴阅读下面的材料:
如果函数 =f( )满足:对于自变量x的取值范围内的任意 , ,
①若 < ,都有f( )<f( ),则称f( )是增函数;
②若 < ,都有f( )>f( ),则称f( )是减函数.
例题:证明函数f( )= ( >0)是减函数.
证明:设0< < ,
f( )﹣f( )= = = .
∵0< < ,
∴ ﹣ >0, >0.
∴ >0.即f( )﹣f( )>0.
∴f( )>f( ).
∴函数f( )= ( >0)是减函数.
⑵根据以上材料,解答下面的问题:
已知:函数f( )= ( <0),
①计算:f(﹣1)= ▲ , f(﹣2)= ▲ ;
②猜想:函数f( )= ( <0)是 ▲ 函数(填“增”或“减”);
③验证:请仿照例题证明你对②的猜想.
25. 如图,矩形ABCD中,AB=4cm,AD=5cm,E是AD上一点,DE=3cm,连接BE、CE.点P从点C出发,沿CE方向向点E匀速运动,运动速度2cm/s,同时点Q从点B出发,沿BC方向匀速运动,运动速度均为1cm/s,连接PQ. 设点P、Q的运动时间为t(s)(0<t<2.5).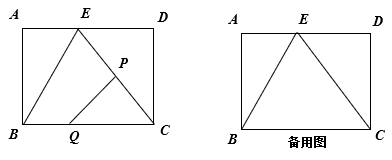 (1)、当t为何值时,△PQC是等腰三角形?(2)、设五边形ABQPE的面积为 (cm2),求 与t之间的函数关系式.(3)、是否存在某一时刻t,使得S五边形ABQPE∶S矩形ABCD=23∶50?若存在,求出t的值,并求出此时PQ的长;若不存在,请说明理由.
(1)、当t为何值时,△PQC是等腰三角形?(2)、设五边形ABQPE的面积为 (cm2),求 与t之间的函数关系式.(3)、是否存在某一时刻t,使得S五边形ABQPE∶S矩形ABCD=23∶50?若存在,求出t的值,并求出此时PQ的长;若不存在,请说明理由.