山东省临沂市沂水县2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件中，必然事件是（）

A、未来一周都是好天气 B、假期出门遇见同学 C、不在同一直线上的三个点确定一个圆 D、掷一次硬币，正面向上

查看试题解析
2. 方程x（x﹣5）＝2（x﹣5）的解是（）

A、﹣5 B、2 C、2或﹣5 D、2或5

查看试题解析
3. 如图，将△AOB绕点O按逆时针方向旋转50°后得到△COD，若∠AOB＝15°，则∠BOC的度数是（）

A、35° B、45° C、55° D、65°

查看试题解析
4. 抛物线y＝2x²﹣5x+1的对称轴是直线（）

A、x＝ $\frac{5}{2}$ B、x＝ $\frac{5}{4}$ C、x＝﹣ $\frac{5}{2}$ D、x＝﹣ $\frac{5}{4}$

查看试题解析
5. 在掷硬币的实验中，正确的是（）

A、老师安排每位同学回家做实验，硬币自由选取 B、老师安排同学回家做实验，硬币统一发（完全一样的）．同学交来的结果，老师挑选他满意的进行统计，他不满意的就不要 C、甲做了2000次，得出正面向上的机率是46%，于是他断定在做第2001次时，正面不会向上 D、乙认为一次一次做，速度太慢，他拿来了大量完全一样的硬币，随意朝上轻轻抛出，然后统计正面向上的次数，这样大大提高了速度

查看试题解析
6. 如图，在△ABC中，DE∥BC，AD＝5，AB＝12，AE＝3，则EC的长是（）

A、 $\frac{36}{5}$ B、 $\frac{21}{5}$ C、20 D、15

查看试题解析
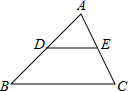7. 在△ABC中，已知∠C＝90°，AC＝4 $\sqrt{5}$ ，sinA＝ $\frac{2}{3}$ ，那么BC边的长是（）

A、2 $\sqrt{5}$ B、8 C、4 $\sqrt{5}$ D、12

查看试题解析
8. 在温度不变的条件下，气体的压强和气体体积对应数值如下表，则可以反映y与x之间的关系的式子是（）

体积x（mL）

100

80

60

40

20

压强y（kPa）

60

75

100

150

300

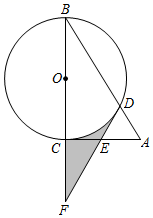
A、y＝6000x B、y＝3000x C、y＝ $\frac{6000}{x}$ D、y＝ $\frac{3000}{x}$

查看试题解析
9. 如图，点A，B，C在⊙O上，点D是AB延长线上一点，若∠AOC＝110°，则∠CBD的度数为（）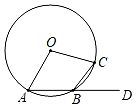

A、50° B、52.5° C、55° D、62.5°

查看试题解析
10. 如图，电线杆的高度为CD＝m，两根拉线AC与BC互相垂直（A，D，B在同一条直线上），若∠CBA＝α，则拉线AC的长度可以表示为（）

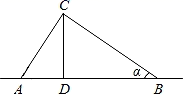A、 $\frac{m}{\sin α}$ B、 $\frac{m}{\cos α}$ C、mcosα D、 $\frac{m}{\tan α}$

查看试题解析
11. 《孙子算经》是我国古代重要的数学著作，其有题译文如下：“有一根竹竿在太阳下的影子长 $15$ 尺.同时立一根 $1.5$ 尺的小标杆，它的影长是 $0.5$ 尺。如图所示，则可求得这根竹竿的长度为（）尺

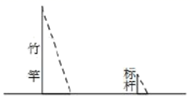A、50 B、45 C、5 D、4.5

查看试题解析
12. 某商场降价销售一批名牌衬衫，已知所获利润y(元)与降价x(元)之间的关系是y=-2x²+60x+800，则利润获得最多为（）

A、15元 B、400元 C、800元 D、1250元

查看试题解析
13. 如图，已知⊙O上三点A，B，C，∠ABC＝15°，切线PA交OC延长线于点P，AP＝ $\sqrt{3}$ ，则⊙O的半径为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\sqrt{3}$ D、3

查看试题解析
14. 已知函数 $y = \frac{m}{x}$ 的图象如图，以下结论：①m＜0；②在每个分支上y随x的增大而增大；③若点A（﹣1，a），点B（2，b）在图象上，则a＜b；④若点P（x，y）在图象上，则点P₁（﹣x，﹣y）也在图象上．其中正确的个数是（）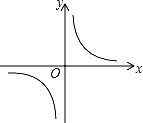

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

15. 反比例函数 $y = \frac{k}{x}$ 经过（﹣2，2），则图象在象限．

查看试题解析
16. 在十字路口，汽车可直行、左转、右转，三种可能性相同，则一辆汽车经过向右转的概率为．

查看试题解析
17. 如图，在正方形网格中，△ABC的顶点都在格点上，则tan∠ABC的值为．

查看试题解析
18. 如图，在△ABC中，点D，E分别在边AB，AC上，且DE∥BC，若S_△ADE＝S_{四边形DBCE} ，则 $\frac{B D}{A D}$ ＝．

查看试题解析
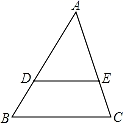19. 已知圆锥的侧面展开的扇形面积是6π，圆心角是60°，则这个圆锥的底面圆的半径是．

查看试题解析

三、解答题

20. 九年级（1）班在两名男生和一名女生中任选两人参加学校组织的演讲比赛．请用画树状图或列表的方法求两人都是男生的概率．

查看试题解析
21. 某商场在春节期间将单价200元的某种商品经过两次降价后，以162元的价格出售．

(1)、求平均每次降价的百分率；

(2)、售货员向经理建议：先公布降价5%，再下调15%，这样更有吸引力，请问售货员的方案对顾客是否更优惠？为什么？

查看试题解析
22. 如图，在平行四边形ABCD中，E为AB边上一点，连接CE，F为CE上一点，且∠DFE＝∠A．

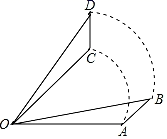
(1)、求证：△DCF∽△CEB；

(2)、若AD＝6，CD＝8，DF＝4，求CE的长．

查看试题解析
23. 已知点P是 $\overset{⌢}{A B}$ 上的一个动点，∠APB＝118°，AB＝10，点P到AB的最大距离约为多少？（结果保留整数，参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60．）

查看试题解析
24. 如图，已知直线y₁＝x+m与x轴、y轴分别交于点A，B，与双曲线y₂＝ $\frac{k}{x}$ （x＜0）分别交于点C，D，且点C的坐标为（﹣1，4）．

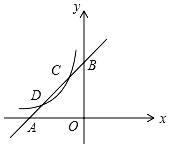(1)、分别求直线、双曲线的函数表达式；

(2)、求点D的坐标；

(3)、利用函数图象直接写出：当x在什么范围内取值时y₂＜y₁ ．

查看试题解析
25. 如图，在Rt△ABC中，∠ACB=90°，以直角边BC为直径的⊙O交斜边AB于点D．点E为边AC的中点，连接DE并延长交BC的延长线于点F．

(1)、求证：直线DE是⊙O的切线；

(2)、若∠B=30°，AC=4，求阴影部分的面积．

查看试题解析
26. 已知直线x＝1是抛物线y＝ax²+bx+c（a，b，c是常数，a≠0）的对称轴．

(1)、若抛物线顶点在x轴上，且过（0，1），求抛物线的解析式；

(2)、若抛物线不过第一象限，求 $\frac{c}{a}$ 的取值范围；

(3)、若抛物线过点（1，1），当﹣1≤x≤0时，抛物线上的点到x轴距离的最大值为4，求a的值．

查看试题解析

体积x（mL）	100	80	60	40	20
压强y（kPa）	60	75	100	150	300