山东省临沂市沂南县2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. tan45°的值为（）

A、2 B、﹣2 C、1 D、﹣1

查看试题解析
2. 下列事件中，是必然事件的是（）

A、汽车走过一个红绿灯路口时，前方正好是绿灯 B、任意买一张电影票，座位号是3的倍数 C、掷一枚质地均匀的硬币，正面向上 D、从一个只有白球的盒子里摸出一个球是白球

查看试题解析
3. 在平面直角坐标系中，点 $(3, 2)$ 关于原点对称的点的坐标是（）

A、 $(2, 3)$ B、 $(- 3, 2)$ C、 $(- 3, - 2)$ D、 $(- 2, - 3)$

查看试题解析
4. 如图是由5个相同的小正方体搭成的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
5. 李明参加的社区抗疫志愿服务团队共有A、B、C、D四个服务项目，其中每个服务项目又分为第一小组和第二小组，则李明分到A项目的第一小组的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{3}{8}$

查看试题解析
6. 如图，△ABC∽△DCA，∠B＝33°，∠D＝117°，则∠BAD的度数是（）

A、150° B、147° C、135° D、120°

查看试题解析
7. 一元二次方程x²﹣4x＝5的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
8. 已知点A（x₁ ， ﹣4），B（x₂ ， 8）都在反比例函数y＝﹣ $\frac{5}{x}$ 的图象上，则下列关系式一定正确的是（）

A、x₂＜x₁＜0 B、x₁＜0＜x₂ C、x₁＜x₂＜0 D、x₂＜0＜x₁

查看试题解析
9. 如图，从⊙O外一点A引圆的切线AB，切点为B，连接AO并延长交圆于点C，连接BC.若∠A＝28°，则∠ACB的度数是（）

A、28° B、30° C、31° D、32°

查看试题解析
10. 如图， $A 、 B$ 是函数 $y = \frac{1}{x}$ 的图像上关于原点对称的任意两点， $B C // x$ 轴， $A C // y$ 轴， $Δ A B C$ 的面积记为 $S$ ，则（）

A、 $S = 2$ B、 $S = 4$ C、 $2 < S < 4$ D、 $S > 4$

查看试题解析
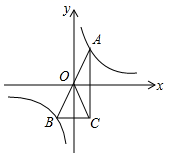11. 某数学兴趣小组来到城关区时代广场，设计用手电来测量广场附近某大厦CD的高度，如图，点P处放一水平的平面镜．光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB＝1.5米，BP＝2米，PD＝52米，那么该大厦的高度约为（）

A、39米 B、30米 C、24米 D、15米

查看试题解析
12. 如图，在平面直角坐标系中，一次函数y=-4x+4的图像与x轴，y轴分别交于A，B两点，正方形ABCD的顶点C，D在第一象限，顶点D在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像上，若正方形ABCD向左平移n个单位后，顶点C恰好落在反比例函数的图象上，则n的值是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 方程 $x^{2} - x = 6$ 的解是．

查看试题解析
14. 在双曲线y＝ $\frac{2 - k}{x}$ 的每一支上，y都随着x的增大而减小，则k的取值范围为.

查看试题解析
15. 如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则sin∠ABC的值为．

查看试题解析
16. 如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AC＝ $\sqrt{3}$ ，∠B＝60°，则CD的长为．

查看试题解析
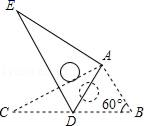17. 如图，在扇形OAB中，∠AOB＝90°，点C为OB的中点，CD⊥OB交弧AB于点D．若OA＝2，则阴影部分的面积为．

查看试题解析
18. 如图，从某建筑物10 m高的窗口A处用水管向外喷水，喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1 m，离地面 $\frac{40}{3}$ m，则水流落地点B离墙的距离OB是.
　　　

查看试题解析

三、解答题

19. 计算：2cos60°+4sin60°•tan30°﹣6cos²45°.

查看试题解析
20. 你吃过拉面吗？在做拉面的过程中渗透着数学知识：一定体积的面团做成拉面，面条的总长度y（m）是面条的横截面积x（mm²）（x＞0）的反比例函数，其图象如图所示．

(1)、请写出点P的实际意义；

(2)、求出y与x的函数关系式；

(3)、当面条的横截面积是1.6mm²时，求面条的总长度．

查看试题解析
21. 如图，某消防队在一居民楼前进行演习，消防员利用云梯成功救出点B处的求救者后，又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°，点A距地面2.5米，点B距地面10.5米.为救出点C处的求救者，云梯需要继续上升的高度BC约为多少米？（结果保留整数.参考数据：tan65°≈2.1，sin65°≈0.9，cos65°≈0.4， $\sqrt{2}$ ≈1.4）

查看试题解析
22. 某商城销售一种进价为10元1件的饰品，经调查发现，该饰品的销售量y（件）与销售单价x（元）满足函数y＝﹣2x+100，设销售这种饰品每天的利润为W（元）．

(1)、求W与x之间的函数表达式；

(2)、当销售单价定为多少元时，该商城获利最大？最大利润为多少？

(3)、在确保顾客得到优惠的前提下，该商城还要通过销售这种饰品每天获利750元，该商城应将销售单价定为多少？

查看试题解析
23. 如图，四边形ABCD内接于⊙O，AC是直径，AB＝BC，连接BD，过点D的直线与CA的延长线相交于点E，且∠EDA＝∠ACD．

(1)、求证：直线DE是⊙O的切线；

(2)、若AD＝6，CD＝8，求BD的长．

查看试题解析
24. 已知△ABC为等边三角形，点D是线段AB上一点（不与A、B重合）．将线段CD绕点C逆时针旋转60°得到线段CE．连结DE、BE．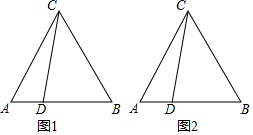

(1)、依题意补全图1并判断AD与BE的数量关系．

(2)、过点A作AF⊥EB交EB延长线于点F．用等式表示线段EB、DB与AF之间的数量关系并证明．

查看试题解析
25. 如图，已知抛物线y＝ax²过点A（﹣3， $\frac{9}{4}$ ）．

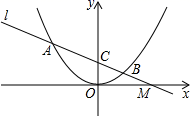(1)、求抛物线的解析式；

(2)、已知直线l过点A ， M（ $\frac{3}{2}$ ，0）且与抛物线交于另一点B ，与y轴交于点C ，求证：MC²＝MA•MB；

(3)、若点P ， D分别是抛物线与直线l上的动点，以OC为一边且顶点为O ， C ， P ， D的四边形是平行四边形，求所有符合条件的P点坐标．

查看试题解析