山东省临沂市平邑县2020-2021学年年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 关于x的一元二次方程x2﹣4x+3=0的解为( )A、x1=﹣1,x2=3 B、x1=1,x2=﹣3 C、x1=1,x2=3 D、x1=﹣1,x2=﹣32. 如图是由5个大小相同的小正方体摆成的几何体,它的俯视图是( )
 A、
A、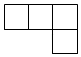 B、
B、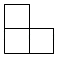 C、
C、 D、
D、 3. 有人预测2020年东京奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该是( ).A、中国女排一定会夺冠 B、中国女排一定不会夺冠 C、中国女排夺冠的可能性比较大 D、中国女排夺冠的可能性比较小4. 二次函数的图象上有两点 和 ,则此拋物线的对称轴是( )A、x=4 B、x=3 C、x=-5 D、x=-15. 若 是方程 的一个根,则 的值为( )A、2020 B、-2020 C、2019 D、-20196. 如图,在 中, 下列三角函数正确的是( )
3. 有人预测2020年东京奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该是( ).A、中国女排一定会夺冠 B、中国女排一定不会夺冠 C、中国女排夺冠的可能性比较大 D、中国女排夺冠的可能性比较小4. 二次函数的图象上有两点 和 ,则此拋物线的对称轴是( )A、x=4 B、x=3 C、x=-5 D、x=-15. 若 是方程 的一个根,则 的值为( )A、2020 B、-2020 C、2019 D、-20196. 如图,在 中, 下列三角函数正确的是( )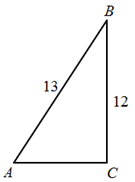 A、 B、 C、 D、7. 如图, 是 的中位线,则 的值为( )
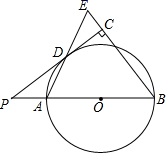
A、 B、 C、 D、7. 如图, 是 的中位线,则 的值为( )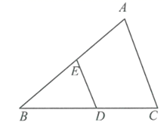 A、 B、 C、 D、8. 如图, 为 的内接三角形,AB为 的直径,点D在 上, ,则 的度数为( ).
A、 B、 C、 D、8. 如图, 为 的内接三角形,AB为 的直径,点D在 上, ,则 的度数为( ). A、 B、 C、 D、9. 下列函数中,当x>0时,y随x的增大而增大的是( )A、 B、 C、 D、10. 如图,在 中, , 于点 ,下列结论中错误的是( )
A、 B、 C、 D、9. 下列函数中,当x>0时,y随x的增大而增大的是( )A、 B、 C、 D、10. 如图,在 中, , 于点 ,下列结论中错误的是( )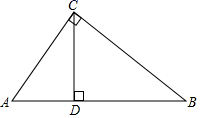 A、 B、 C、 D、11. 如图,等边三角形ABC和正方形ADEF都内接于 ,则 ( )
A、 B、 C、 D、11. 如图,等边三角形ABC和正方形ADEF都内接于 ,则 ( ) A、 B、 C、 D、12. 如图一,在等腰△ABC中,AB=AC,点P、Q从点B同时出发,点P以 cm/s的速度沿BC方向运动到点C停止,点Q以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则y与x之间的函数关系图象如图二所示,则BC长为( )
A、 B、 C、 D、12. 如图一,在等腰△ABC中,AB=AC,点P、Q从点B同时出发,点P以 cm/s的速度沿BC方向运动到点C停止,点Q以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则y与x之间的函数关系图象如图二所示,则BC长为( ) A、4cm B、8cm C、8 D、4
A、4cm B、8cm C、8 D、4二、填空题
-
13. 在△ABC中,若∠A , ∠B满足|cosA- |+(sinB- )2=0,则∠C= .14. 有五张分别印有圆、等腰三角形、矩形、菱形、正方形图案的卡片(卡片中除图案不同外,其余均相同),现将有图案的一面朝下任意摆放,从中任意抽取一张,抽到有中心对称图案的卡片的概率是 .15. 如图, 中, .将 绕点 逆时针旋转得到 ,使点 的对应点 恰好落在边 上,则 的度数是 .
 16. 如图,已知 中,弦 交于 ,则 .
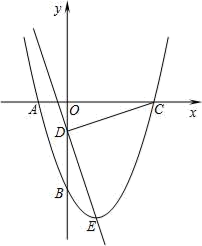
16. 如图,已知 中,弦 交于 ,则 . 17. 如图,过 轴上任意一点 作 轴的平行线,分别与反比例函数 , 的图象交于 点和 点,若 为 轴任意一点.连接 、 ,则 的面积为
17. 如图,过 轴上任意一点 作 轴的平行线,分别与反比例函数 , 的图象交于 点和 点,若 为 轴任意一点.连接 、 ,则 的面积为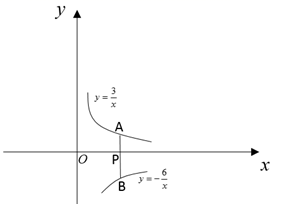 18. 抛物线 上部分点的横坐标 ,纵坐标 的对应值如表所示,下列说法:
18. 抛物线 上部分点的横坐标 ,纵坐标 的对应值如表所示,下列说法:···
-3
-2
-1
0
1
···
···
-6
0
4
6
6
···
①抛物线与 轴的交点为 ;②抛物线的对称轴是在 轴右侧;③在对称轴左侧, 随 增大而减小;④抛物线一定过点 .上述说法正确的是(填序号).
三、解答题
-
19. 小强在地面 处放一面镜子,刚好能从镜子中看到教学楼的顶端 此时 米, 米.已知眼睛距离地面的高度 米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
 20. 已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).(1)、求证:方程有两个不相等的实数根;(2)、设x1 , x2为方程的两个实数根,且x1+2x2=14,试求出方程的两个实数根和k的值.21. 如图,某数学兴趣小组为测量一颗古树 和教学楼 的高,先在 处用高1.5米的测角仪 测得古树顶端 的仰角 为45º,此时教学楼顶端 恰好在视线 上,再向前走10米到达 处,又测得教学楼顶端 的仰角 为 ,点 三点在同一水平线上.
20. 已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).(1)、求证:方程有两个不相等的实数根;(2)、设x1 , x2为方程的两个实数根,且x1+2x2=14,试求出方程的两个实数根和k的值.21. 如图,某数学兴趣小组为测量一颗古树 和教学楼 的高,先在 处用高1.5米的测角仪 测得古树顶端 的仰角 为45º,此时教学楼顶端 恰好在视线 上,再向前走10米到达 处,又测得教学楼顶端 的仰角 为 ,点 三点在同一水平线上. (1)、求古树 的高;(2)、求教学楼 的高.(结果可保留根号)22. 某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作.已知该品牌运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
(1)、求古树 的高;(2)、求教学楼 的高.(结果可保留根号)22. 某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作.已知该品牌运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:第1天
第2天
第3天
第4天
售价x(元/双)
150
200
250
300
销售量y(双)
40
30
24
20
(1)、观察表中数据,x,y满足什么函数关系?写出用x表示y的函数表达式;(2)、若商场计划每天的销售利润为3000元,则每双运动鞋的售价应定为多少元?