山东省临沂市罗庄区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 下面用数学家名字命名的图形中,既是轴对称图形又是中心对称图形的是( )A、
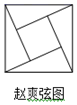 B、
B、 C、
C、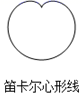 D、
D、 2. 方程x2=x的解是( )A、x1=3,x2=﹣3 B、x1=1,x2=0 C、x1=1,x2=﹣1 D、x1=3,x2=﹣13. 已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( ) .A、 B、 C、 D、4. 二次函数y=x2的图象平移后经过点(2,0),则下列平移方法正确的是( )A、向左平移2个单位,向下平移2个单位 B、向左平移1个单位,向上平移2个单位 C、向右平移1个单位,向下平移1个单位 D、向右平移2个单位,向上平移1个单位5. 已知反比例函数 的图象经过点A(2,2)、B(x,y),当﹣3<x<﹣1时,y的取值范围是( )A、﹣4<y<﹣ B、﹣ <y<﹣4 C、 <y<4 D、﹣1<y<﹣6. 如图, 分别与 相切于 点,C为 上一点, ,则 ( )
2. 方程x2=x的解是( )A、x1=3,x2=﹣3 B、x1=1,x2=0 C、x1=1,x2=﹣1 D、x1=3,x2=﹣13. 已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( ) .A、 B、 C、 D、4. 二次函数y=x2的图象平移后经过点(2,0),则下列平移方法正确的是( )A、向左平移2个单位,向下平移2个单位 B、向左平移1个单位,向上平移2个单位 C、向右平移1个单位,向下平移1个单位 D、向右平移2个单位,向上平移1个单位5. 已知反比例函数 的图象经过点A(2,2)、B(x,y),当﹣3<x<﹣1时,y的取值范围是( )A、﹣4<y<﹣ B、﹣ <y<﹣4 C、 <y<4 D、﹣1<y<﹣6. 如图, 分别与 相切于 点,C为 上一点, ,则 ( )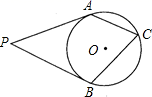 A、 B、 C、 D、7. 如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
A、 B、 C、 D、7. 如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )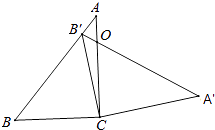 A、50° B、60° C、70° D、80°8. 有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2等于( )
A、50° B、60° C、70° D、80°8. 有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2等于( )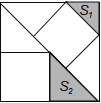 A、1: B、1:2 C、2:3 D、4:99. 如图,以等边△ABC的一边AB为直径的半圆O交AC于点D,交BC于点E,若AB=4,则阴影部分的面积是( )
A、1: B、1:2 C、2:3 D、4:99. 如图,以等边△ABC的一边AB为直径的半圆O交AC于点D,交BC于点E,若AB=4,则阴影部分的面积是( )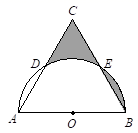 A、2 B、2π C、 D、4π10. 如图,点A是反比例函数y= 的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )
A、2 B、2π C、 D、4π10. 如图,点A是反比例函数y= 的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )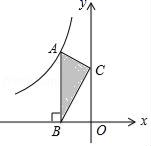 A、4 B、﹣4 C、8 D、﹣811. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为( )
A、4 B、﹣4 C、8 D、﹣811. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为( )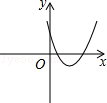 A、
A、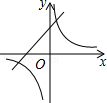 B、
B、 C、
C、 D、
D、 12. 如图,由边长为1的小正方形构成的网格中,点A、B、C都在格点上,以AB为直径的圆经过点C、D,则cos∠ADC的值为( )
12. 如图,由边长为1的小正方形构成的网格中,点A、B、C都在格点上,以AB为直径的圆经过点C、D,则cos∠ADC的值为( ) A、 B、 C、 D、13. 二次函数 的部分图象如图所示,则下列选项错误的是( )
A、 B、 C、 D、13. 二次函数 的部分图象如图所示,则下列选项错误的是( )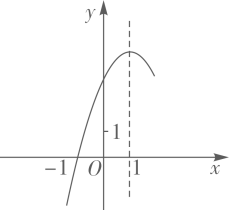 A、若 , 是图象上的两点,则 B、 C、方程 有两个不相等的实数根 D、当 时,y随x的增大而减小14. 如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点 ,点 是 上一动点,点 为弦 的中点,直线 与x轴、y轴分别交于点 ,则 面积的最小值为( )
A、若 , 是图象上的两点,则 B、 C、方程 有两个不相等的实数根 D、当 时,y随x的增大而减小14. 如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点 ,点 是 上一动点,点 为弦 的中点,直线 与x轴、y轴分别交于点 ,则 面积的最小值为( ) A、2 B、2.5 C、 D、
A、2 B、2.5 C、 D、二、填空题
-
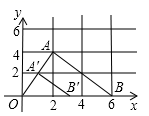
15. 计算:2cos60°+tan45°= .16. 关于x的一元二次方程 有两个不相等的实数根,则q的取值范围是.17. 如图, 三个顶点的坐标分别为 ,以原点O为位似中心,把这个三角形缩小为原来的 ,可以得到 ,已知点 的坐标是 ,则点 的坐标是.
 18. 刘徵是我国古代最杰出的数学家之一,他在《九章算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为 . (参考数据:sin15°=0.26)
18. 刘徵是我国古代最杰出的数学家之一,他在《九章算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为 . (参考数据:sin15°=0.26)
三、解答题
-
19. 如图,四边形OABF中,∠OAB=∠B=90°,点A在x轴上,双曲线 过点F,交AB于点E,连接EF.若 ,S△BEF=4,则k的值为 .
 20. 如图,足球场上守门员在O处开出一记手跑高球,球从地面1.4米的A处抛出(A在y轴上),运动员甲在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面3.2米高,球落地点为C点.
20. 如图,足球场上守门员在O处开出一记手跑高球,球从地面1.4米的A处抛出(A在y轴上),运动员甲在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面3.2米高,球落地点为C点. (1)、求足球开始抛出到第一次落地时,该抛物线的解析式.(2)、足球第一次落地点C距守门员多少米?21. 如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y= (x>0)的图象过点A.
(1)、求足球开始抛出到第一次落地时,该抛物线的解析式.(2)、足球第一次落地点C距守门员多少米?21. 如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y= (x>0)的图象过点A.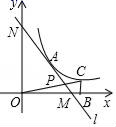 (1)、求直线l和反比例函数的解析式;(2)、在函数y= (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.22. 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上 点处测得树顶端 的仰角为30 ,朝着这棵树的方向走到台阶下的点 处,测得树顶端 的仰角为 .已知 点的高度 为 ,台阶 的倾斜角∠ACB为30°,且 、 、 三点在同一条直线上.请根据以上条件求出树 的高度(测倾器的高度忽略不计).
(1)、求直线l和反比例函数的解析式;(2)、在函数y= (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.22. 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上 点处测得树顶端 的仰角为30 ,朝着这棵树的方向走到台阶下的点 处,测得树顶端 的仰角为 .已知 点的高度 为 ,台阶 的倾斜角∠ACB为30°,且 、 、 三点在同一条直线上.请根据以上条件求出树 的高度(测倾器的高度忽略不计).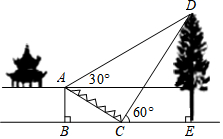 23. 如图,AB是⊙O的弦,半径OE⊥AB,P为AB的延长线上一点,PC与⊙O相切于点C,CE与AB交于点F.
23. 如图,AB是⊙O的弦,半径OE⊥AB,P为AB的延长线上一点,PC与⊙O相切于点C,CE与AB交于点F.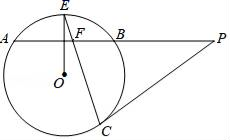 (1)、求证:PC=PF;(2)、连接OB,BC,若OB∥PC,BC=3 ,tanP= ,求FB的长.24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)、求证:PC=PF;(2)、连接OB,BC,若OB∥PC,BC=3 ,tanP= ,求FB的长.24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA. (1)、试求抛物线的解析式;(2)、直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m= ,试求m的最大值及此时点P的坐标.25. 如果三角形的两个内角 与 满足 =90°,那么我们称这样的三角形为“准互余三角形”.
(1)、试求抛物线的解析式;(2)、直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m= ,试求m的最大值及此时点P的坐标.25. 如果三角形的两个内角 与 满足 =90°,那么我们称这样的三角形为“准互余三角形”.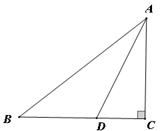 (1)、若△ABC是“准互余三角形”,∠C>90°,∠A=60°,求∠B的度数;(2)、如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5,若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(1)、若△ABC是“准互余三角形”,∠C>90°,∠A=60°,求∠B的度数;(2)、如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5,若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.