山东省临沂市临沭县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 如图图案中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程x2=2x的解是( )A、x=2 B、x=0 C、x1=﹣2,x2=0 D、x1=2,x2=03. 抛物线 的顶点坐标是( )A、(3,1) B、(3,﹣1) C、(﹣3,1) D、(﹣3,﹣1)4. 如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )
2. 一元二次方程x2=2x的解是( )A、x=2 B、x=0 C、x1=﹣2,x2=0 D、x1=2,x2=03. 抛物线 的顶点坐标是( )A、(3,1) B、(3,﹣1) C、(﹣3,1) D、(﹣3,﹣1)4. 如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( ) A、左视图面积最大 B、俯视图面积最小 C、左视图与主视图面积相等 D、俯视图与主视图面积相等5. 如图,AB是 的直径,点 在⊙ 上,若 ,则 ( )
A、左视图面积最大 B、俯视图面积最小 C、左视图与主视图面积相等 D、俯视图与主视图面积相等5. 如图,AB是 的直径,点 在⊙ 上,若 ,则 ( ) A、 B、 C、 D、6. 如图,已知 分别是 的边 上的点,若 ,且 将 分成面积相等的两部分,则 的值为( )
A、 B、 C、 D、6. 如图,已知 分别是 的边 上的点,若 ,且 将 分成面积相等的两部分,则 的值为( ) A、 B、 C、 D、7. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为( )
A、 B、 C、 D、7. 如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为( ) A、 B、 C、 D、8. 若点 , 在反比例函数 的图象上,且 ,则 的取值范围是( )A、 B、 C、 D、 或9. 如图,在 中,点 在边 上,则在下列四个条件中:① ;② ;③ ;④ ,不能判定 与 相似的是( )
A、 B、 C、 D、8. 若点 , 在反比例函数 的图象上,且 ,则 的取值范围是( )A、 B、 C、 D、 或9. 如图,在 中,点 在边 上,则在下列四个条件中:① ;② ;③ ;④ ,不能判定 与 相似的是( ) A、① B、② C、③ D、④10. 在数-1,1,2中任取两个数作为点的坐标,该点刚好在二次函数 图象上的概率是( )A、 B、 C、 D、11. 二次函数 与一次函数 在同一坐标系中的大致图象可能是( )A、
A、① B、② C、③ D、④10. 在数-1,1,2中任取两个数作为点的坐标,该点刚好在二次函数 图象上的概率是( )A、 B、 C、 D、11. 二次函数 与一次函数 在同一坐标系中的大致图象可能是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,从一块半径是2米的圆形铁皮(⊙ )上剪出一个圆心角为60°的扇形(点 在⊙ 上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )米.
12. 如图,从一块半径是2米的圆形铁皮(⊙ )上剪出一个圆心角为60°的扇形(点 在⊙ 上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )米. A、 B、 C、 D、213. 如图,在 中, 是斜边 上两点,且 ,将 绕点 顺时针旋转 后,得到 ,连接 ,下列结论中:① ;② ≌ ;③ 平分 ;④ ;正确的有( )个
A、 B、 C、 D、213. 如图,在 中, 是斜边 上两点,且 ,将 绕点 顺时针旋转 后,得到 ,连接 ,下列结论中:① ;② ≌ ;③ 平分 ;④ ;正确的有( )个 A、1个 B、2个 C、3个 D、4个14. 二次函数 图象的一部分如图所示,顶点坐标为 ,与x轴的一个交点的坐标为 ,给出以下结论:① ;② ;③若 、 为函数图象上的两点,则 ;④当-3 0时方程 有实数根,则t的取值范围是 ,其中正确的结论的个数为( )
A、1个 B、2个 C、3个 D、4个14. 二次函数 图象的一部分如图所示,顶点坐标为 ,与x轴的一个交点的坐标为 ,给出以下结论:① ;② ;③若 、 为函数图象上的两点,则 ;④当-3 0时方程 有实数根,则t的取值范围是 ,其中正确的结论的个数为( )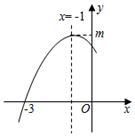 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
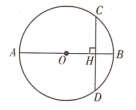
15. 将抛物线 向左平移2个单位,再向下平移1个单位,所得到的抛物线解析式为 .16. 如图,AB为 的直径,弦 于点H , 若 , ,则OH的长度为 .
 17. 如图,在一笔直的海岸线 上有 两个观测站, ,从 测得船 在北偏东45°的方向,从 测得船 在北偏东 的方向,则船 离海岸线 的距离(即 的长)为 .
17. 如图,在一笔直的海岸线 上有 两个观测站, ,从 测得船 在北偏东45°的方向,从 测得船 在北偏东 的方向,则船 离海岸线 的距离(即 的长)为 . 18. 在实数范围内定义一种运算“※”,其运算法则为 ※ = ,根据这个法则,若 ※ ,则 (写成一般式).19. 如图,在Rt△ABC中,∠ACB=90°,AC=BC.点D是线段BC上的一点,连接AD,过点C作CG⊥AD,分别交AD、AB于点G、E,与过点B且垂直于BC的直线相交于点F,连接DE.给出以下四个结论:① ;②若 平分 ,则 ;③若点D是BC的中点,则 ;④若 ,则 .其中正确的结论序号是 .
18. 在实数范围内定义一种运算“※”,其运算法则为 ※ = ,根据这个法则,若 ※ ,则 (写成一般式).19. 如图,在Rt△ABC中,∠ACB=90°,AC=BC.点D是线段BC上的一点,连接AD,过点C作CG⊥AD,分别交AD、AB于点G、E,与过点B且垂直于BC的直线相交于点F,连接DE.给出以下四个结论:① ;②若 平分 ,则 ;③若点D是BC的中点,则 ;④若 ,则 .其中正确的结论序号是 .
三、解答题
-
20.(1)、计算: =(2)、解方程:21. 如图,在平面直角坐标系中, 的三个顶点的坐标分别是 , , .
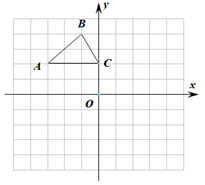
⑴将 以点 为旋转中心旋转180°,画出旋转后对应的 ;
⑵平移 ,若 的对应点 的坐标为 ,画出平移后的 ;
⑶若将 绕某一点旋转可以得到 ,请直接写出旋转中心的坐标.
22. 在一次综合实践活动中,数学兴趣小组的同学想要测量一楼房 的高度.如图,楼房 后有一假山,其斜坡 坡比为1: ,山坡坡面上点 处有一休息亭,在此处测得楼顶 的仰角为45°,假山坡脚 与楼房水平距离 米,与亭子距离 米. (1)、求点 距水平地面 的高度;(2)、求楼房 的高.(结果精确到整数,参考数据 ≈1.414, ≈1.732).23. 如图,在⊙ 中, , ,延长 到 ,使 ,连接 .
(1)、求点 距水平地面 的高度;(2)、求楼房 的高.(结果精确到整数,参考数据 ≈1.414, ≈1.732).23. 如图,在⊙ 中, , ,延长 到 ,使 ,连接 . (1)、求证: 与⊙ 相切;(2)、若 ,求图中阴影部分的面积.(结果保留 和根号)24. 如图,一次函数 与反比例函数 的图象交于 两点.
(1)、求证: 与⊙ 相切;(2)、若 ,求图中阴影部分的面积.(结果保留 和根号)24. 如图,一次函数 与反比例函数 的图象交于 两点. (1)、试求 的值和一次函数的解析式;(2)、根据图象直接写出 的 的取值范围;(3)、求 的面积.25. 数学课上,王老师出示了问题:如图1, , 是四边形 的对角线,若 ,
(1)、试求 的值和一次函数的解析式;(2)、根据图象直接写出 的 的取值范围;(3)、求 的面积.25. 数学课上,王老师出示了问题:如图1, , 是四边形 的对角线,若 ,
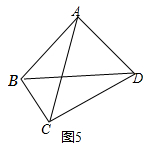
则
(1)、线段 , , 三者之间存在等量关系为:;(2)、经过思考:小丽、小明和小亮三位同学分别展示了三种正确的思路:如图2,在 上取一点 ,使 ,连接 ;
如图3,延长 到 ,使 ,连接 ;
如图4,将 绕着点 逆时针旋转 .
在此基础上,请你选择一种合适的方法证明上述等量关系.
(3)、小强同学提出:如图5,如果把“ ”改为“ ”,其它条件不变,那么线段 , , 三者之间有何等量关系?针对小强提出的问题,请你写出结论,并给出证明.26. 如图,已知抛物线 与x轴交于 , 两点,与y轴交于点C,其顶点为 ,连接 与抛物线的对称轴 交于点 . (1)、求抛物线的表达式并写出该抛物线的对称轴;(2)、在直线 上方的抛物线上找一点 ,使得 的面积最大,求出此时点 的坐标;(3)、点 是对称轴 右侧抛物线上的动点,在射线 上是否存在点 ,使得以点 为顶点的三角形与 相似?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式并写出该抛物线的对称轴;(2)、在直线 上方的抛物线上找一点 ,使得 的面积最大,求出此时点 的坐标;(3)、点 是对称轴 右侧抛物线上的动点,在射线 上是否存在点 ,使得以点 为顶点的三角形与 相似?若存在,求出点 的坐标;若不存在,请说明理由.