山东省临沂市兰山区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨2. 下列图形中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为( )A、1:4 B、4:1 C、1:2 D、2:14. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、5. 如图,OO的弦AB=8,M是AB的中点,且OM=3,则OO的半径等于( )
3. 已知△ABC∽△DEF,且相似比为1:2,则△ABC与△DEF的面积比为( )A、1:4 B、4:1 C、1:2 D、2:14. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、5. 如图,OO的弦AB=8,M是AB的中点,且OM=3,则OO的半径等于( ) A、2 B、5 C、8 D、106. 如图, 是等腰直角三角形, 是斜边,将 绕点 逆时针旋转后,能与 重合,如果 ,那么 的长等于( )
A、2 B、5 C、8 D、106. 如图, 是等腰直角三角形, 是斜边,将 绕点 逆时针旋转后,能与 重合,如果 ,那么 的长等于( )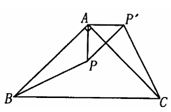 A、 B、 C、 D、7. 在Rt△ABC中,cosA= ,那么sinA的值是( )A、 B、 C、 D、8. 参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )A、 x(x+1)=110 B、 x(x﹣1)=110 C、x(x+1)=110 D、x(x﹣1)=1109. 如果关于x的一元二次方程 有两个实数根,那么 的取值范围是( )A、 B、 且 C、 且 D、10. 关于二次函数 ,下列说法正确的是( )A、图象的对称轴在 轴的右侧 B、图象与 轴的交点坐标为 C、图象与 轴的交点坐标为 和 D、 的最小值为-911. 某射击运动员在同一条件下的射击成绩记录如下:
A、 B、 C、 D、7. 在Rt△ABC中,cosA= ,那么sinA的值是( )A、 B、 C、 D、8. 参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛110场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )A、 x(x+1)=110 B、 x(x﹣1)=110 C、x(x+1)=110 D、x(x﹣1)=1109. 如果关于x的一元二次方程 有两个实数根,那么 的取值范围是( )A、 B、 且 C、 且 D、10. 关于二次函数 ,下列说法正确的是( )A、图象的对称轴在 轴的右侧 B、图象与 轴的交点坐标为 C、图象与 轴的交点坐标为 和 D、 的最小值为-911. 某射击运动员在同一条件下的射击成绩记录如下:射击次数
20
80
100
200
400
1000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A、0.90 B、0.82 C、0.85 D、0.8412. 有一题目:“已知;点 为 的外心, ,求 .”嘉嘉的解答为:画 以及它的外接圆 ,连接 , ,如图.由 ,得 .而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )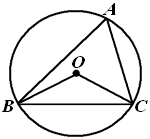 A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值13. 如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE( ,A,C,B三点共线),把一面镜子水平放置在平台上的点G处,测得 ,然后沿直线 后退到点E处,这时在镜子里恰好看到凉亭的顶端A,测得 .若小明身高1.6m,则凉亭的高度AB约为( )
A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值13. 如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE( ,A,C,B三点共线),把一面镜子水平放置在平台上的点G处,测得 ,然后沿直线 后退到点E处,这时在镜子里恰好看到凉亭的顶端A,测得 .若小明身高1.6m,则凉亭的高度AB约为( )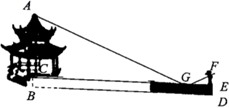 A、8.5m B、9m C、9.5m D、10m14. 臭豆腐是中国传统特色小吃,它“闻起来臭,吃起来香”.臭豆腐虽小,但制作流程却比较复杂.其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为: (a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A、8.5m B、9m C、9.5m D、10m14. 臭豆腐是中国传统特色小吃,它“闻起来臭,吃起来香”.臭豆腐虽小,但制作流程却比较复杂.其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为: (a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )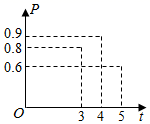 A、4.25分钟 B、4.05分钟 C、3.75分钟 D、2.75分钟
A、4.25分钟 B、4.05分钟 C、3.75分钟 D、2.75分钟二、填空题
-
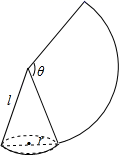
15. 计算: +( )﹣2﹣3tan60°+(π )0= .16. 将抛物线 的图象,向左平移1个单位,再向下平移2个单位,所得图象的解析式为 .17. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,则该圆锥的母线长 为cm.
 18. 如图, 三个顶点的坐标分别为 ,以点 为位似中心,相似比为 ,将 缩小,则点 的对应点 的坐标是 .
18. 如图, 三个顶点的坐标分别为 ,以点 为位似中心,相似比为 ,将 缩小,则点 的对应点 的坐标是 .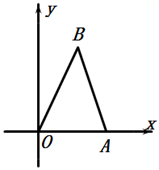 19. 对于实数a,b,定义运算“ ”, 例如 ,因为 ,所以 .若 是一元二次方程 的两个根,则 .
19. 对于实数a,b,定义运算“ ”, 例如 ,因为 ,所以 .若 是一元二次方程 的两个根,则 .三、解答题
-
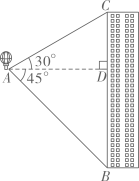
20. 现有4张正面分别写有数字1、2、3、4的卡片,将4张卡片的背面朝上,洗匀.(1)、若从中任意抽取1张,抽的卡片上的数字恰好为3的概率是;(2)、若先从中任意抽取1张(不放回),再从余下的3张中任意抽取1张,求抽得的2张卡片上的数字之和为3的倍数的概率.(请用“画树状图”或“列表”等方法写出分析过程)21. 热气球的探测器显示,从热气球A处看大楼BC顶部C的仰角为30°,看大楼底部B的俯角为45°,热气球与该楼的水平距离AD为60米,求大楼BC的高度.(结果精确到1米,参考数据: )
 22. 已知:如图在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.求证:△BEC∽△BCH.
22. 已知:如图在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.求证:△BEC∽△BCH.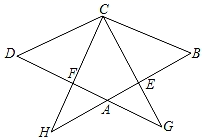 23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆,据统计,9月进馆120人次,进馆人次逐月增加,到11月末累计进馆570人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过450人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳12月的进馆人次,并说明理由.
23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆,据统计,9月进馆120人次,进馆人次逐月增加,到11月末累计进馆570人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过450人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳12月的进馆人次,并说明理由.