山东省临沂市河东区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 2cos45°的值等于( )A、1 B、 C、 D、22. 下列立体图形中,左视图与主视图不同的是( )A、
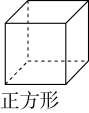 B、
B、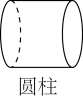 C、
C、 D、
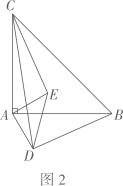
D、 3. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、4. 已知反比例函数 ,下列结论错误的是( )A、图象经过点(﹣2,1) B、图象在第二、四象限 C、当x<0时,y随着x的增大而增大 D、当x>﹣1时,y>25. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为( )
3. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、4. 已知反比例函数 ,下列结论错误的是( )A、图象经过点(﹣2,1) B、图象在第二、四象限 C、当x<0时,y随着x的增大而增大 D、当x>﹣1时,y>25. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为( )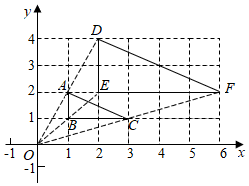 A、 B、2 C、4 D、26. 如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A、 B、2 C、4 D、26. 如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )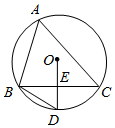 A、55° B、65° C、60° D、75°7. 已知点 , , 都在反比例函数 的图像上,且 ,则 , , 的大小关系是( )A、 B、 C、 D、8. 竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为( )A、 B、 C、 D、9. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )
A、55° B、65° C、60° D、75°7. 已知点 , , 都在反比例函数 的图像上,且 ,则 , , 的大小关系是( )A、 B、 C、 D、8. 竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为( )A、 B、 C、 D、9. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )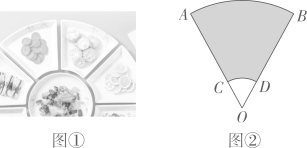 A、 B、 C、 D、10. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
A、 B、 C、 D、10. 如图, 中, ,点D在 上, .若 ,则 的长度为( )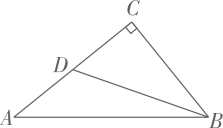 A、 B、 C、 D、411. 如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
A、 B、 C、 D、411. 如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
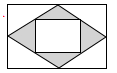 A、 B、 C、 D、12. 如图,函数 与函数 的图象相交于点 .若 ,则x的取值范围是( )
A、 B、 C、 D、12. 如图,函数 与函数 的图象相交于点 .若 ,则x的取值范围是( )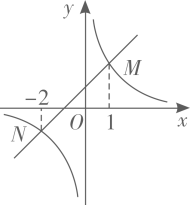 A、 或 B、 或 C、 或 D、 或13. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分 ,反比例函数 的图象经过AE上的两点A,F,且 , 的面积为18,则k的值为( )
A、 或 B、 或 C、 或 D、 或13. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分 ,反比例函数 的图象经过AE上的两点A,F,且 , 的面积为18,则k的值为( )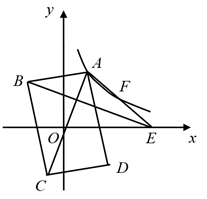 A、6 B、12 C、18 D、2414. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、6 B、12 C、18 D、2414. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )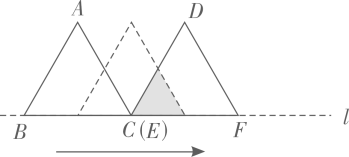 A、
A、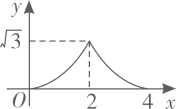 B、
B、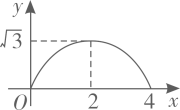 C、
C、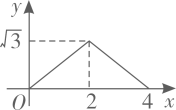 D、
D、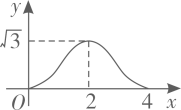
二、填空题
-
15. 已知关于 的一元二次方程 有实数根,则m的取值范围是 .16. 一个小球以 速度开始向前滚动,并且均匀减速, 后小球停止滚动.小球滚动 约用了秒(结果保留小数点后一位)17. 如图,在 中, , .将 绕点 按顺时针方向旋转至 的位置,点 恰好落在边 的中点处,则 的长为 .
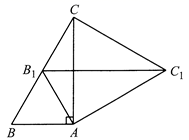 18. 如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为m.
18. 如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为m.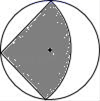 19. 如图,在 中, , ,若进行以下操作,在边 上从左到右依次取点 、 、 、 、…;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 …,则 .
19. 如图,在 中, , ,若进行以下操作,在边 上从左到右依次取点 、 、 、 、…;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 …,则 .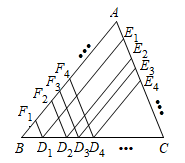
三、解答题
-
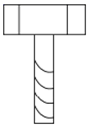
20.(1)、计算:4cos30°﹣3tan60°+2sin45°•cos45°(2)、解方程:x2+x﹣1=021. 随着“新冠肺炎”疫情防控形势日渐好转,各地开始复工复学,某校复学后成立“防疫志愿者服务队”,设立四个“服务监督岗”:①洗手监督岗,②戴口罩监督岗,③就餐监督岗,④操场活动监督岗.李老师和王老师报名参加了志愿者服务工作,学校将报名的志愿者随机分配到四个监督岗.(1)、李老师被分配到“洗手监督岗”的概率为(2)、用列表法或面树状图法,求李老师和王老师被分配到同一个监督岗的概率.22. 我们知道,机器上使用的螺丝钉(如图),它上面的螺纹以一定的角度旋转上升,使得螺钉旋转时向前推进,问直径是 的螺钉,若每转1圈向前推进 ,则螺纹的初始角约为多少度?(参考数据: , , , , , .)
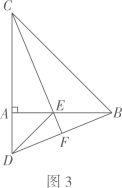
 23. 如图,点A,B,C是半径为2的⊙O上三个点,AB为直径,∠BAC的平分线交圆于点D,过点D作AC的垂线交AC得延长线于点E,延长线ED交AB得延长线于点F.
23. 如图,点A,B,C是半径为2的⊙O上三个点,AB为直径,∠BAC的平分线交圆于点D,过点D作AC的垂线交AC得延长线于点E,延长线ED交AB得延长线于点F.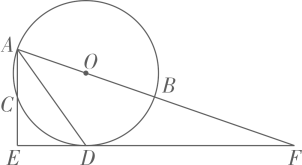 (1)、判断直线EF与⊙O的位置关系,并证明.(2)、若DF= ,求tan∠EAD的值.24. 如图,取一根长1米的匀质木杆,用细绳绑在木杆的中点 处并将其吊起来,在中点的左侧距离中点 处挂一个种9.8牛顿的物体,在中点右侧用一个弹簧秤向下拉,改变弹簧称与中点 的距离 (单位: ),看弹簧秤的示数 (单位:牛顿)有什么变化,小明在做此《数学活动》时,得到下表的数据:
(1)、判断直线EF与⊙O的位置关系,并证明.(2)、若DF= ,求tan∠EAD的值.24. 如图,取一根长1米的匀质木杆,用细绳绑在木杆的中点 处并将其吊起来,在中点的左侧距离中点 处挂一个种9.8牛顿的物体,在中点右侧用一个弹簧秤向下拉,改变弹簧称与中点 的距离 (单位: ),看弹簧秤的示数 (单位:牛顿)有什么变化,小明在做此《数学活动》时,得到下表的数据:1
10
15
20
25
30
35
40
45
/牛顿
125
24.5
16.5
12.3
9.8
8.2
7
■
5.4
结果老师发现其中有一个数据明显有不符合题意,另一个数据却被墨水涂黑了.
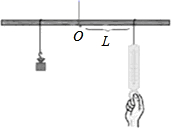 (1)、当 时的数据是错了;(2)、被墨水途黑了的数据你认为大概是;(3)、你能求出 与 的函数关系式吗?(4)、请你在直角坐标系中画出此函数的图象.
(1)、当 时的数据是错了;(2)、被墨水途黑了的数据你认为大概是;(3)、你能求出 与 的函数关系式吗?(4)、请你在直角坐标系中画出此函数的图象.