山东省聊城市莘县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 如图,在平行四边形 中,点 是边 上一点,且 , 交对角线 于点 ,则 与 的周长比为( )
 A、9 B、3 C、 D、22. 在 △ 中, , , ,则 的值为( )A、 B、 C、 D、3. 为防止疫情扩散,佩戴口罩成为疫情期间有效防范措施之一,某工厂为了能给市场提供充足的口罩,第一个月至第三个月生产口罩由67500袋增加到90000袋,设该工厂第一个月至第三个月生产口罩平均每月增长率为 ,则可列方程为( )A、 B、 C、 D、4. 如图,在⊙O中,直径AB⊥CD,∠A=26°,则∠D度数是( )
A、9 B、3 C、 D、22. 在 △ 中, , , ,则 的值为( )A、 B、 C、 D、3. 为防止疫情扩散,佩戴口罩成为疫情期间有效防范措施之一,某工厂为了能给市场提供充足的口罩,第一个月至第三个月生产口罩由67500袋增加到90000袋,设该工厂第一个月至第三个月生产口罩平均每月增长率为 ,则可列方程为( )A、 B、 C、 D、4. 如图,在⊙O中,直径AB⊥CD,∠A=26°,则∠D度数是( ) A、26° B、38° C、52° D、64°5. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、6. 在一个不透明的袋子中装有n个小球,这些球除颜色外均相同,其中红球有2个,如果从袋子中随机摸出一个球,这个球是红球的概率为 ,那么n的值是( )
A、26° B、38° C、52° D、64°5. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、6. 在一个不透明的袋子中装有n个小球,这些球除颜色外均相同,其中红球有2个,如果从袋子中随机摸出一个球,这个球是红球的概率为 ,那么n的值是( )
A、6 B、7 C、8 D、97. 将二次函数y=ax2的图象先向下平移2个单位,再向右平移3个单位,截x轴所得的线段长为4,则a=( )A、1 B、 C、 D、8. 菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:①BF为∠ABE的角平分线;②DF=2BF;③2AB2=DF•DB;④sin∠BAE= .其中正确的为( )
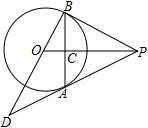
 A、①③ B、①②④ C、①④ D、①③④9. 如图,在半径为 的 中,弦 与 交于点E, , ,则CD的长是( )
A、①③ B、①②④ C、①④ D、①③④9. 如图,在半径为 的 中,弦 与 交于点E, , ,则CD的长是( )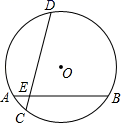 A、 B、 C、 D、10. 如图,在 中, 为 上一点,且 ,过点 作 于 ,连结 ,则 的值等于( )
A、 B、 C、 D、10. 如图,在 中, 为 上一点,且 ,过点 作 于 ,连结 ,则 的值等于( ) A、 B、2 C、 D、11. 如图,在平面直角坐标系中,将正方形 绕点O逆时针旋转 后得到正方形 ,依此方式,绕点O连续旋转 次得到正方 ,如果点A的坐标为 ,那么 的坐标为( )
A、 B、2 C、 D、11. 如图,在平面直角坐标系中,将正方形 绕点O逆时针旋转 后得到正方形 ,依此方式,绕点O连续旋转 次得到正方 ,如果点A的坐标为 ,那么 的坐标为( )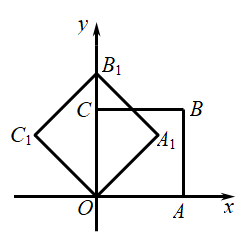 A、 B、 C、 D、12. 如图,抛物线 与x轴交于A、B两点与y轴交于点C.若点P是线段BC上方的抛物线上一动点,当 的面积取得最大值时,点P的坐标是( )
A、 B、 C、 D、12. 如图,抛物线 与x轴交于A、B两点与y轴交于点C.若点P是线段BC上方的抛物线上一动点,当 的面积取得最大值时,点P的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图, 内接于圆 , 是圆 的直径, ,则 的度数为 .
 14. 如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为 ,则 ( )的值为.
14. 如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为 ,则 ( )的值为.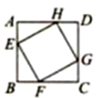 15. 如图,在平面直角坐标系中,点A是函数 (x<0)图象上的点,过点A作y轴的垂线交y轴于点B,点C在x轴上,若△ABC的面积为1,则k的值为 .
15. 如图,在平面直角坐标系中,点A是函数 (x<0)图象上的点,过点A作y轴的垂线交y轴于点B,点C在x轴上,若△ABC的面积为1,则k的值为 . 16. 如图,在扇形AOB中, ,半径OC交弦AB于点D,且 .若 ,则阴影部分的面积为 .
16. 如图,在扇形AOB中, ,半径OC交弦AB于点D,且 .若 ,则阴影部分的面积为 . 17. 有七张正面分别标有数字-3,-2,-1,0,l,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于 的一元二次方程 有两个不相等的实数根,且以x为自变量的二次函数 的图象不经过点(1,0)的概率是.
17. 有七张正面分别标有数字-3,-2,-1,0,l,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于 的一元二次方程 有两个不相等的实数根,且以x为自变量的二次函数 的图象不经过点(1,0)的概率是.三、解答题
-
18.(1)、计算: ;(2)、解方程:19. 如图,在平行四边形 中,过点 作 垂足为 ,连接 为线段 上一点,且 .
 (1)、求证: ;(2)、若 ,求 的长.20. “脱贫攻坚战”打响以来,全国贫困人口减少了8000多万人。某市为了扎实落实脱贫攻坚中“两不愁,三保障”的住房保障工作,2017年投入5亿元资金,之后投入资金逐年增长,2019年投入7.2亿元资金用于保障性住房建设.(1)、求该市这两年投入资金的年平均增长率.(2)、2020年该市计划保持相同的年平均增长率投入资金用于保障性住房建设,如果每户能得到保障房补助款3万元,则2020年该市能够帮助多少户建设保障性住房?21. 某地的一座人行天桥如图所示,天桥高为6米,坡面 的坡度为 ,文化墙 在天桥底部正前方8米处( 的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为 .(参考数据: , )
(1)、求证: ;(2)、若 ,求 的长.20. “脱贫攻坚战”打响以来,全国贫困人口减少了8000多万人。某市为了扎实落实脱贫攻坚中“两不愁,三保障”的住房保障工作,2017年投入5亿元资金,之后投入资金逐年增长,2019年投入7.2亿元资金用于保障性住房建设.(1)、求该市这两年投入资金的年平均增长率.(2)、2020年该市计划保持相同的年平均增长率投入资金用于保障性住房建设,如果每户能得到保障房补助款3万元,则2020年该市能够帮助多少户建设保障性住房?21. 某地的一座人行天桥如图所示,天桥高为6米,坡面 的坡度为 ,文化墙 在天桥底部正前方8米处( 的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为 .(参考数据: , )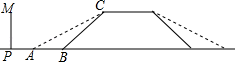 (1)、若新坡面坡角为 ,求坡角 度数;(2)、有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙 是否需要拆除?请说明理由.22. 某商店销售一种商品,每件进价为40元,对销售情况作了调查,结果发现月最大销售是 (件)与销售单价 (元) 之间的函数关系如图中的线段 .(月最大销售量指进货量足够的情况下最多售出件数)
(1)、若新坡面坡角为 ,求坡角 度数;(2)、有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙 是否需要拆除?请说明理由.22. 某商店销售一种商品,每件进价为40元,对销售情况作了调查,结果发现月最大销售是 (件)与销售单价 (元) 之间的函数关系如图中的线段 .(月最大销售量指进货量足够的情况下最多售出件数) (1)、求出 与 之间的函数表达式.(2)、该商品每月的总利润 (元),求 关于 的函数表达式,并指出销售单价 为多少元时利润 最大,该月进货数量应定为多少?(3)、若该商店进货350件,如果销售不完,就以亏本36元/件计入总利润,则销售单价定为多少,当月月利润最大?23. 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=
(1)、求出 与 之间的函数表达式.(2)、该商品每月的总利润 (元),求 关于 的函数表达式,并指出销售单价 为多少元时利润 最大,该月进货数量应定为多少?(3)、若该商店进货350件,如果销售不完,就以亏本36元/件计入总利润,则销售单价定为多少,当月月利润最大?23. 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y= 的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3. 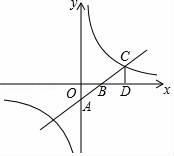 (1)、求一次函数与反比例函数的解析式;(2)、直接写出当x>0时,kx+b﹣
(1)、求一次函数与反比例函数的解析式;(2)、直接写出当x>0时,kx+b﹣ <0的解集.
<0的解集.