山东省聊城市临清市2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 30°角的正切值为( )A、 B、 C、 D、2. 如图,D为△ABC边BC上一点,要使△ABD∽△CBA,应该具备下列条件中的( )
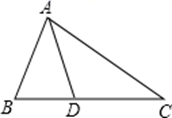 A、 B、 C、 D、3. 一元二次方程 配方后可化为( )A、 B、 C、 D、4. 将抛物线 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为:( )A、 B、 C、 D、5. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花,图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )
A、 B、 C、 D、3. 一元二次方程 配方后可化为( )A、 B、 C、 D、4. 将抛物线 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为:( )A、 B、 C、 D、5. 中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花,图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到 , , 两点之间的距离为 ,圆心角为 ,则图中摆盘的面积是( )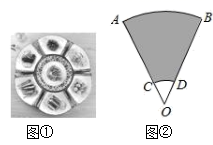 A、 B、 C、 D、6. 方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为( )A、12 B、15 C、12或15 D、不能确定7. 下列关于圆的说法中,正确的是( )A、等圆中,相等的弦所对的弧也相等 B、过圆心且平分弦的直线一定垂直于这条弦 C、经过半径的端点且垂直于这条半径的直线是圆的切线 D、三角形的内心一定在三角形内部,且到三条边的距离相等8. 如果P(m,y1),Q(﹣3,y2)在反比例函数 (k>0)的图象上,且y1>y2 , 则m的取值范围是( )A、m<﹣3 B、m>0或m<﹣3 C、﹣3<m<0 D、m>﹣39. 某小区2018年屋顶绿化面积为2000m2 , 计划2020年屋顶绿化面积要达到2880m2.设该小区2018年至2020年屋顶绿化面积的年平均增长率为x,则可列方程为( )A、2000(1+2x)=2880 B、2000×(1+x)=2880 C、2000+2000(1+x)+2000(1+x)2=2880 D、2000(1+x)2=288010. 如图,△ABC中,∠A=90°,AC=3,AB=4,半圆的圆心O在BC上,半圆与AB、AC分别相切于点D、E,则半圆的半径为( )
A、 B、 C、 D、6. 方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为( )A、12 B、15 C、12或15 D、不能确定7. 下列关于圆的说法中,正确的是( )A、等圆中,相等的弦所对的弧也相等 B、过圆心且平分弦的直线一定垂直于这条弦 C、经过半径的端点且垂直于这条半径的直线是圆的切线 D、三角形的内心一定在三角形内部,且到三条边的距离相等8. 如果P(m,y1),Q(﹣3,y2)在反比例函数 (k>0)的图象上,且y1>y2 , 则m的取值范围是( )A、m<﹣3 B、m>0或m<﹣3 C、﹣3<m<0 D、m>﹣39. 某小区2018年屋顶绿化面积为2000m2 , 计划2020年屋顶绿化面积要达到2880m2.设该小区2018年至2020年屋顶绿化面积的年平均增长率为x,则可列方程为( )A、2000(1+2x)=2880 B、2000×(1+x)=2880 C、2000+2000(1+x)+2000(1+x)2=2880 D、2000(1+x)2=288010. 如图,△ABC中,∠A=90°,AC=3,AB=4,半圆的圆心O在BC上,半圆与AB、AC分别相切于点D、E,则半圆的半径为( )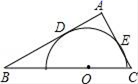 A、 B、 C、 D、11. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y 在同一平面直角坐标系中的图象可能是( )
A、 B、 C、 D、11. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b和反比例函数y 在同一平面直角坐标系中的图象可能是( )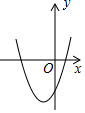 A、
A、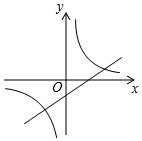 B、
B、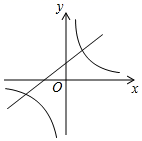 C、
C、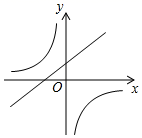 D、
D、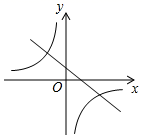 12. 春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过 的集中药物喷洒,再封闭宿舍 ,然后打开门窗进行通风,室内每立方米空气中含药量 与药物在空气中的持续时间 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
12. 春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过 的集中药物喷洒,再封闭宿舍 ,然后打开门窗进行通风,室内每立方米空气中含药量 与药物在空气中的持续时间 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )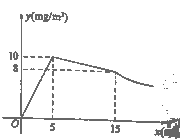 A、经过 集中喷洒药物,室内空气中的含药量最高达到 B、室内空气中的含药量不低于 的持续时间达到了 C、当室内空气中的含药量不低于 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效 D、当室内空气中的含药量低于 时,对人体才是安全的,所以从室内空气中的含药量达到 开始,需经过 后,学生才能进入室内
A、经过 集中喷洒药物,室内空气中的含药量最高达到 B、室内空气中的含药量不低于 的持续时间达到了 C、当室内空气中的含药量不低于 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效 D、当室内空气中的含药量低于 时,对人体才是安全的,所以从室内空气中的含药量达到 开始,需经过 后,学生才能进入室内二、填空题
-
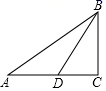
13. 正六边形的边长为2,则边心距为 .14. 如图,在Rt ABC中,∠C=90°,sinA= ,AB=10,D是AC的中点,则BD= .
 15. 如图,在 中, ,以 为直径作 ,分别交 、 于点E、F,则 弧的度数为°.
15. 如图,在 中, ,以 为直径作 ,分别交 、 于点E、F,则 弧的度数为°.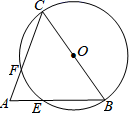 16. 某种服装平均每天可以销售20件,每件盈利32元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,若每天要盈利900元,每件应降价元.17. 如图,矩形ABCD的边长AB=3cm,AC=3 cm,动点M从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时动点N从点D出发,沿DA以2cm/s的速度向点A匀速运动.若△AMN与△ACD相似,则运动的时间t为s.
16. 某种服装平均每天可以销售20件,每件盈利32元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,若每天要盈利900元,每件应降价元.17. 如图,矩形ABCD的边长AB=3cm,AC=3 cm,动点M从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时动点N从点D出发,沿DA以2cm/s的速度向点A匀速运动.若△AMN与△ACD相似,则运动的时间t为s.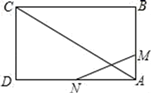
三、解答题
-
18. 解方程:(1)、 (用配方法);(2)、3x(x﹣1)=2(1﹣x);(3)、2x2+ x﹣5=0.19. 如图,在平行四边形ABCD中,点E在BC上,∠CDE=∠DAE.
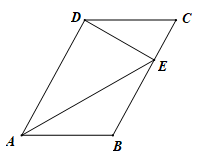 (1)、求证: ;(2)、若AD=6,DE=4,求CE的长.20. 如图,用长为24m.的篱笆,一面利用墙(墙的最大可用长度为10m)围成中间有一道篱笆的长方形花圃,现要围成面积为45 的花圃,求 的长是多少?
(1)、求证: ;(2)、若AD=6,DE=4,求CE的长.20. 如图,用长为24m.的篱笆,一面利用墙(墙的最大可用长度为10m)围成中间有一道篱笆的长方形花圃,现要围成面积为45 的花圃,求 的长是多少?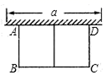 21. 如图,在斜坡PA的坡顶平台处有一座信号塔BC,在坡顶A处测得该塔的塔顶B的仰角为76°,在坡底的点P处测得塔顶B的仰角为45°,已知斜坡长PA=26m,坡度为1:2.4,点A与点C在同一水平面上,且AC PQ,BC⊥AC.请解答以下问题:
21. 如图,在斜坡PA的坡顶平台处有一座信号塔BC,在坡顶A处测得该塔的塔顶B的仰角为76°,在坡底的点P处测得塔顶B的仰角为45°,已知斜坡长PA=26m,坡度为1:2.4,点A与点C在同一水平面上,且AC PQ,BC⊥AC.请解答以下问题: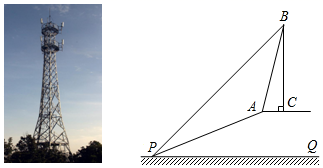 (1)、求坡顶A到地面PQ的距离;(2)、求信号塔BC的高度.(结果精确到1m,参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.00)22. 关于x的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、如果符合条件的最大整数k是一元二次方程 的根,求m的值.23. 如图,AB为⊙O的直径,C,D是⊙O上的点,P是⊙O外一点,AC⊥PD于点E,AD平分∠BAC.
(1)、求坡顶A到地面PQ的距离;(2)、求信号塔BC的高度.(结果精确到1m,参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.00)22. 关于x的一元二次方程 有两个不相等的实数根.(1)、求k的取值范围;(2)、如果符合条件的最大整数k是一元二次方程 的根,求m的值.23. 如图,AB为⊙O的直径,C,D是⊙O上的点,P是⊙O外一点,AC⊥PD于点E,AD平分∠BAC. (1)、求证:PD是⊙O的切线;(2)、若DE= ,∠BAC=60°,求⊙O的半径.24. 如图,直线y=mx+n与双曲线y= 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
(1)、求证:PD是⊙O的切线;(2)、若DE= ,∠BAC=60°,求⊙O的半径.24. 如图,直线y=mx+n与双曲线y= 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.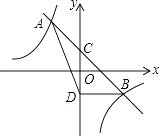 (1)、求m,n的值;(2)、若点D与点C关于x轴对称,求△ABD的面积;(3)、在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由.25. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且∠OBC=30°,OB=3OA.
(1)、求m,n的值;(2)、若点D与点C关于x轴对称,求△ABD的面积;(3)、在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由.25. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且∠OBC=30°,OB=3OA.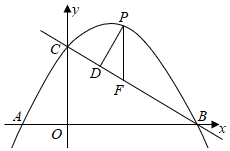 (1)、求抛物线y=ax2+bx+3的解析式;(2)、点P为直线BC上方抛物线上的一动点,P点横坐标为m,过点P作PF y轴交直线BC于点F,写出线段PF的长度l关于m的函数关系式;(3)、过点P作PD⊥BC于点D,当 PDF的周长最大时,求出 PDF周长的最大值及此时点P的坐标.
(1)、求抛物线y=ax2+bx+3的解析式;(2)、点P为直线BC上方抛物线上的一动点,P点横坐标为m,过点P作PF y轴交直线BC于点F,写出线段PF的长度l关于m的函数关系式;(3)、过点P作PD⊥BC于点D,当 PDF的周长最大时,求出 PDF周长的最大值及此时点P的坐标.