山东省聊城市茌平区2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下面关于x的方程中：①ax²＋bx＋c＝0；②3（x﹣9）²﹣（x＋1）²＝1；③x²＋ $\frac{1}{x}$ ＋5＝0；④x²＋5x³﹣6＝0；⑤3x²＝3（x﹣2）²；⑥12x﹣10＝0，是一元二次方程个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 下列关于事件发生可能性的表述，正确的是（）

A、“在地面向上抛石子后落在地上”是随机事件 B、掷两枚硬币，朝上面是一正面一反面的概率为 $\frac{1}{3}$ C、在同批次10000件产品中抽取100件发现有5件次品，则这批产品中大约有500件左右的次品 D、彩票的中奖率为10%，则买100张彩票必有10张中奖

查看试题解析
3. 在△ABC中，已知∠A、∠B均为锐角，且有|tan²B﹣3|＋（2sinA﹣ $\sqrt{3}$ ）²＝0，则△ABC是（）

A、等边三角形 B、直角三角形 C、等腰直角三角形 D、钝角三角形

查看试题解析
4. 如图，D是△ABC边AB上一点，添加一个条件后，仍然不能使△ACD∽△ABC的是（）

A、∠ACB＝∠ADC B、∠ACD＝∠ABC C、 $\frac{A C}{A B} = \frac{A D}{A C}$ D、 $\frac{C D}{B C} = \frac{A D}{A C}$

查看试题解析
5. 桌上摆着一个由若干个相同的小正方体组成的几何体，其主视图和左视图如图所示，则组成这个几何体的小正方体的个数最多有（）

A、12个 B、8个 C、14个 D、13个

查看试题解析
6. 一个三角形两边长分别为2和5，第三边长是方程x²－8x＋12＝0的根，则该三角形的周长为（）

A、9 B、11 C、13 D、9或13

查看试题解析
7. 若关于x的一元二次方程kx²﹣2x+ $\frac{1}{4}$ ＝0有两个实数根，则实数k的取值范围是（　　）

A、k＜4 B、k≤4 C、k＜4且k≠0 D、k≤4且k≠0

查看试题解析
8. 下列关于圆的叙述正确的有（）
①对角互补的四边形是圆内接四边形；②圆的切线垂直于圆的半径；③正多边形中心角的度数等于这个正多边形一个外角的度数；④过圆外一点所画的圆的两条切线长相等．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图， $∠ E F G = 90 ° ， E F = 10 ， O G = 17 ， \cos ∠ F G O = \frac{3}{5}$ ，则点 $F$ 的坐标是（）

A、 $(8 ， \frac{27}{4})$ B、 $(8 ， 12)$ C、 $(6 ， \frac{33}{4})$ D、 $(6 ， 10)$

查看试题解析
10. 如图，在用一坐标中，函数y＝ax²+bx（a≠0）与y＝ax+b的图象大致是（）

A、 B、 C、 D、

查看试题解析
11. 如图，在△ABC中，A，B两个顶点在x轴的上方，点C的坐标是（﹣1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形△A'B'C，使得△A'B'C的边长是△ABC的边长的2倍．设点B的横坐标是﹣3，则点B'的横坐标是（）

A、2 B、3 C、4 D、5

查看试题解析
12. 二次函数y＝ax²+bx+c的部分图象如图，图象过点A（3，0），对称轴为直线x＝1，下列结论：①a﹣b+c＝0；②2a+b＝0； ③4ac﹣b²＞0；④a+b≥am²+bm（m为实数）；⑤3a+c＞0．则其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 如图，随机地闭合开关S₁ ， S₂ ， S₃ ， S₄ ， S₅中的三个，能够使灯泡L₁ ， L₂同时发光的概率是．

查看试题解析
14. 抛物线y＝2（x﹣1）²＋c过（﹣2，y₁），（0，y₂），（ $\frac{5}{2}$ ，y₃）三点，则y₁ ， y₂ ， y₃大小关系是．

查看试题解析
15. 如图，在△ABC中，AD是BC上的高，且BC＝6，AD＝4，矩形EFGH的顶点F、G在边BC上，顶点E、H分别在边AB、AC上，设EF＝x（0＜x＜4），矩形EFGH的面积为y，那么y关于x的函数解析式为．

查看试题解析
16. 如图，设点P在函数y＝ $\frac{m}{x}$ 的图象上，PC⊥x轴于点C，交函数y＝ $\frac{n}{x}$ 的图象于点A，PD⊥y轴于点D，交函数y＝ $\frac{n}{x}$ 的图象于点B，若四边形PAOB的面积为8，则m﹣n＝．

查看试题解析
17. 在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为 $(1 ， 0)$ ，点D的坐标为 $(0 ， 2)$ ，延长CB交x轴于点 $A_{1}$ ，作正方形 $A_{1} B_{1} C_{1} C$ ，延长 $C_{1} B_{1}$ 交x轴于点 $A_{2}$ ，作正方形 $A_{2} B_{2} C_{2} C_{1} \dots$ 按这样的规律进行下去，第2020个正方形的面积为．

查看试题解析

三、解答题

18.

(1)、计算：|2﹣tan60°|﹣（π﹣3.14） ⁰＋ ${(- \frac{1}{2})}^{- 2}$ ＋ $\frac{1}{2} \sqrt{12}$ ．

(2)、解方程：2x（x﹣1）＝3（x﹣1）．

查看试题解析
19. 如图，在平面直角坐标系中， $△ O A B$ 的顶点坐标分别为 $O (0 ， 0)$ ， $A (2 ， 1)$ ， $B (1 ， - 2)$

⑴以原点O为位似中心，在y轴的右侧画出将 $△ O A B$ 放大为原来的2倍得到的 $△ O A_{1} B_{1}$ ，请写出点A的对应点 $A_{1}$ 的坐标；

⑵画出将 $△ O A B$ 向左平移2个单位，再向上平移1个单位后得到的 $△ O_{2} A_{2} B_{2}$ ，写出点B的对应点 $B_{2}$ 的坐标；

⑶请在图中标出 $△ O A_{1} B_{1}$ 与 $△ O_{2} A_{2} B_{2}$ 的位似中心M，并写出点M的坐标．

查看试题解析
20. 如图，在淮河的右岸边有一高楼，左岸边有一坡度 $i = 1 ： \sqrt{3}$ 的山坡 $C F$ ，点 $C$ 与点 $B$ 在同一水平面上， $C F$ 与 $A B$ 在同一平面内.某数学兴趣小组为了测量楼 $A B$ 的高度，在坡底 $C$ 处测得楼顶 $A$ 的仰角为 $45^{\circ}$ ，然后沿坡面 $C F$ 上行了 $10$ 米到达点 $D$ 处，此时在 $D$ 处测得楼顶 $A$ 的仰角为 $30^{\circ}$ ，求楼 $A B$ 的高度.（结果保留整数）（参考数 $\sqrt{3} \approx 1.7$ ）

查看试题解析
21. 如图，四边形ABCD内接于⊙O，对角线BD是⊙O的直径，AC平分∠BAD，过点C作CG∥BD交AD的延长线于点G．

(1)、求证：CG是⊙O的切线；

(2)、若AB＝3，AD＝5，求AC的长．

查看试题解析
22. 某学校为了增强学生体质，丰富课余生活，决定开设以下体育课外活动项目：A．篮球，B．乒乓球，C．羽毛球，D．足球．为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：

(1)、这次被调查的学生共有人，在扇形统计图中B区域的圆心角度数为；

(2)、请你将条形统计图补充完整；

(3)、在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，学校决定从这四名同学中任选两名参加市乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．

查看试题解析
23. 某厂为满足市场需求，改造了10条口罩生产线，每条生产线每天可生产口罩500个．如果每增加一条生产线，每条生产线每天就会少生产20个口罩．设增加x条生产线（x为正整数），每条生产线每天可生产口罩y个．

(1)、请直接写出y与x之间的函数关系式和自变量取值范围；

(2)、设该厂每天可以生产的口罩w个，请求出w与x的函数关系式，并求出当x为多少时，每天生产的口罩数量w最多？最多为多少个？

查看试题解析
24. 一次函数y₁＝kx＋b与反比例函数y₂＝ $\frac{m}{x}$ 的图象分别交于点B（2，4）和点C（n，2），与坐标轴分别交于点A和点D．

(1)、求一次函数的解析式；

(2)、根据图象直接写出不等式kx＋b＞ $\frac{m}{x}$ 的解；

(3)、若点P在x轴负半轴上，且sin∠BPD＝ $\frac{\sqrt{5}}{5}$ ，求点P的坐标．

查看试题解析
25. 如图，在平面直角坐标系中，已知抛物线 $y = x^{2} + b x + c$ 与直线 $A B$ 相交于A，B两点，其中 $A (1 ， 2)$ ， $B (﹣ 3 ， ﹣ 2)$ ．

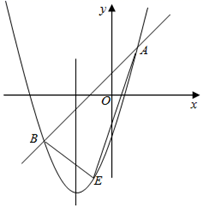(1)、求抛物线的函数表达式；

(2)、点E为直线 $A B$ 下方抛物线上任意一点，连接 $A E$ ， $B E$ ，求 $△ E A B$ 面积的最大值及此时点E的坐标；

(3)、点D为抛物线对称轴上的一点，当以点A，B，D为顶点的三角形为等腰三角形时，直接写出点D的坐标．

查看试题解析