山东省济宁市鱼台县2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中是反比例函数的是（）

A、 $y = - \frac{x}{2}$ B、 $y = x + 2$ C、 $y = - \frac{2}{x}$ D、 $y = \frac{2}{x} + 1$

查看试题解析
2. 下列各点在反比例函数 $y = - \frac{4}{x}$ 图像上的是（）

A、 $(1 ， 4)$ B、 $(- 2 ， 2)$ C、 $(- 2 ， - 2)$ D、 $(- 4 ， - 1)$

查看试题解析

3. 验光师测得一组关于近视眼镜的度数y（度）与镜片焦距x（米）的对应数据如下表．根据表中数据，可得y关于x的函数表达式为（）

近视眼镜的度数y（度）	200	250	400	500	1000
镜片焦距x（米）	0.50	0.40	0.25	0.20	0.10

A、

y = \frac{100}{x}

B、

y = \frac{x}{100}

C、

y = \frac{400}{x}

D、

y = \frac{x}{400}

查看试题解析

4. 如图，在 $△ A B C$ 中，若 $D E / / B C ， \frac{A D}{D B} = \frac{2}{3} ， D E = 4 c m$ ，则 $B C$ 的长是（）

A、 $7 c m$ B、 $10 c m$ C、 $13 c m$ D、 $15 c m$

查看试题解析
5. 如图，在⊙O中，弦AB为8mm，圆心O到AB的距离为3mm，则⊙O的半径等于（）

A、3mm B、4mm C、5mm D、8mm

查看试题解析
6. 如图，若 $A B$ 是 $⊙ О$ 的直径， $C D$ 是 $⊙ О$ 的弦， $∠ A B D = 55 ° ，$ 则 $∠ B C D$ 的度数为（）

A、 $35^{\circ}$ B、 $45^{\circ}$ C、 $55^{\circ}$ D、 $65^{\circ}$

查看试题解析
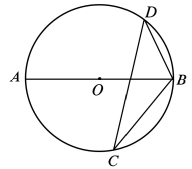7. 已知一次函数y=kx+b的图象如图，那么正比例函数y=kx和反比例函数y= $\frac{b}{x}$ 在同一坐标系中的图象的形状大致是（）

A、 B、 C、 D、

查看试题解析
8.
如图，下列条件不能判定△ADB∽△ABC的是（　　）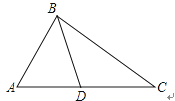

A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB²=AD•AC D、 $\frac{A D}{A B} = \frac{A B}{B C}$

查看试题解析
9. 有四张背面一模一样的卡片，卡片正面分别写着一个函数关系式，分别是 $y = 2 x ， y = x^{2} - 3 (x \geq 0) ， y = \frac{2}{x} (x > 0) ， y = - \frac{1}{3 x} (x < 0)$ ，将卡片顺序打乱后，随意从中抽取一张，取出的卡片上的函数是 $y$ 随 $x$ 的增大而增大的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
10. 用图中两个可自由转动的转盘做“配紫色”游戏；分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，那么可配成紫色的概率是（）

A、 $\frac{3}{12}$ B、 $\frac{5}{12}$ C、 $\frac{3}{8}$ D、 $\frac{5}{8}$

查看试题解析

二、填空题

11. 在﹣2，1，4，﹣3，0这5个数字中，任取一个数是负数的概率是．

查看试题解析
12. 已知反比例函数y＝ $\frac{k}{x}$ 过点（﹣2， $\frac{1}{2}$ ），则k＝．

查看试题解析
13. 已知： $y = (m - 2) x^{m^{2} - 5}$ 是反比例函数，则m= ．

查看试题解析
14. 反比例函数 $y = \frac{m + 2}{x}$ 的图象在每一象限，函数值 $y$ 都随 $x$ 增大而减小，那么 $m$ 的取值范围是．

查看试题解析
15. 点A $(- 2, y_{1})$ ，B $(- 1, y_{2})$ 都在反比例函数 $y = - \frac{3}{x}$ 图象上，则 $y_{1}$ $y_{2}$ .（填写<，>，=号）

查看试题解析

三、解答题

16. 若 $\frac{a + 2}{3} = \frac{b}{4} = \frac{c + 5}{6}$ ，且2a－b＋3c＝21.试求a∶b∶c.

查看试题解析
17. 如图，已知 $Δ A B C$ ，作 $⊙ O$ ，使它经过点 $A 、 B 、 C$ (保留作图痕迹，写出作法)．

查看试题解析
18. 不透明袋子中装有红、绿小球各一个，除颜色外无其他差别，随机摸出一个小球后，放回并摇匀，再随机摸出一个，求下列事件的概率．

(1)、两次都摸到红球；

(2)、第一次摸到红球，第二次摸到绿球．

查看试题解析
19. 一次函数y=kx+b的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于A(2，1) ，B(-1，n)两点．

(1)、求反比例函数的解析式；

(2)、求一次函数的解析式．

查看试题解析
20. 已知：如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于D，E为直角边AC的中点，过D，E作直线交AB的延长线于F.求证： $\frac{A B}{A C}$ ＝ $\frac{D F}{A F}$ .

查看试题解析
21. 某汽车销售商推出分期付款购车促销活动，交首付款后，余额要在30个月内结清，不计算利息，王先生在活动期间购买了价格为12万元的汽车，交了首付款后平均每月付款 $y$ 万元， $x$ 个月结清. $y$ 与 $x$ 的函数关系如图所示，根据图像回答下列问题：

(1)、确定 $y$ 与 $x$ 的函数解析式，并求出首付款的数目；

(2)、王先生若用20个月结清，平均每月应付多少万元？

(3)、如果打算每月付款不超过4000元，王先生至少要几个月才能结清余额？

查看试题解析
22. 如图， $A$ 是半径为 $12 cm$ 的 $⊙ O$ 上的定点，动点 $P$ 从 $A$ 出发，以 $2 πcm / s$ 的速度沿圆周逆时针运动，当点 $P$ 回到 $A$ 地立即停止运动．

(1)、如果 $∠ P O A = 90^{\circ}$ ，求点 $P$ 运动的时间；

(2)、如果点B是 $O A$ 延长线上的一点， $A B = O A$ ，那么当点 $P$ 运动的时间为 $2 s$ 时，判断直线BP与 $⊙ O$ 的位置关系，并说明理由．

查看试题解析
23. $⊙ О$ 直径 $A B = 12 c m ， A M$ 和 $B N$ 是 $⊙ О$ 的切线， $D C$ 切 $⊙ О$ 于点 $E$ 且交 $A M$ 于点 $D ，$ 交 $B N$ 于点 $C$ ，设 $A D = x ， B C = y$ ．

(1)、求 $y$ 与 $x$ 之间的关系式；

(2)、 $x ， y$ 是关于 $t$ 的一元二次方程 $2 t^{2} - 30 t + m = 0$ 的两个根，求 $x ， y$ 的值；

(3)、在（2）的条件下，求 $Δ C O D$ 的面积．

查看试题解析