山东省济宁市兖州区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 下列事件中,是必然事件的是( )A、掷一枚质地均匀的硬币,正面向上 B、任意买一张电影票,座位号是3的倍数 C、从一个只有白球的盒子里摸出一个球是白球 D、汽车走过一个红绿灯路口时,前方正好是绿灯2. 身高为165cm的小冰在中午时影长为55cm,小雪此时在同一地点的影长为60cm,那么小雪的身高为( )A、185cm B、180cm C、170cm D、160cm3. 如图,在 中, , ,则 的度数为( )
 A、30° B、35° C、45° D、60°4. 方程 的解是( )A、 B、 C、 D、5. 抛物线 与x轴的一个交点坐标为 ,对称轴是直线 ,其部分图象如图所示,则此抛物线与x轴的另一个交点坐标是( )
A、30° B、35° C、45° D、60°4. 方程 的解是( )A、 B、 C、 D、5. 抛物线 与x轴的一个交点坐标为 ,对称轴是直线 ,其部分图象如图所示,则此抛物线与x轴的另一个交点坐标是( )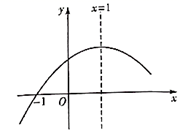 A、 B、 C、 D、6. 已知反比例函数 ,下列结论错误的是( )A、图象经过点(﹣2,1) B、图象在第二、四象限 C、当x<0时,y随着x的增大而增大 D、当x>﹣1时,y>27. 在 中, , , ,以C为圆心, cm长为半径的圆与AB的位置关系是( )A、相切 B、相交 C、相离 D、不能确定8. 如图,在5×5的网格中,每个小正方形的边长均为1,点A、B、O都在格点上.若将△OAB绕点O逆时针旋转90°,得到△OA′B′,A、B的对应点分别为A′、B′,则A、B′之间的距离为( )
A、 B、 C、 D、6. 已知反比例函数 ,下列结论错误的是( )A、图象经过点(﹣2,1) B、图象在第二、四象限 C、当x<0时,y随着x的增大而增大 D、当x>﹣1时,y>27. 在 中, , , ,以C为圆心, cm长为半径的圆与AB的位置关系是( )A、相切 B、相交 C、相离 D、不能确定8. 如图,在5×5的网格中,每个小正方形的边长均为1,点A、B、O都在格点上.若将△OAB绕点O逆时针旋转90°,得到△OA′B′,A、B的对应点分别为A′、B′,则A、B′之间的距离为( ) A、2 B、5 C、 D、9. 如图,一张矩形报纸ABCD的长AB=a,宽BC=b,E,F分别是AB,CD的中点,将这张报纸沿着直线EF对折后,矩形AEFD的长与宽的比等于矩形ABCD的长与宽的比,则a:b等于( )
A、2 B、5 C、 D、9. 如图,一张矩形报纸ABCD的长AB=a,宽BC=b,E,F分别是AB,CD的中点,将这张报纸沿着直线EF对折后,矩形AEFD的长与宽的比等于矩形ABCD的长与宽的比,则a:b等于( )
 A、 B、 C、 D、10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与y轴交于点B(0,﹣2),点A(﹣1,m)在抛物线上,则下列结论中错误的是( )
A、 B、 C、 D、10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与y轴交于点B(0,﹣2),点A(﹣1,m)在抛物线上,则下列结论中错误的是( )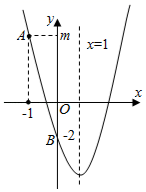 A、ab<0 B、一元二次方程ax2+bx+c=0的正实数根在2和3之间 C、a= D、点P1(t,y1),P2(t+1,y2)在抛物线上,当实数t> 时,y1<y2
A、ab<0 B、一元二次方程ax2+bx+c=0的正实数根在2和3之间 C、a= D、点P1(t,y1),P2(t+1,y2)在抛物线上,当实数t> 时,y1<y2二、填空题
-
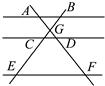
11. 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么 的值等于 .
 12. 一个不透明的袋中装有3个黑球和2个白球,这些球除颜色外都相同,从这个袋中任意摸出一个球为白球的概率是.13. 2019年12月6日,某市举行了2020年商品订货交流会,参加会议的每两家公司之间都签订了一份合同,所有参会公司共签订了28份合同,则共有家公司参加了这次会议.14. 如图,已知矩形OABC的面积为 ,它的对角线OB与双曲线 相交于点D,且OB:OD=5:3,则k=.
12. 一个不透明的袋中装有3个黑球和2个白球,这些球除颜色外都相同,从这个袋中任意摸出一个球为白球的概率是.13. 2019年12月6日,某市举行了2020年商品订货交流会,参加会议的每两家公司之间都签订了一份合同,所有参会公司共签订了28份合同,则共有家公司参加了这次会议.14. 如图,已知矩形OABC的面积为 ,它的对角线OB与双曲线 相交于点D,且OB:OD=5:3,则k=.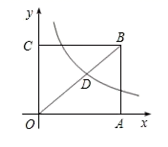 15. 如图,点 的坐标为 ,过点 作不轴的垂线交直 于点 以原点 为圆心, 的长为半径断弧交 轴正半轴于点 ;再过点 作 轴的垂线交直线 于点 ,以原点 为圆心,以 的长为半径画弧交 轴正半轴于点 ;…按此作法进行下去,则 的长是 .
15. 如图,点 的坐标为 ,过点 作不轴的垂线交直 于点 以原点 为圆心, 的长为半径断弧交 轴正半轴于点 ;再过点 作 轴的垂线交直线 于点 ,以原点 为圆心,以 的长为半径画弧交 轴正半轴于点 ;…按此作法进行下去,则 的长是 .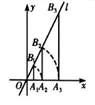 16. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长
16. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长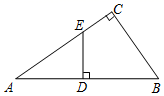
三、解答题
-
17. 已知关于 的一元二次方程 有两个不相等的实数根,(1)、求m的取值范围;(2)、当 时,求出此时方程的两个根.18. 奥体中心为满足暑期学生对运动的需求,欲开设球类课程,该中心随机抽取部分学生进行问卷调查,被调查学生须从“羽毛球”、“篮球”、“足球”、“排球”、“乒乓球”中选择自己最喜欢的一项.根据调查结果绘制了不完整的条形统计图和扇形统计图,请根据图中信息,解答下列问题:
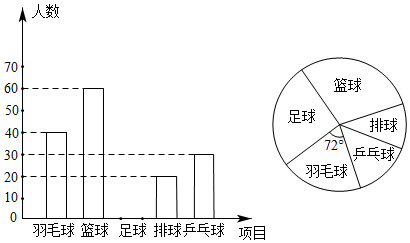 (1)、此次共调查了多少名学生?(2)、将条形统计图补充完整;(3)、我们把“羽毛球”“篮球”,“足球”、“排球”、“乒乓球”分别用A,B,C,D,E表示.小明和小亮分别从这些项目中任选一项进行训练,利用树状图或表格求出他俩选择不同项目的概率.19. 如图,在矩形ABCD中, , ,点P在BC边上运动,连接DP,过点A作 ,垂足为E.
(1)、此次共调查了多少名学生?(2)、将条形统计图补充完整;(3)、我们把“羽毛球”“篮球”,“足球”、“排球”、“乒乓球”分别用A,B,C,D,E表示.小明和小亮分别从这些项目中任选一项进行训练,利用树状图或表格求出他俩选择不同项目的概率.19. 如图,在矩形ABCD中, , ,点P在BC边上运动,连接DP,过点A作 ,垂足为E. (1)、设 , ,求y与x之间函数关系式;(2)、写出自变量x的取值范围,并求出y的最大值.20. 如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点.∠APC=∠CPB=60°.
(1)、设 , ,求y与x之间函数关系式;(2)、写出自变量x的取值范围,并求出y的最大值.20. 如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点.∠APC=∠CPB=60°.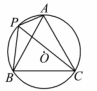 (1)、判断△ABC的形状:;(2)、试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)、当点P位于 的什么位置时,四边形APBC的面积最大?求出最大面积.21. 在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量 (单位:件)与线下售价 (单位:元/件, )满足一次函数的关系,部分数据如下表:
(1)、判断△ABC的形状:;(2)、试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)、当点P位于 的什么位置时,四边形APBC的面积最大?求出最大面积.21. 在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量 (单位:件)与线下售价 (单位:元/件, )满足一次函数的关系,部分数据如下表:x(元/件)
12
13
14
15
16
y(件)
1200
1100
1000
900
800
(1)、求 与 的函数关系式;(2)、若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.22. 定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角. (1)、如图1,∠E是△ABC中∠A的遥望角,若∠A=α,请用含α的代数式表示∠E.(2)、如图2,四边形ABCD内接于⊙O, = ,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)、如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.
(1)、如图1,∠E是△ABC中∠A的遥望角,若∠A=α,请用含α的代数式表示∠E.(2)、如图2,四边形ABCD内接于⊙O, = ,四边形ABCD的外角平分线DF交⊙O于点F,连结BF并延长交CD的延长线于点E.求证:∠BEC是△ABC中∠BAC的遥望角.(3)、如图3,在(2)的条件下,连结AE,AF,若AC是⊙O的直径.①求∠AED的度数;
②若AB=8,CD=5,求△DEF的面积.