山东省济宁市泗水县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 下列图形中,既是中心对称,又是轴对称的是( )A、
 B、
B、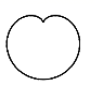 C、
C、 D、
D、 2. 已知 是方程 的一个实数根,则 的值是( )A、2016 B、2017 C、2018 D、20193. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
2. 已知 是方程 的一个实数根,则 的值是( )A、2016 B、2017 C、2018 D、20193. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ) A、
A、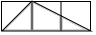 B、
B、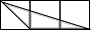 C、
C、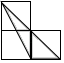 D、
D、 4. 已知点 ,它关于原点的对称点是点 ,则点 的坐标是( )A、(3,1) B、(1,-3) C、(-1,-3) D、(-3,-1)5. 已知点 , 是反比例函数 的图像上的两点,下列结论正确的是( )A、 B、 C、 D、6. 如图,边长为 的小正方形构成的网格中,半径为 的 的圆心 在格点上,则 的正切值为 ( )
4. 已知点 ,它关于原点的对称点是点 ,则点 的坐标是( )A、(3,1) B、(1,-3) C、(-1,-3) D、(-3,-1)5. 已知点 , 是反比例函数 的图像上的两点,下列结论正确的是( )A、 B、 C、 D、6. 如图,边长为 的小正方形构成的网格中,半径为 的 的圆心 在格点上,则 的正切值为 ( ) A、 B、 C、1 D、7. 如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y= (x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
A、 B、 C、1 D、7. 如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y= (x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( ) A、1 B、2 C、3 D、48. 如图, 、 分别为 的两条中线, 、 相交于点 ,连接 ,若 的面积为 ,则 的面积为( ).
A、1 B、2 C、3 D、48. 如图, 、 分别为 的两条中线, 、 相交于点 ,连接 ,若 的面积为 ,则 的面积为( ). A、2 B、 C、 D、19. 二次函数 的图象如图所示,则反比例函数 与一次函数 在同一坐标系内的大致图象是( )
A、2 B、 C、 D、19. 二次函数 的图象如图所示,则反比例函数 与一次函数 在同一坐标系内的大致图象是( ) A、
A、 B、
B、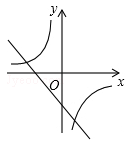 C、
C、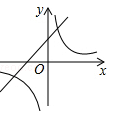 D、
D、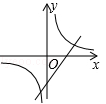 10. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )
10. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )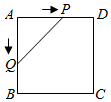 A、
A、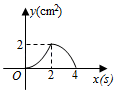 B、
B、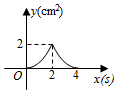 C、
C、 D、
D、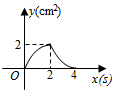
二、填空题
-
11. 将二次函数 化为 的形式,则 .12. 已知:∠A+∠B=90°,若sinA= ,则cosB=.13. 已知⊙O的直径为10cm,AB,CD是⊙O的两条弦, , , ,则 与 之间的距离为cm.14. 在物理课中,同学们曾学过小孔成像:在较暗的屋子里,把一只点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间放一块钻有小孔的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像,这种现象就是小孔成像(如图1).
如图2,如果火焰AB的高度是2cm,倒立的像A′B′的高度为5cm,蜡烛火焰根B到小孔O的距离为4cm,则火焰根的像B′到O的距离是cm.

 15. 如图,已知等边 ,顶点 在双曲线 上,点 的坐标为(2,0).过 作 ,交双曲线于点 ,过 作 交 轴于 ,得到第二个等边 .过 作 交双曲线于点 ,过 作 交 轴于点 得到第三个等边 ;以此类推,…,则点 的坐标为 , 的坐标为 .
15. 如图,已知等边 ,顶点 在双曲线 上,点 的坐标为(2,0).过 作 ,交双曲线于点 ,过 作 交 轴于 ,得到第二个等边 .过 作 交双曲线于点 ,过 作 交 轴于点 得到第三个等边 ;以此类推,…,则点 的坐标为 , 的坐标为 .
三、解答题
-
16. 解下列方程(1)、(2)、17. 在一个不透明的纸箱子中放有三张卡片,分别画有三个圆心角,其度数分别为 , , ,从纸箱中任意抽取一个圆心角,放回后再抽取第二个圆心角.求两次抽取的两个圆心角的正弦值组成的有序数对恰好在反比例函数 上的概率.(用列表或树状图解答)18. 如图,某轮船在海上向正东方向航行,在点 处测得小岛 在北偏东 方向,之后轮船继续向正东方向行驶 到达 处,这时小岛 在船的北偏东 方向 海里处.
 (1)、求轮船从 处到 处的航速.(2)、如果轮船按原速继续向正东方向航行,再经过多少时间轮船才恰好位于小岛 的东南方向?19. 如图,在 中, , 的平分线 交 于点 ,点 在 上,以 为直径的 经过点 .
(1)、求轮船从 处到 处的航速.(2)、如果轮船按原速继续向正东方向航行,再经过多少时间轮船才恰好位于小岛 的东南方向?19. 如图,在 中, , 的平分线 交 于点 ,点 在 上,以 为直径的 经过点 . (1)、求证:① 是 的切线;
(1)、求证:① 是 的切线;② ;
(2)、若点 是劣弧 的中点,且 ,试求阴影部分的面积.20. 某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:(1)、若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)、要使商场平均每天赢利最多,请你帮助设计方案.21. 我们知道:根据二次函数的图象,可以直接确定二次函数的最大(小)值;根据“两点之间,线段最短”,并运用轴对称的性质,可以在一条直线上找到一点,使得此点到这条直线同侧两定点之间的距离之和最短.这种数形结合的思想方法,非常有利于解决一些数学和实际问题中的最大(小)值问题.请你尝试解决一下问题: (1)、在图1中,抛物线所对应的二次函数的最大值是;(2)、在图2中,相距 的 、 两镇位于河岸(近似看做直线 )的同侧,且到河岸的距离 千米, 千米,现要在岸边建一座水塔,分别直接给两镇送水,为使所用水管的长度最短,请你:
(1)、在图1中,抛物线所对应的二次函数的最大值是;(2)、在图2中,相距 的 、 两镇位于河岸(近似看做直线 )的同侧,且到河岸的距离 千米, 千米,现要在岸边建一座水塔,分别直接给两镇送水,为使所用水管的长度最短,请你:
①作图确定水塔的位置;
②求出所需水管的长度.
(3)、已知 ,求 的最小值;此问题可以通过数形结合的方法加以解决,具体步骤如下:
①如图3中,作线段 ,分别过点 、 ,作 , ,使得 , ;
②在 上取一点 ,可设 , ; 的最小值即为线段和线段长度之和的最小值,最小值 .
 22. 如图所示,在平面直角坐标系中, 经过原点 ,且与 轴、 轴分别相交于 , 两点.
22. 如图所示,在平面直角坐标系中, 经过原点 ,且与 轴、 轴分别相交于 , 两点. (1)、请求出直线 的函数表达式;(2)、若有一抛物线的对称轴平行于 轴且经过点 ,顶点 在 上,开口向下,且经过点 ,求此抛物线的函数表达式;(3)、设 中的抛物线交 轴于 , 两点,在抛物线上是否存在点 ,使得 ?若存在,请求出点 的坐标;若不存在,请说明理由.
(1)、请求出直线 的函数表达式;(2)、若有一抛物线的对称轴平行于 轴且经过点 ,顶点 在 上,开口向下,且经过点 ,求此抛物线的函数表达式;(3)、设 中的抛物线交 轴于 , 两点,在抛物线上是否存在点 ,使得 ?若存在,请求出点 的坐标;若不存在,请说明理由.