山东省济宁市金乡县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 已知点P(2+m,n-3)与点Q(m,1+n)关于原点对称,则m-n的值是( )A、1 B、-1 C、2 D、-22. 下列美丽的壮锦图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 把二次函数y=x2﹣4x+3化成y=a(x﹣h)2+k的形式是( )A、y=(x﹣2)2﹣1 B、y=(x+2)2﹣1 C、y=(x﹣2)2+7 D、y=(x+2)2+74. 如图,从半径为5的⊙O外一点P引圆的两条切线PA , PB(A , B为切点),若∠APB=60°,则四边形OAPB的周长等于( )
3. 把二次函数y=x2﹣4x+3化成y=a(x﹣h)2+k的形式是( )A、y=(x﹣2)2﹣1 B、y=(x+2)2﹣1 C、y=(x﹣2)2+7 D、y=(x+2)2+74. 如图,从半径为5的⊙O外一点P引圆的两条切线PA , PB(A , B为切点),若∠APB=60°,则四边形OAPB的周长等于( )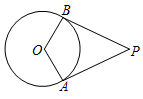 A、30 B、40 C、 D、5. 如图, 中, , , ,则 的长为( )
A、30 B、40 C、 D、5. 如图, 中, , , ,则 的长为( ) A、 B、 C、 D、6. 已知关于 的方程 的一个根为 ,则实数 的值为( )A、-1 B、1 C、-2 D、27. 若函数 的图象过点 ,则此函数图象位于( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限8. 下列说法错误的是( )A、必然事件发生的概率是1 B、通过大量重复试验,可以用频率估计概率 C、概率很小的事件不可能发生 D、投一枚图钉,“钉尖朝上”的概率不能用列举法求得9. 今年我市计划扩大城区绿地面积,现有一块长方形绿地,它的短边长为60m,若将短边增长到长边相等(长边不变),使扩大后的绿地的形状是正方形,则扩大后的绿地面积比原来增加1600 ,设扩大后的正方形绿地边长为xm,下面所列方程正确的是( )A、x(x-60)=1600 B、x(x+60)=1600 C、60(x+60)=1600 D、60(x-60)=160010. 对称轴为 的抛物线 如图所示,与 轴分别交于点 , , ,有下列五个结论:① ;② ;③ ( 为实数);④当 时, 随 增大而增大;⑤若方程 的两个实数根分别为 , ,且 ,则 , .其中错误结论的个数是( )
A、 B、 C、 D、6. 已知关于 的方程 的一个根为 ,则实数 的值为( )A、-1 B、1 C、-2 D、27. 若函数 的图象过点 ,则此函数图象位于( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限8. 下列说法错误的是( )A、必然事件发生的概率是1 B、通过大量重复试验,可以用频率估计概率 C、概率很小的事件不可能发生 D、投一枚图钉,“钉尖朝上”的概率不能用列举法求得9. 今年我市计划扩大城区绿地面积,现有一块长方形绿地,它的短边长为60m,若将短边增长到长边相等(长边不变),使扩大后的绿地的形状是正方形,则扩大后的绿地面积比原来增加1600 ,设扩大后的正方形绿地边长为xm,下面所列方程正确的是( )A、x(x-60)=1600 B、x(x+60)=1600 C、60(x+60)=1600 D、60(x-60)=160010. 对称轴为 的抛物线 如图所示,与 轴分别交于点 , , ,有下列五个结论:① ;② ;③ ( 为实数);④当 时, 随 增大而增大;⑤若方程 的两个实数根分别为 , ,且 ,则 , .其中错误结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是 .12. 如图,在 的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则 的值为 .
 13. 若 的弦 所对的圆心角为80°,则弦 所对的圆周角的度数是 .14. 如图所示,圆盘被分成8个全等的小扇形,分别写上数字1,2,3,4,5,6,7,8,自由转动圆盘,指针指向的数字 的概率是 .
13. 若 的弦 所对的圆心角为80°,则弦 所对的圆周角的度数是 .14. 如图所示,圆盘被分成8个全等的小扇形,分别写上数字1,2,3,4,5,6,7,8,自由转动圆盘,指针指向的数字 的概率是 . 15. 如图,矩形 的顶点 分别在 轴、 轴的正半轴上, 为 的中点,反比例函数 的图象经过点 ,且与 交于点 ,连接 , , ,若 的面积为3,则 的值为 .
15. 如图,矩形 的顶点 分别在 轴、 轴的正半轴上, 为 的中点,反比例函数 的图象经过点 ,且与 交于点 ,连接 , , ,若 的面积为3,则 的值为 .
三、解答题
-
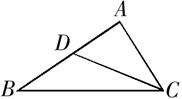
16.(1)、解方程 : ;(2)、已知: , ,求 的值.17. 如图,在△ABC中,点D在AB边上,∠ABC=∠ACD,
 (1)、求证:△ABC∽△ACD(2)、若AD=2,AB=5.求AC的长.18. 文化是一个国家,一个民族的灵魂,近年来,央视推出《中国诗词大会》《中国成语大会》《朗读者》《经典咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生须从《经典咏流传》(记为 )、《中国诗词大会》(记为 )、《中国成语大会》(记为 )、《朗读者》(记为 )中选择自己喜爱的一个栏目,也可以写出一个自己喜爱的其他文化栏目(记为 ).(1)、学生会随机抽查了一名学生,请问该生选择 的概率为多少?(2)、若选择 的学生中有2名女生,4名男生,现从选择 的学生中随机选出两名学生参加座谈,请用列表或画树状图的方法求出刚好选到同性别学生的概率.19. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C .
(1)、求证:△ABC∽△ACD(2)、若AD=2,AB=5.求AC的长.18. 文化是一个国家,一个民族的灵魂,近年来,央视推出《中国诗词大会》《中国成语大会》《朗读者》《经典咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生须从《经典咏流传》(记为 )、《中国诗词大会》(记为 )、《中国成语大会》(记为 )、《朗读者》(记为 )中选择自己喜爱的一个栏目,也可以写出一个自己喜爱的其他文化栏目(记为 ).(1)、学生会随机抽查了一名学生,请问该生选择 的概率为多少?(2)、若选择 的学生中有2名女生,4名男生,现从选择 的学生中随机选出两名学生参加座谈,请用列表或画树状图的方法求出刚好选到同性别学生的概率.19. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C .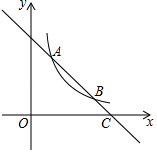 (1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.20. 如图,△ABC的顶点坐标分别为A(0,1),B(3,3) ,C(1,3) .
(1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.20. 如图,△ABC的顶点坐标分别为A(0,1),B(3,3) ,C(1,3) .
⑴画出△ABC关于点O的中心对称图形△A1B1C1;
⑵画出△ABC绕点A逆时针旋转90 的△AB2C2;直接写出点C2的坐标为 ▲ ;
⑶求在△ABC旋转到△AB2C2的过程中,点C所经过的路径长.
21. 阅读以下材料,并按要求完成相应地任务:

莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则 .
如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切分于点F,设⊙O的半径为R,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.
下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI,
∴ ,
∴ ①,
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF,
∵DE是⊙O的直径,∴∠DBE=90°,
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA,
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB,
∴ ,∴ ②,
任务:
(1)、观察发现: , (用含R,d的代数式表示);(2)、请判断BD和ID的数量关系,并说明理由;(3)、请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;(4)、应用:若△ABC的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为cm.22. 如图,已知抛物线 与 轴交于 、 两点, ,交 轴于点 ,对称轴是直线 . (1)、求抛物线的解析式及点 的坐标;(2)、连接 , 是线段 上一点, 关于直线 的对称点 正好落在 上,求点 的坐标;(3)、动点 从点 出发,以每秒2个单位长度的速度向点 运动,过 作 轴的垂线交抛物线于点 ,交线段 于点 .设运动时间为 秒.
(1)、求抛物线的解析式及点 的坐标;(2)、连接 , 是线段 上一点, 关于直线 的对称点 正好落在 上,求点 的坐标;(3)、动点 从点 出发,以每秒2个单位长度的速度向点 运动,过 作 轴的垂线交抛物线于点 ,交线段 于点 .设运动时间为 秒.①若 与 相似,请直接写出 的值;
② 能否为等腰三角形?若能,求出 的值;若不能,请说明理由.