山东省济南市天桥区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 下列四个几何体中,左视图为圆的是( )A、
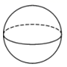 B、
B、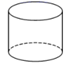 C、
C、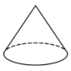 D、
D、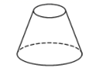 2. 已知反比例函数 的图象经过点P(3,2),则下列各点在这个函数图象上的是( )A、(-3,-2) B、(3,-2) C、(2,-3) D、(-2,3)3. 不透明布袋中装有除颜色外完全相同的1个红球和2个白球,搅匀后从中摸出一个球是白球的概率是( )A、 B、 C、 D、4. 下列结论中,菱形具有而矩形不一定具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对边相等且平行5. 如图,点A,B,C是⊙O上点,且∠AOB=60°,则∠ACB等于( )
2. 已知反比例函数 的图象经过点P(3,2),则下列各点在这个函数图象上的是( )A、(-3,-2) B、(3,-2) C、(2,-3) D、(-2,3)3. 不透明布袋中装有除颜色外完全相同的1个红球和2个白球,搅匀后从中摸出一个球是白球的概率是( )A、 B、 C、 D、4. 下列结论中,菱形具有而矩形不一定具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对边相等且平行5. 如图,点A,B,C是⊙O上点,且∠AOB=60°,则∠ACB等于( )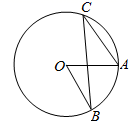 A、25° B、30° C、45° D、60°6. 如图,在△ABC中,∠A=90°,若AB=8,AC=6,则sinC的值为( )
A、25° B、30° C、45° D、60°6. 如图,在△ABC中,∠A=90°,若AB=8,AC=6,则sinC的值为( )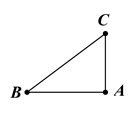 A、 B、 C、 D、7. 已知抛物线解析式为 ,则该抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线8. 如图,四边形ABCD为菱形,A , B两点的坐标分别是(2,0),(0,1),点C , D在坐标轴上,则菱形ABCD的周长等于( )
A、 B、 C、 D、7. 已知抛物线解析式为 ,则该抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线8. 如图,四边形ABCD为菱形,A , B两点的坐标分别是(2,0),(0,1),点C , D在坐标轴上,则菱形ABCD的周长等于( )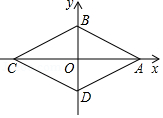 A、 B、4 C、4 D、209. 如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,BC=7m,则建筑物CD的高是( )
A、 B、4 C、4 D、209. 如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,BC=7m,则建筑物CD的高是( )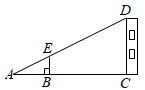 A、3.5m B、4m C、4.5m D、5m10. 原定于2020年10月在昆明举办的世界生物多样性大会第15次缔约方大会,因疫情推迟到2021年5月举办,为喜迎“COP15”,某校团委举办了以“COP15”为主题的学生绘画展览,为美化画面,要在长为30cm、宽为20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图),若设彩纸的宽度为xcm,根据题意可列方程( )
A、3.5m B、4m C、4.5m D、5m10. 原定于2020年10月在昆明举办的世界生物多样性大会第15次缔约方大会,因疫情推迟到2021年5月举办,为喜迎“COP15”,某校团委举办了以“COP15”为主题的学生绘画展览,为美化画面,要在长为30cm、宽为20cm的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等(如图),若设彩纸的宽度为xcm,根据题意可列方程( ) A、 B、 C、 D、11. 如图,点P为反比例函数 上的一个动点,作PD⊥x轴于点D,如果△POD的面积为m,则一次函数 的图象为( )
A、 B、 C、 D、11. 如图,点P为反比例函数 上的一个动点,作PD⊥x轴于点D,如果△POD的面积为m,则一次函数 的图象为( )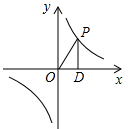 A、
A、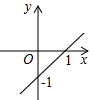 B、
B、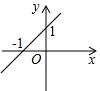 C、
C、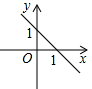 D、
D、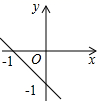 12. 已知二次函数 的图象如图所示,有以下结论:① ;② ;③ ;④ .正确结论的个数是( )
12. 已知二次函数 的图象如图所示,有以下结论:① ;② ;③ ;④ .正确结论的个数是( )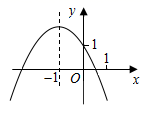 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
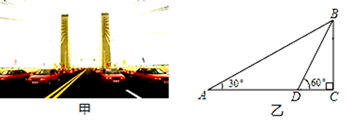
13. 一元二次方程 的解是.14. 圆内接正十边形中心角的度数为度.15. 若点(-2, )和( , )在函数 的图象上,则 (填“>”、“<”或“=”)16. 某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为米.(结果保留根号)
 17. 如图,在 中, 分别以 、 为直径画半圆,则图中阴影部分的面积为 . (结果保留 )
17. 如图,在 中, 分别以 、 为直径画半圆,则图中阴影部分的面积为 . (结果保留 )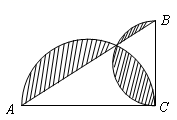 18. 如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF= .在以上4个结论中,其中一定成立的(把所有正确结论的序号都填在横线上)
18. 如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF= .在以上4个结论中,其中一定成立的(把所有正确结论的序号都填在横线上)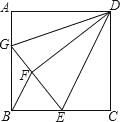
三、解答题
-
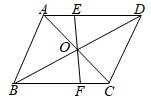
19. 计算:20. 解方程:21. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点E,F.求证:DE=BF.
 22. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
22. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好. (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)23. 如图,AB为⊙O的直径,C为⊙O上一点,AD⊥CE,垂足为D,AC平分∠DAB.
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)23. 如图,AB为⊙O的直径,C为⊙O上一点,AD⊥CE,垂足为D,AC平分∠DAB.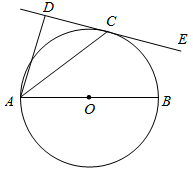 (1)、求证:CE是⊙O的切线;(2)、若AD=4, ,求AB的长.24. 某口罩生产厂生产的口罩1月份平均日产量为20000,1月底因突然爆发新冠肺炎疫情,市场对口罩需求量大增,为满足市场需求,工厂决定从2月份起扩大产能,3月份平均日产量达到24200个.(1)、求口罩日产量的月平均增长率;(2)、按照这个增长率,预计4月份平均日产量为多少?25. 如图,一次函数 与反比例函数 的图象相交于 两点,连接 ,延长 交反比例函数图象于点
(1)、求证:CE是⊙O的切线;(2)、若AD=4, ,求AB的长.24. 某口罩生产厂生产的口罩1月份平均日产量为20000,1月底因突然爆发新冠肺炎疫情,市场对口罩需求量大增,为满足市场需求,工厂决定从2月份起扩大产能,3月份平均日产量达到24200个.(1)、求口罩日产量的月平均增长率;(2)、按照这个增长率,预计4月份平均日产量为多少?25. 如图,一次函数 与反比例函数 的图象相交于 两点,连接 ,延长 交反比例函数图象于点 (1)、求一次函数 的表达式与反比例函数 的表达式;(2)、当 时,直接写出自变量 的取值范围为;(3)、点 是 轴上一点,当 时,请直接写出点 的坐标为 .26. 如图
(1)、求一次函数 的表达式与反比例函数 的表达式;(2)、当 时,直接写出自变量 的取值范围为;(3)、点 是 轴上一点,当 时,请直接写出点 的坐标为 .26. 如图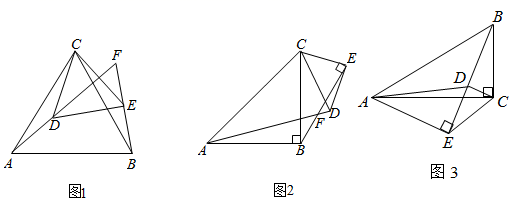 (1)、如图1,△ABC和△DEC均为等边三角形,直线AD和直线BE交于点F.
(1)、如图1,△ABC和△DEC均为等边三角形,直线AD和直线BE交于点F.填空:①请写出图1中的一对全等三角形:;
②线段AD,BE之间的数量关系为;
③∠AFB的度数为 .
(2)、如图2,△ABC和△DEC均为等腰直角三角形,∠ABC=∠DEC=90°,AB=BC,DE=EC,直线AD和直线BE交于点F.请判断∠AFB的度数及线段AD,BE之间的数量关系,并说明理由.(3)、如图3,△ABC和△ADE均为直角三角形,∠ACB=∠AED=90°,∠BAC=∠DAE=30°,AB=5,AE=3,当点B在线段ED的延长线上时,求线段BD和CE的长度.27. 如图,已知抛物线 过点C(0,2),交x轴于点A(-6, 0)和点B,抛物线的顶点为D,对称轴DE交x轴于点E,连接EC.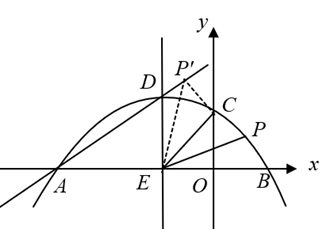 (1)、求抛物线的表达式;(2)、若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,直接写出点M坐标;(3)、点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.
(1)、求抛物线的表达式;(2)、若点M是抛物线对称轴DE上的点,当△MCE是等腰三角形时,直接写出点M坐标;(3)、点P是抛物线上的动点,连接PC,PE,将△PCE沿CE所在的直线对折,点P落在坐标平面内的点P′处.求当点P′恰好落在直线AD上时点P的横坐标.