山东省济南市商河县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
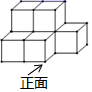
1. 如图所示的几何体,其俯视图是( )
 A、
A、 B、
B、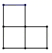 C、
C、 D、
D、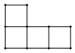 2. 方程 的根是( )A、 B、 C、 , D、 ,3. 菱形、矩形、正方形都具有的性质是( )A、对角线相等且互相平分 B、对角线相等且互相垂直 C、对角线互相平分 D、四条边相等4. 某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
2. 方程 的根是( )A、 B、 C、 , D、 ,3. 菱形、矩形、正方形都具有的性质是( )A、对角线相等且互相平分 B、对角线相等且互相垂直 C、对角线互相平分 D、四条边相等4. 某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( ) A、20 米 B、10米 C、10 米 D、20米5. 下列四个选项中的三角形,与图中的三角形相似的是( )
A、20 米 B、10米 C、10 米 D、20米5. 下列四个选项中的三角形,与图中的三角形相似的是( )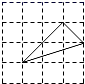 A、
A、 B、
B、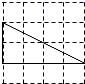 C、
C、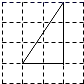 D、
D、 6. 函数 的图象与x轴有交点,则k的取值范围是( )A、 B、 且 C、 D、 且7. 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
6. 函数 的图象与x轴有交点,则k的取值范围是( )A、 B、 且 C、 D、 且7. 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果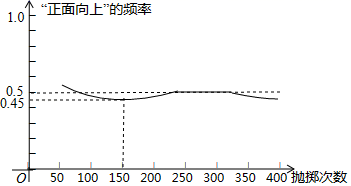
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A、① B、② C、①② D、①③8. 在同一平面直角坐标系中,函数 与 ( 为常数,且 )的图象大致( )A、 B、
B、 C、
C、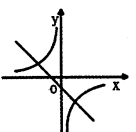 D、
D、 9. 电影《我和我的祖国》讲述了普通人与国家之间息息相关的动人故事.一上映就获得全国人民的追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若把平均每天票房的增长率记作x,则可以列方程为( )A、 B、 C、 D、10. 如图,已知双曲线 经过矩形 的边 的中点 ,交 于点 ,且四边形 的面积为2.则 ( )
9. 电影《我和我的祖国》讲述了普通人与国家之间息息相关的动人故事.一上映就获得全国人民的追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元,若把平均每天票房的增长率记作x,则可以列方程为( )A、 B、 C、 D、10. 如图,已知双曲线 经过矩形 的边 的中点 ,交 于点 ,且四边形 的面积为2.则 ( ) A、2 B、 C、1 D、411. 已知 中, ,点 是边 上一点(不与 、 重合),过 点的一条直线与 的边相交,所构成的三角形与原三角形相似,这样的直线有( )条
A、2 B、 C、1 D、411. 已知 中, ,点 是边 上一点(不与 、 重合),过 点的一条直线与 的边相交,所构成的三角形与原三角形相似,这样的直线有( )条 A、1 B、2 C、3 D、412. 将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )A、﹣ 或﹣12 B、﹣ 或2 C、﹣12或2 D、﹣ 或﹣12
A、1 B、2 C、3 D、412. 将二次函数y=x2﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象,若直线y=2x+b与这个新图象有3个公共点,则b的值为( )A、﹣ 或﹣12 B、﹣ 或2 C、﹣12或2 D、﹣ 或﹣12二、填空题
-
13. 如图,一人乘雪橇沿坡比1: 的斜坡笔直滑下72米,那么他下降的高度为米.
 14. 在一个不透明的袋子中放有a个球,其中有6个白球,这些球除颜色外完全相同,若每次把球充分搅匀后,任意摸出一一球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0.25左右,则a的值约为 .15. 如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2 , 则修建的路宽应为米.
14. 在一个不透明的袋子中放有a个球,其中有6个白球,这些球除颜色外完全相同,若每次把球充分搅匀后,任意摸出一一球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0.25左右,则a的值约为 .15. 如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2 , 则修建的路宽应为米. 16. 如图,二次函数 的图象与x轴交于 ,对称轴是直线 ,当函数值 时,自变量x的取值范围是 .
16. 如图,二次函数 的图象与x轴交于 ,对称轴是直线 ,当函数值 时,自变量x的取值范围是 . 17. 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y= (x>0)的图象经过A,B两点,若菱形ABCD的面积为2 ,则k的值为.
17. 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y= (x>0)的图象经过A,B两点,若菱形ABCD的面积为2 ,则k的值为. 18. 如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与点B,C重合),过点C作CN⊥DM交AB于点N,连结OM、ON,MN.下列五个结论:①△CNB≌△DMC;②ON=OM;③ON⊥OM;④若AB=2,则S△OMN的最小值是1;⑤AN2+CM2=MN2 . 其中正确结论是;(只填序号)
18. 如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与点B,C重合),过点C作CN⊥DM交AB于点N,连结OM、ON,MN.下列五个结论:①△CNB≌△DMC;②ON=OM;③ON⊥OM;④若AB=2,则S△OMN的最小值是1;⑤AN2+CM2=MN2 . 其中正确结论是;(只填序号)
三、解答题
-
19. 计算: +( )-2-3tan60°+(π- )020. 解方程:(1)、x2-2x-8=0(2)、x(x-3)=x-3.21. 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
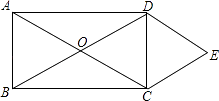
求证:四边形OCED是菱形.
22. 如图,连接A市和B市的高速公路是AC高速和BC高速,现在要修一条新高速AB,在施工过程中,决定在A、B两地开凿隧道,从而将两地间的公路进行改建,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶,已知BC=80千米,∠A=45°,∠B=30°. (1)、开通隧道前,汽车从A地到B地要走多少干来?(结果保留根号)(2)、开通隧道后,汽车从A地到B地少走多少千米?(结果保留根号)23. 某扶贫单位为了提高贫困户的经济收入,购买了33m的铁栅栏,准各用这些铁栅栏为贫困户靠墙(墙长15m)围建一个中间带有铁栅栏的矩形养鸡场(如图所示),
(1)、开通隧道前,汽车从A地到B地要走多少干来?(结果保留根号)(2)、开通隧道后,汽车从A地到B地少走多少千米?(结果保留根号)23. 某扶贫单位为了提高贫困户的经济收入,购买了33m的铁栅栏,准各用这些铁栅栏为贫困户靠墙(墙长15m)围建一个中间带有铁栅栏的矩形养鸡场(如图所示), (1)、若要建的矩形养鸡场面积为90m2 , 求鸡场的长(AB)和宽(BC);(2)、该扶贫单位想要建一个100m2的矩形养鸡场,这一想法能实现吗?请说明理由.24. 某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1、图2两幅均不完整的统计图表.
(1)、若要建的矩形养鸡场面积为90m2 , 求鸡场的长(AB)和宽(BC);(2)、该扶贫单位想要建一个100m2的矩形养鸡场,这一想法能实现吗?请说明理由.24. 某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1、图2两幅均不完整的统计图表.校本课程
频数
频率
A
36
0.45
B
0.25
C
16
b
D
8
合计
a
1

请您根据图表中提供的信息回答下列问题:
(1)、统计表中的a= , b=;(2)、“D”对应扇形的圆心角为度;(3)、根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;(4)、小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.25. 如图,在直角坐标系中,Rt 的直角边AC在x轴上,∠ACB=90°,AC=1,点B(3,2),反比例函数y= (k>0)的图象经过BC边的中点D. (1)、求这个反比例函数的表达式;(2)、若 与 成中心对称,且 的边FG在y轴的正半轴上,点E在这个函数的图象上,①求OF的长;②连接AF,BE,证明:四边形ABEF是正方形.26. 如图1,正方形ABCD和正方形AEFG,连接DG,BE
(1)、求这个反比例函数的表达式;(2)、若 与 成中心对称,且 的边FG在y轴的正半轴上,点E在这个函数的图象上,①求OF的长;②连接AF,BE,证明:四边形ABEF是正方形.26. 如图1,正方形ABCD和正方形AEFG,连接DG,BE (1)、[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是;位置关系是;(2)、[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;(3)、[应用]:在(2)情况下,连结GE(点E在AB上方),若GE//AB,且AB= ,AE=1,求线段DG的长27. 如图,抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,-3).
(1)、[发现]:当正方形AEFG绕点A旋转,如图2,线段DG与BE之间的数量关系是;位置关系是;(2)、[探究]:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,猜想DG与BE的数量关系与位置关系,并说明理由;(3)、[应用]:在(2)情况下,连结GE(点E在AB上方),若GE//AB,且AB= ,AE=1,求线段DG的长27. 如图,抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,-3).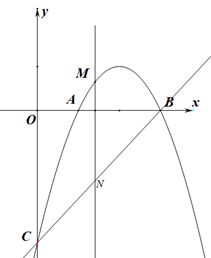 (1)、求抛物线的解析式;(2)、若点M是抛物线在x轴上方的部分上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值.(3)、在(2)的条件下,当MN取最大值时,在抛物线的对称轴上是否存在点P,使 是等腰三角形?若存在,请求出所有点P的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若点M是抛物线在x轴上方的部分上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值.(3)、在(2)的条件下,当MN取最大值时,在抛物线的对称轴上是否存在点P,使 是等腰三角形?若存在,请求出所有点P的坐标,若不存在,请说明理由.