山东省济南市莱芜区2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 下列函数中, 随 的增大而增大的函数有( )A、 B、 C、 D、2. 某种彩票的中奖机会是1%,下列说法正确的是( )A、买1张这种彩票一定不会中奖 B、买1张这种彩票一定会中奖 C、买100张这种彩票一定会中奖 D、当购买彩票的数量很大时,中奖的频率稳定在1%3. 如图所示的几何体,它的左视图是( )
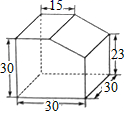 A、
A、 B、
B、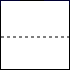 C、
C、 D、
D、 4. 如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B处仰角为30°,则甲楼高度为( )
4. 如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B处仰角为30°,则甲楼高度为( ) A、11米 B、(36﹣15 )米 C、15 米 D、(36﹣10 )米5. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )
A、11米 B、(36﹣15 )米 C、15 米 D、(36﹣10 )米5. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )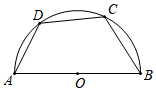 A、 B、 C、 D、6. 将抛物线y=ax2﹣1平移后与抛物线y=a(x﹣1)2重合,抛物线y=ax2﹣1上的点A(2,3)同时平移到A′,那么点A′的坐标为( )A、(3,4) B、(1,2) C、(3,2) D、(1,4)7. 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角45°的传送带AB,调整为坡度i=1: 的新传送带AC(如图所示).已知原传送带AB的长是4 米,那么新传送带AC的长是( )
A、 B、 C、 D、6. 将抛物线y=ax2﹣1平移后与抛物线y=a(x﹣1)2重合,抛物线y=ax2﹣1上的点A(2,3)同时平移到A′,那么点A′的坐标为( )A、(3,4) B、(1,2) C、(3,2) D、(1,4)7. 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角45°的传送带AB,调整为坡度i=1: 的新传送带AC(如图所示).已知原传送带AB的长是4 米,那么新传送带AC的长是( )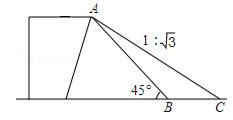 A、8米 B、4米 C、6米 D、3米8. 如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
A、8米 B、4米 C、6米 D、3米8. 如图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( ) A、5 B、 C、5 D、59. 如图,以 为直径,点 为圆心的半圆经过点 ,若 ,则图中阴影部分的面积为( )
A、5 B、 C、5 D、59. 如图,以 为直径,点 为圆心的半圆经过点 ,若 ,则图中阴影部分的面积为( ) A、 B、 C、 D、10. 工人师傅用一张半径为24cm,圆心角为150°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为( )cm.A、 B、 C、 D、11. 一次函数 与反比例函数 在同一坐标系中的图象可能是( )A、
A、 B、 C、 D、10. 工人师傅用一张半径为24cm,圆心角为150°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为( )cm.A、 B、 C、 D、11. 一次函数 与反比例函数 在同一坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 12. 在平面直角坐标系中,二次函数 的图象如图所示,现给出以下结论:
12. 在平面直角坐标系中,二次函数 的图象如图所示,现给出以下结论:
① ;② ;③ ;④ ( 为实数);⑤ .
其中正确结论的个数有( )
A、2 B、3 C、4 D、5二、填空题
-
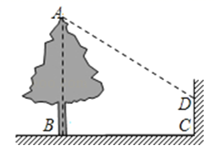
13. 如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于米.
 14. 二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx=0的根是 .15. 从 , , , 中任取两个不同的数,分别记为 和 ,则 的概率是 .16. 如图,矩形 的两边 的长分别为 , 是 的中点,反比例函数 的图象经过点 ,与 交于点 ,若 ,则 的值为 .
14. 二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx=0的根是 .15. 从 , , , 中任取两个不同的数,分别记为 和 ,则 的概率是 .16. 如图,矩形 的两边 的长分别为 , 是 的中点,反比例函数 的图象经过点 ,与 交于点 ,若 ,则 的值为 . 17. 如图,正六边形 的边长为 ,分别以点A, 为圆心,以 , 为半径作扇形 ,扇形 .则图中阴影部分的面积是 . (结果保留根号和 )
17. 如图,正六边形 的边长为 ,分别以点A, 为圆心,以 , 为半径作扇形 ,扇形 .则图中阴影部分的面积是 . (结果保留根号和 )
三、解答题
-
18. 计算: .19. 某小区为了促进生活垃圾的分类处理,将生活垃圾分为厨余、可回收和其他三类,分别记为 , , ,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱,分别记为 , , .若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率.20. 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
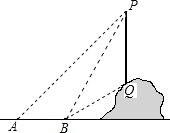 (1)、求∠BPQ的度数;(2)、求该电线杆PQ的高度(结果精确到1m).
(1)、求∠BPQ的度数;(2)、求该电线杆PQ的高度(结果精确到1m).备用数据: , .
21. 如图,已知反比例函数 与一次函数 交于点 和点 . (1)、求反比例函数和一次函数的表达式;(2)、求线段 的长;(3)、直接写出当 时 的取值范围.22. 某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.(1)、求w与x之间的函数关系式;(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少.
(1)、求反比例函数和一次函数的表达式;(2)、求线段 的长;(3)、直接写出当 时 的取值范围.22. 某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.(1)、求w与x之间的函数关系式;(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少.

