山东省菏泽市郓城县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 在菱形ABCD中,∠ABC=60゜,AC=4,则BD=( )
 A、 B、2 C、3 D、42. 定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤凰”方程.已知ax2+bx+c=0(a≠0)是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( )A、a=c B、a=b C、b=c D、a=b=c3. 某几何体的左视图如图所示,则该几何体不可能是( )
A、 B、2 C、3 D、42. 定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤凰”方程.已知ax2+bx+c=0(a≠0)是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( )A、a=c B、a=b C、b=c D、a=b=c3. 某几何体的左视图如图所示,则该几何体不可能是( )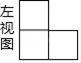 A、
A、 B、
B、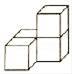 C、
C、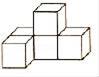 D、
D、 4. 对于函数 ,下列说法错误的是( )A、当x>0时,y的值随x的增大而增大 B、它的图象分布在第一、三象限,是轴对称图形 C、它的图象分布在第一、三象限,关于原点中心对称 D、当x<0时,y的值随x的增大而减小5. 面积为2的直角三角形一直角边长为x,另一直角边长为y,则y与x的变化规律用图象大致表示为( )A、
4. 对于函数 ,下列说法错误的是( )A、当x>0时,y的值随x的增大而增大 B、它的图象分布在第一、三象限,是轴对称图形 C、它的图象分布在第一、三象限,关于原点中心对称 D、当x<0时,y的值随x的增大而减小5. 面积为2的直角三角形一直角边长为x,另一直角边长为y,则y与x的变化规律用图象大致表示为( )A、 B、
B、 C、
C、 D、
D、 6. 如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了__米.(sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)( )
6. 如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了__米.(sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)( ) A、415 B、280 C、335 D、2507. 已知二次函数y=ax2+bx+c的x与y的部分对应值如下表:
A、415 B、280 C、335 D、2507. 已知二次函数y=ax2+bx+c的x与y的部分对应值如下表:x
-1
0
1
2
3
y
5
1
-1
-1
1
则该二次函数图象的对称轴为( )
A、y轴 B、直线x= C、直线x=2 D、直线x=8. 一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) A、
A、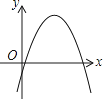 B、
B、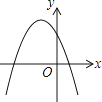 C、
C、 D、
D、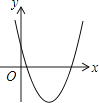
二、填空题
-
9. 在一个不透明的口袋中,装有若干个红球和6个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.3,则估计盒子中大约有红球。10. 如图,E为▱ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD= .
 11. 如图,三角尺在灯泡O的照射下在墙上形成影子,现测得OA=20cm,AA′═50cm,这个三角尺的周长与它在墙上形成影子的周长比是 .
11. 如图,三角尺在灯泡O的照射下在墙上形成影子,现测得OA=20cm,AA′═50cm,这个三角尺的周长与它在墙上形成影子的周长比是 . 12. 在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示.点P(4,3)在图象上,则当力达到10N时,物体在力的方向上移动的距离是m.
12. 在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示.点P(4,3)在图象上,则当力达到10N时,物体在力的方向上移动的距离是m. 13. 已知△ABC中,tanB= ,BC=6,过点A作BC边上的高,垂足为点D,且满足BD:CD=2:1,则△ABC面积为14. 如图,某公路隧道横截面为抛物线,其最大高度为8 m,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,若抛物线的表达式为y=- x2+b,则隧道底部宽AB为m.
13. 已知△ABC中,tanB= ,BC=6,过点A作BC边上的高,垂足为点D,且满足BD:CD=2:1,则△ABC面积为14. 如图,某公路隧道横截面为抛物线,其最大高度为8 m,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,若抛物线的表达式为y=- x2+b,则隧道底部宽AB为m.
三、解答题
-
15. 如图,在平行四边形ABCD中,E、F为BC上两点,且BE=CF,AF=DE,求证:
 (1)、△ABF≌△DCE;(2)、四边形ABCD是矩形.16. 已知关于x的方程x2+(2k﹣1)x+k2﹣1=0有两个实数根x1 , x2 .(1)、求实数k的取值范围;(2)、若x1 , x2满足x12+x22=16+x1x2 , 求实数k的值.17. 甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示. 游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转.
(1)、△ABF≌△DCE;(2)、四边形ABCD是矩形.16. 已知关于x的方程x2+(2k﹣1)x+k2﹣1=0有两个实数根x1 , x2 .(1)、求实数k的取值范围;(2)、若x1 , x2满足x12+x22=16+x1x2 , 求实数k的值.17. 甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示. 游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转. (1)、请用树状图或列表法列出所有可能的结果;(2)、若指针所指的两个数字都是方程x2-4x+3=0的解时,则甲获胜;若指针所指的两个数字都不是方程x2-4x+3=0的解时,则乙获胜.问他们两人谁获胜的概率大?请分析说明.18. 如图,在△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE∥AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD,AE.
(1)、请用树状图或列表法列出所有可能的结果;(2)、若指针所指的两个数字都是方程x2-4x+3=0的解时,则甲获胜;若指针所指的两个数字都不是方程x2-4x+3=0的解时,则乙获胜.问他们两人谁获胜的概率大?请分析说明.18. 如图,在△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE∥AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD,AE. (1)、求证:△ABC∽△BGA;(2)、若AF=5,AB=8,求FG的长;19. 如图是由一些棱长都为 的小正方体组合成的简单几何体.
(1)、求证:△ABC∽△BGA;(2)、若AF=5,AB=8,求FG的长;19. 如图是由一些棱长都为 的小正方体组合成的简单几何体. (1)、该几何体的表面积(含下底面)为 .(2)、该几何体的主视图如图所示,请按照主视图的阴影方式在下面的方格纸中分别画出它的左视图和俯视图.
(1)、该几何体的表面积(含下底面)为 .(2)、该几何体的主视图如图所示,请按照主视图的阴影方式在下面的方格纸中分别画出它的左视图和俯视图. 20. 在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.(1)、设矩形的相邻两边长分别为x,y.
20. 在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.(1)、设矩形的相邻两边长分别为x,y.①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)、圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?21. 如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:∠A=90°,∠ABD=60°,∠CBD=54°,AB=200 m,BC=300 m.请你计算出这片水田的面积.(参考数据:sin 54°≈0.809,cos 54°≈0.588,tan 54°≈1.376, =1.732) 22. 某网店销售某款童装,每件售价60元,每星期可卖300件.为了促销,该店决定降价销售,市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元.设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定多少元时,每星期的销售利润最大,最大利润是多少?
22. 某网店销售某款童装,每件售价60元,每星期可卖300件.为了促销,该店决定降价销售,市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元.设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定多少元时,每星期的销售利润最大,最大利润是多少?

