山东省菏泽市鄄城县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 一元二次方程 有实数根,则k的取值范围是( )A、 且 B、 C、 且 D、 或2. 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
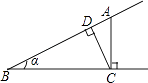 A、 B、 C、 D、3. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( )
A、 B、 C、 D、3. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( ) A、
A、 B、
B、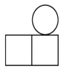 C、
C、 D、
D、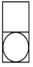 4. 在四张背面完全相同的卡片上分别印有正方形、正五边形、正六边形、圆的图案,现将印有图案的一面朝下,混合后从中随机抽取两张,则抽到卡片上印有的图案都是中心对称图形的概率为( )A、 B、 C、 D、5. 如图,点A在双曲线 上,点B在双曲线 上,且AB//x轴,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为( )
4. 在四张背面完全相同的卡片上分别印有正方形、正五边形、正六边形、圆的图案,现将印有图案的一面朝下,混合后从中随机抽取两张,则抽到卡片上印有的图案都是中心对称图形的概率为( )A、 B、 C、 D、5. 如图,点A在双曲线 上,点B在双曲线 上,且AB//x轴,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为( )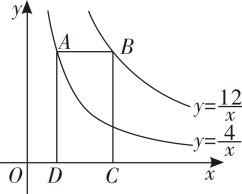 A、4 B、6 C、8 D、126. 如图,平行四边形 的对角线 , 相交于点O,E是 的中点,则 与 的面积的比等于( )
A、4 B、6 C、8 D、126. 如图,平行四边形 的对角线 , 相交于点O,E是 的中点,则 与 的面积的比等于( )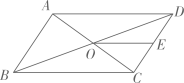 A、 B、 C、 D、7. 如图,抛物线 交x轴于点A,B,交 轴于点C.若点A坐标为 ,对称轴为直线 ,则下列结论错误的是( )
A、 B、 C、 D、7. 如图,抛物线 交x轴于点A,B,交 轴于点C.若点A坐标为 ,对称轴为直线 ,则下列结论错误的是( ) A、二次函数的最大值为 B、 C、 D、8. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点 处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( )
A、二次函数的最大值为 B、 C、 D、8. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点 处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
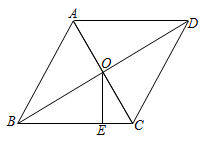
9. 计算:cos245°-tan30°sin60°= .10. 在一个不透明的袋子中装有6个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出白球的频率稳定在0.3附近,则估计袋子中的红球有个.11. 如图,菱形 的对角线 , 相交于点 ,过点 作 于点 ,若 , ,则 .
 12. 如图,在平面直角坐标系中,△ 与△ 是以原点O为位似中心的位似图形,且相似比为3:2.点 的坐标为(3, ),则点 的坐标是 .
12. 如图,在平面直角坐标系中,△ 与△ 是以原点O为位似中心的位似图形,且相似比为3:2.点 的坐标为(3, ),则点 的坐标是 .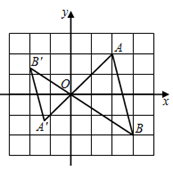 13. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图所示的是一个根据北京的地理位置设计的圭表,其中,立柱AC的高为a,已知冬至时北京的正午日光的入射角∠ABC为30°,则立柱根部与圭表的冬至线的距离即BC的长)为(用含a的代数式表示)
13. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图所示的是一个根据北京的地理位置设计的圭表,其中,立柱AC的高为a,已知冬至时北京的正午日光的入射角∠ABC为30°,则立柱根部与圭表的冬至线的距离即BC的长)为(用含a的代数式表示)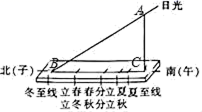 14. 如图,一段抛物线: 记为 ,它与 轴交于两点 , ;将 绕 旋转 得到 ,交 轴于 ;将 绕 旋转 得到 ,交 轴于 ; 如此进行下去,直至得到 ,若点 在第 段抛物线 上,则 .
14. 如图,一段抛物线: 记为 ,它与 轴交于两点 , ;将 绕 旋转 得到 ,交 轴于 ;将 绕 旋转 得到 ,交 轴于 ; 如此进行下去,直至得到 ,若点 在第 段抛物线 上,则 .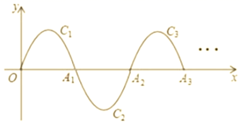
三、解答题
-
15. 用适当的方法求解下列方程:(1)、 ;(2)、 .16. 如图,路灯(P点)距地面9米,身高1.5米的小云从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
 17. 图1是某种路灯的实物图片,图2是该路灯的平面示意图, 为立柱的一部分,灯臂 ,支架 与立柱 分别交于A,B两点,灯臂 与支架 交于点C,已知 , , ,求支架 的长.(结果精确到 ,参考数据: , , )
17. 图1是某种路灯的实物图片,图2是该路灯的平面示意图, 为立柱的一部分,灯臂 ,支架 与立柱 分别交于A,B两点,灯臂 与支架 交于点C,已知 , , ,求支架 的长.(结果精确到 ,参考数据: , , )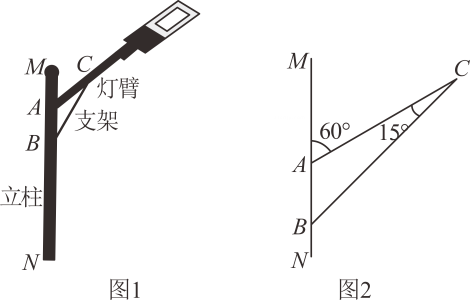 18. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
18. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.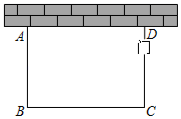 19. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.
19. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.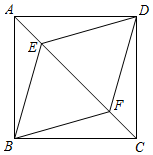 20. 如图,在矩形 中,E是 的中点, ,垂足为F.
20. 如图,在矩形 中,E是 的中点, ,垂足为F.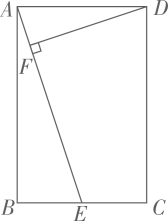 (1)、求证: ;(2)、若 , ,求 的长.21. “2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动.规则是:准备3张大小一样,背面完全相同的卡片,3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》,将它们背面朝上洗匀后任意抽出一张,抽到卡片后可以免费领取卡片上相应的书籍.(1)、在上面的活动中,如果从中随机抽出一张卡片,记下内容后不放回,再随机抽出一张卡片,请用列表或画树状图的方法,求恰好抽到2张卡片都是《辞海》的概率;(2)、再添加几张和原来一样的《消防知识手册》卡片,将所有卡片背面朝上洗匀后,任意抽出一张,使得抽到《消防知识手册》卡片的概率为 ,那么应添加多少张《消防知识手册》卡片?请说明理由.22. 如图,一次函数 的图象与反比例函数 的图象相交于 , 两点.
(1)、求证: ;(2)、若 , ,求 的长.21. “2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动.规则是:准备3张大小一样,背面完全相同的卡片,3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》,将它们背面朝上洗匀后任意抽出一张,抽到卡片后可以免费领取卡片上相应的书籍.(1)、在上面的活动中,如果从中随机抽出一张卡片,记下内容后不放回,再随机抽出一张卡片,请用列表或画树状图的方法,求恰好抽到2张卡片都是《辞海》的概率;(2)、再添加几张和原来一样的《消防知识手册》卡片,将所有卡片背面朝上洗匀后,任意抽出一张,使得抽到《消防知识手册》卡片的概率为 ,那么应添加多少张《消防知识手册》卡片?请说明理由.22. 如图,一次函数 的图象与反比例函数 的图象相交于 , 两点.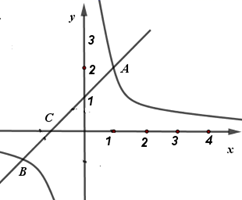 (1)、求一次函数和反比例函数的表达式;(2)、直线 交 轴于点 ,点 是 轴上的点,若 的面积是 ,求点 的坐标.23. 实践操作:第一步:如图1,将矩形纸片 沿过点D的直线折叠,使点A落在 上的点 处,得到折痕 ,然后把纸片展平.第二步:如图2,将图1中的矩形纸片 沿过点E的直线折叠,点C恰好落在 上的点 处,点B落在点 处,得到折痕 , 交 于点M, 交 于点N,再把纸片展平.
(1)、求一次函数和反比例函数的表达式;(2)、直线 交 轴于点 ,点 是 轴上的点,若 的面积是 ,求点 的坐标.23. 实践操作:第一步:如图1,将矩形纸片 沿过点D的直线折叠,使点A落在 上的点 处,得到折痕 ,然后把纸片展平.第二步:如图2,将图1中的矩形纸片 沿过点E的直线折叠,点C恰好落在 上的点 处,点B落在点 处,得到折痕 , 交 于点M, 交 于点N,再把纸片展平.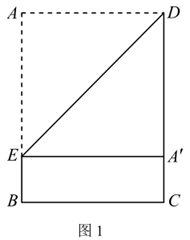
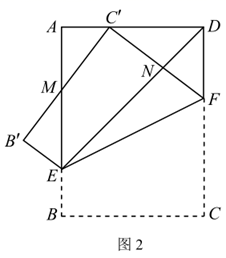
问题解决:
(1)、如图1,填空:四边形 的形状是;(2)、如图2,线段 与 是否相等?若相等,请给出证明;若不等,请说明理由;(3)、如图2,若 ,求 的值.24. 如图,二次函数 的图象交x轴于点 , ,交y轴于点C.点 是x轴上的一动点, 轴,交直线 于点M,交抛物线于点N. (1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;
(1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.