山东省东营市垦利区2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 反比例函数y＝ $\frac{k}{x}$ 的图象经过点A（﹣2，3），则此图象一定经过下列哪个点（）

A、（3，2） B、（﹣3，﹣2） C、（﹣3，2） D、（﹣2，﹣3）

查看试题解析
2. 在正面完全相同、反面印有下列四个图形的纸片中，任抽一张，则抽到的图形中，既是轴对称图形，又是中心对称图形的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
3. 如图，五边形ABCDE是⊙O的内接正五边形，则正五边形中心角∠COD的度数是（）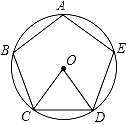

A、60° B、36° C、76° D、72°

查看试题解析
4. 关于抛物线 $y = - x^{2} + 2 x - 3$ ，下列说法正确的是（）

A、开口方向向上 B、顶点坐标为 $(1 ， - 2)$ C、与x轴有两个交点 D、对称轴是直线 $x = - 1$

查看试题解析
5. 在△ABC中，已知∠C=90°，BC=4，sinA= $\frac{2}{3}$ ，那么AC边的长是（）

A、6 B、2 $\sqrt{5}$ C、3 $\sqrt{5}$ D、2 $\sqrt{13}$

查看试题解析
6. 将抛物线y＝﹣2（x+2）²+5向右平移3个单位，再向下平移2个单位，所得抛物线解析式为（）

A、y＝﹣2（x+1）²+3 B、y＝﹣2（x+5）²+7 C、y＝﹣2（x﹣1）²+3 D、y＝﹣2（x﹣1）²+7

查看试题解析
7. 如图， $A B ， C E$ 均 $⊙ O$ 为直径，点 $C ， D$ 是圆上两点，且 $∠ C D B = 28^{°}$ ，则 $∠ E$ 的度数是（）

A、 $62^{°}$ B、 $56^{°}$ C、 $66^{°}$ D、 $76^{°}$

查看试题解析
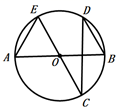8. 如图，反比例函数 $y = \frac{1}{x}$ 的图象与矩形ABCO的边AB、BC相交于E、F两点，点A、C在坐标轴上．若 $B E = 2 A E$ ，则四边形OEBF的面积为（）

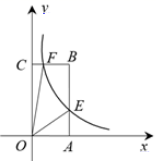A、1 B、2 C、3 D、4

查看试题解析
9. 一人一盔安全守规，一人一带平安常在！某商店销售一批头盔，售价为每顶80元，每月可售出200顶．在“创建文明城市”期间，计划将头盔降价销售，经调查发现：每降价1元，每月可多售出20顶．已知头盔的进价为每顶50元，则该商店每月获得最大利润时，每顶头盔的售价为（）元．

A、60 B、65 C、70 D、75

查看试题解析
10. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图所示，则下列结论中错误的有（）个．
①abc＞0；②2a+b＝0；③9a+3b+c＜0；④4ac﹣b²＜0；⑤a+b≥m（am+b）（m为任意实数）．

A、3 B、2 C、1 D、0

查看试题解析

二、填空题

11. 抛物线y＝﹣ $\frac{1}{3}$ （x﹣2）²﹣7的顶点坐标是．

查看试题解析
12. 在△ABC中，若 ${(\cos A - \frac{1}{2})}^{2} + | 1 - \tan B | = 0$ ，则∠C的大小是 °．

查看试题解析
13. 抛物线y＝x²﹣bx+1与x轴只有一个交点，那么b＝．

查看试题解析
14. 函数y= $\frac{1}{x - 3}$ + $\sqrt{x - 1}$ 的自变量x的取值范围是．

查看试题解析
15. 如图，已知圆锥底面半径为10cm，母线长为30cm，一只蚂蚁从A处出发绕圆锥侧面一周（回到原来的位置A）所爬行的最短路径为cm．

查看试题解析
16. 如图，直线 $A B$ 过原点分别交反比例函数 $y = \frac{6}{x}$ ，于A．B，过点A作 $A C ⊥ x$ 轴，垂足为C，则△ $A B C$ 的面积为．

查看试题解析
17. 如图是一个地铁站入口的双翼闸机．它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°．当双翼收起时，可以通过闸机的物体的最大宽度为cm．

查看试题解析
18. 如图，正方形OABC的边长为 $\sqrt{2}$ ，OC与y轴的正半轴的夹角为15°，点B在抛物线y＝ax²（a＞0）的图象上，则a的值为．

查看试题解析

三、解答题

19. 计算：

(1)、 $3 \tan 30 ° - \frac{1}{\cos 60 °} + \sqrt{8} \cos 45 ° + \sqrt{{(1 - \tan 60 °)}^{2}}$ ．

(2)、 $\sqrt{2} \cos 45 ° + | 1 - \sqrt{3} | - {(- \frac{1}{2})}^{- 1} - \tan 60 ° + {(π - 2020)}^{0}$ ．

查看试题解析
20. 如图，在△ABC中，AD是BC上的高，BD＝AC＝10，tanB＝ $\frac{4}{5}$ ．

(1)、求AD的长；

(2)、求cos∠C的值和S_△ABC ．

查看试题解析
21. 2020年6月26日是第33个国际禁毒日，为了解同学们对禁毒知识的掌握情况，从广安市某校800名学生中随机抽取部分学生进行调查，调查分为“不了解”“了解较少”“比较了解”“非常了解”四类，并根据调查结果绘制出如图所示的两幅不完整的统计图．请根据统计图回答下列问题：

(1)、本次抽取调查的学生共有人，估计该校800名学生中“比较了解”的学生有人．

(2)、请补全条形统计图．

(3)、“不了解”的4人中有3名男生A₁ ， A₂ ， A₃ ， 1名女生B，为了提高学生对禁毒知识的了解，对这4人进行了培训，然后随机抽取2人叹才禁毒知识的掌握情况进行检测，请用画树状图或列表的方法，求恰好抽到2名男生的概率．

查看试题解析
22. 如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB，AB，∠PBA＝∠C．

(1)、求证：PB是⊙O的切线；

(2)、连接OP，交AB于点Q，若OP＝6，⊙O的半径为2，求PB的长．

查看试题解析
23. 如图，已知反比例函数 $y_{1} = \frac{k}{x}$ 的图象与直线 $y_{2} = a x + b$ 相交于点 $A (- 2 ， 3)$ ， $B (1 ， m)$ ．

(1)、求出直线 $y = a x + b$ 的表达式．

(2)、直线写出的 $y_{1} > y_{2}$ 时， $x$ 的取值范围是．

(3)、在 $x$ 轴上有一点 $P$ 使得 $△ P A B$ 的面积为18，求出点 $P$ 的坐标．

查看试题解析
24. 如图，抛物线y＝﹣x²+bx+c与x轴交于A（2，0），B（﹣4，0）两点．
（Ⅰ）求抛物线的解析式；

（Ⅱ）若抛物线交y轴于点C，在抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出点Q的坐标；若不存在，请说明理由；

（Ⅲ）在抛物线第二象限的图象上是否存在一点P，使得△PBC的面积最大？若存在，请直接写出点P的坐标和△PBC面积的最大值；若不存在，请说明理由．

查看试题解析
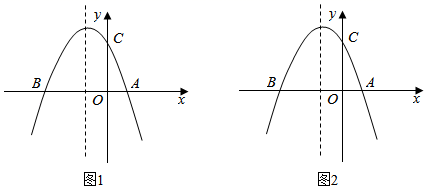25. 如图①，在Rt△AEF的内部作一个矩形ABCD，其中AB和AD分别在两直角边上，AF＝40m，AE＝30m．

(1)、如果设矩形的一边AB＝xm，那么AD边的长度如何表示？

(2)、设矩形的面积为ym² ，当x取何值时，y的值最大？最大值是多少？

(3)、如果把矩形改为如图②所示的位置，其他条件不变，那么矩形的最大面积是多少？

查看试题解析