山东省东营市河口区（五四制）2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体，它的主视图是（）

A、 B、 C、 D、

查看试题解析
2. 如图，AB是圆O的直径，CD是圆O的弦，若 $∠ C = 35 °$ ，则 $∠ A B D =$ （）

A、 $55 °$ B、 $45 °$ C、 $35 °$ D、 $65 °$

查看试题解析
3. 将抛物线y＝x²﹣4x﹣4向左平移3个单位，再向上平移3个单位，得到抛物线的表达式为（）

A、y＝（x+1）²﹣13 B、y＝（x﹣5）²﹣5 C、y＝（x﹣5）²﹣13 D、y＝（x+1）²﹣5

查看试题解析
4. 小张和小王相约去参加“抗疫情党员志愿者进社区服务”活动现在有A、B、C三个社区可供随机选择，他们两人恰好进入同一社区的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{3}$ C、 $\frac{2}{9}$ D、 $\frac{2}{3}$

查看试题解析
5. 已知点 $(- 9, y_{1})$ ， $(4, y_{2})$ ， $(- 2, y_{3})$ 都在抛物线y=ax²+m (a>0)上，则（）

A、y₁<y₂<y₃ B、y₁<y₃<y₂ C、y₃<y₂<y₁ D、y₂<y₁<y₃

查看试题解析
6. 一次函数 $y = k x - k$ 与反比例函数 $y = \frac{k}{x}$ 在同一直角坐标系中的图像可能是（）

A、 B、 C、 D、

查看试题解析
7. 如图，在5×4的正方形网格中，每个小正方形的边长都是l，△ABC的顶点都在这些小正方形的顶点上，则cos∠BAC的值为（　　）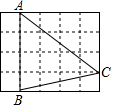

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
8. 如图， $P_{1} ， P_{2} ， P_{3}$ 是双曲线上的三点．过这三点分别作y轴的垂线，得到三个三角形 $P_{1} A_{1} O$ 、 $P_{2} A_{2} O$ 、 $P_{3} A_{3} O$ ，设它们的面积分别是 $S_{1} ， S_{2} ， S_{3}$ ，则（）．

A、S₁=S₂=S₃ B、S₂<S₁<S₃ C、S₁<S₃<S₂ D、S₁<S₂<S₃

查看试题解析
9. 已知圆锥的高为12，底面圆的半径为5，则该圆锥的侧面展开图的面积为（）

A、65π B、60π C、75π D、70π

查看试题解析
10. 如图，抛物线y＝ax²+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b²；②方程ax²+bx+c＝0的两个根是x₁＝﹣1，x₂＝3；③3a+c＜0；④当y＞0时，x的取值范围是﹣1≤x＜3；⑤当x＜0时，y随x增大而增大，其中结论正确的个数是（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

11. 抛物线 $y = 3 x^{2} + 6 x + 11$ 的顶点坐标为.

查看试题解析
12. 在一个不透明的袋中装有2个黑色小球和若干个红色小球，每个小球除颜色外都相同，每次摇匀后随机摸出一个小球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红色小球的频率稳定于0.8，则可估计这个袋中红色小球的个数约为.

查看试题解析
13. 如图，如果一只蚂蚁从圆锥底面上的点B出发，沿表面爬到母线AC的中点D处，则最短路线长为．

查看试题解析
14. 如图是一斜坡的横截面，某人沿着坡度为 $i = 1 ： \sqrt{5}$ 的斜坡从点A向上走了5米到点B处，则此时人离水平面的垂直高度为．

查看试题解析
15. 如图，小树AB在路灯O的照射下形成投影BC．若树高AB＝2m，树影BC＝3m，树与路灯的水平距离BP＝4m．则路灯的高度OP为m．

查看试题解析
16. 如图，ABCD是平行四边形，AB是⊙O的直径，点D在⊙O上，AD＝OA＝2，则图中阴影部分的面积为．

查看试题解析
17. 平放在地面上的三角形铁板ABC的一部分被沙堆掩埋，其示意图如图所示，量得∠A为54°，∠B为36°，边AB的长为2.1m，BC边上露出部分BD的长为0.9m，则铁板BC边被掩埋部分CD的长是m．（结果精确到0.1m．参考数据：sin54°≈0.81，cos54°≈0.59，tan54°≈1.38）．

查看试题解析
18. 在平面直角坐标系中，抛物线y＝x²的图象如图所示．已知A点坐标为（1，1），过点A作AA₁∥x轴交抛物线于点A₁ ，过点A₁作A₁A₂∥OA交抛物线于点A₂ ，过点A₂作A₂A₃∥x轴交抛物线于点A₃ ，过点A₃作A₃A₄∥OA交抛物线于点A₄……，依次进行下去，则点A₂₀₂₁的坐标为．

查看试题解析

三、解答题

19. 求下列各式的值：

(1)、2sin30°+3cos60°﹣4tan45°；

(2)、tan60°﹣（4﹣π）⁰+2cos30°+（ $\frac{1}{4}$ ）^﹣1

查看试题解析
20. 已知一次函数y＝kx+b与反比例函数y＝ $\frac{m}{x}$ 的图象交于A（﹣3，2）、B（1，n）两点．

(1)、求一次函数和反比例函数的表达式；

(2)、求△AOB的面积；

(3)、请观察图象，直接写出不等式kx+b≤ $\frac{m}{x}$ 的解集．

查看试题解析
21. 2019年12月以来，湖北省武汉市部分医院陆续发现不明原因肺炎病例，现已证实该肺炎为一种新型冠状病毒感染的肺炎，其传染性较强.为了有效地避免交叉感染，需要采取以下防护措施：①戴口罩；②勤洗手；③少出门；④重隔离；⑤捂口鼻；⑥谨慎吃．某公司为了解员工对防护措施的了解程度（包括不了解、了解很少、基本了解和很了解），通过网上问卷调查的方式进行了随机抽样调查（每名员工必须且只能选择一项），并将调查结果绘制成如下两幅统计图．

请你根据上面的信息，解答下列问题

(1)、本次共调查了名员工，条形统计图中 $m =$ ；

(2)、若该公司共有员工1000名，请你估计不了解防护措施的人数；

(3)、在调查中，发现有4名员工对防护措施很了解，其中有3名男员工、1名女员工.若准备从他们中随机抽取2名，让其在公司群内普及防护措施，求恰好抽中一男一女的概率．

查看试题解析
22. 如图所示，小亮在大楼 $A D$ 的观光电梯中的 $E$ 点测得大楼 $B C$ 楼底 $C$ 点的俯角为60°，此时他距地面的高度 $A E$ 为21米，电梯再上升9米到达 $D$ 点，此时测得大楼 $B C$ 楼顶 $B$ 点的仰角为45°，求大楼 $B C$ 的高度．（结果保留根号）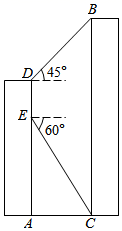

查看试题解析
23. 如图， $⊙ O$ 与 $Δ A B C$ 的AC边相切于点C ，与AB、BC边分别交于点D、E ， $D E / / O A$ ，CE是 $⊙ O$ 的直径．

(1)、求证：AB是 $⊙ O$ 的切线；

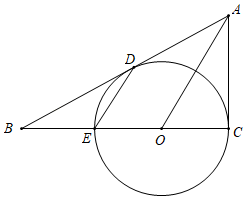(2)、若 $B D = 4 ， E C = 6 ，$ 求AC的长．

查看试题解析

24. 一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：

售价x（元/千克）	…	50	60	70	80	…
销售量y（千克）	…	100	90	80	70	…

(1)、求y与x的函数关系式；

(2)、该批发商若想获得4000元的利润，应将售价定为多少元？

(3)、该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？

查看试题解析

25. 如图，二次函数y＝ax²＋bx＋c的图象经过点（－1，4），且与直线y＝－ $\frac{1}{2}$ x＋1相交于A，B两点，A点在y轴上，过点B作BC⊥x轴，垂足为点C（－3，0）.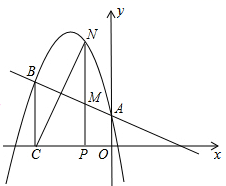

(1)、求二次函数的表达式；

(2)、点N是二次函数图象上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；

(3)、在（2）的条件下，点N在何位置时，四边形BCMN是平行四边形？并求出满足条件的N点的坐标.

查看试题解析