山东省德州市禹城市2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件为不可能事件的是(　　)

A、某射击运动员射击一次，命中靶心 B、掷一次骰子，向上的一面是5点 C、找到一个三角形，其内角和为360° D、经过城市某一有交通信号灯的路口，遇到红灯

查看试题解析
3. 关于 $x$ 一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根是0，则 $a$ 的值为（）

A、1或-1 B、1 C、-1 D、0

查看试题解析
4. 如图，放映幻灯时，通过光源，把幻灯片上的图形放大到屏幕上，若光源到幻灯片的距离为 $20 cm$ ，到屏幕的距离为 $60 cm$ ，且幻灯片中的图形的高度为 $6 cm$ ，则屏幕上图形的高度为（） $cm$ ．

A、20 B、18 C、15 D、16

查看试题解析
5. 便民商店经营一种商品，在销售过程中，发现一周利润y（元）与每件销售价x（元）之间的关系满足y=-2（x-20）²+1558，由于某种原因，价格只能15≤x≤22，那么一周可获得最大利润是（）

A、20 B、1508 C、1550 D、1558

查看试题解析
6. 将抛物线y＝x²﹣2x﹣3的图象先向右平移1个单位，再向下平移4个单位，所得图象的函数解析式为（　　）

A、y＝x²﹣3x﹣7 B、y＝x²﹣x﹣7 C、y＝x²﹣3x+1 D、y＝x²﹣4x﹣4

查看试题解析
7. 如图，点O是△ABC的内心，∠A＝62°，则∠BOC＝（）

A、59° B、31° C、124° D、121°

查看试题解析
8. 一次函数 $y_{1} = k_{1} x + b$ 和反比例函数 $y_{2} = \frac{k {}_{2}}{x} (k_{1} \cdot k_{2} \neq 0)$ 的图象如图所示，若 $y_{1} > y_{2}$ ，则 $x$ 的取值范围是（）

A、 $- 2 < x < 0$ 或 $x > 1$ B、 $- 2 < x < 1$ C、 $x < - 2$ 或 $x > 1$ D、 $x < - 2$ 或 $0 < x < 1$

查看试题解析
9. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径 $r = 1 cm$ ，扇形的圆心角 $θ = 120 °$ ，则该圆锥的母线长 $l$ 为（） $cm$ ．

A、1 B、12 C、3 D、6

查看试题解析
10. 如图所示，⊙O是正方形ABCD的外接圆，P是⊙O上不与A、B重合的任意一点，则∠APB等于（）

A、45° B、60° C、45° 或135° D、60° 或120°

查看试题解析
11. 如图，直线AB与⊙O相切于点A，弦CD∥AB，E、F为圆上的两点，且∠CDE=∠ADF，若⊙O的半径为 $\frac{5}{2}$ ，CD=4，则弦EF的长为（）

A、4 B、2 $\sqrt{5}$ C、5 D、6

查看试题解析
12. 二次函数y=ax2+bx+c（a≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x=2，下列结论：①4a+b=0；②9a+c＞3b；③8a+7b+2c＞0；④当x＞-1时，y的值随x值的增大而增大.其中正确的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 已知 $△ A B C ∽ △ D E F$ ，若 $△ A B C$ 与 $△ D E F$ 的面积比为 $9 ： 16$ ，则 $△ A B C$ 与 $△ D E F$ 的相似比为．

查看试题解析
14. 如图，△ABC是⊙O的内接三角形，AD是⊙O的直径，∠ABC=50°，则∠CAD= ．

查看试题解析
15. 如图，矩形ABCD的长AB=6cm，宽AD=3cm．O是AB的中点，OP⊥AB，两半圆的直径分别为AO与OB．抛物线y=ax²经过C、D两点，则图中阴影部分的面积是cm² ．

查看试题解析
16. 如图，已知双曲线 $y = \frac{k}{x} (k < 0)$ 经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（ $- 6$ ，4），则△AOC的面积为．

查看试题解析
17. 如图所示，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（-3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为.

查看试题解析
18. 如图，已知四边形 $A B C D$ 是矩形，把矩形沿直线 $A C$ 折叠，点 $B$ 落在点 $E$ 处，连接 $D E$ ．若 $D E ： A C = 3 ： 5$ ，则 $\frac{A D}{A B}$ 的值为．

查看试题解析

三、解答题

19. 解下列方程：

(1)、 $3 x (x - 2) = 2 (x - 2)$ ；

(2)、 $2 x^{2} - 7 x + 6 = 0$ ．

查看试题解析
20. 某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件

(1)、写出商场销售这种文具，每天所得的销售利润（元）与销售单价（元）之间的函数关系式；

(2)、求销售单价为多少元时，该文具每天的销售利润最大；

(3)、商场的营销部结合上述情况，提出了A、B两种营销方案
方案A：该文具的销售单价高于进价且不超过30元；

方案B：每天销售量不少于10件，且每件文具的利润至少为25元

请比较哪种方案的最大利润更高，并说明理由

查看试题解析
21. 小明和小亮玩一种游戏：三张大小，地都相同的卡片上分别标有数字1，2，3，现将标有数字的一面朝下，小明从中任意抽取一张，记下数字后放回洗匀，然后小亮从中任意抽取一张，计算小明和小亮抽得的两个数字之和，如果和为奇数，则小明胜，若和为偶数则小亮胜．

(1)、用列表或画树状图等方法，列出小明和小亮抽出卡片的数字之和出现的所有可能情况；

(2)、请判断该游戏对双方是否公平？并说明理由．

查看试题解析
22. 如图，四边形ABCD为正方形.点A的坐标为（0，2），点B的坐标为（0，－3），反比例函数 $y = \frac{k}{x}$ 的图象经过点C，一次函数 $y = ax + b$ 的图象经过点C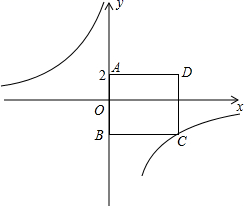，一次函数 $y = ax + b$ 的图象经过点A.

(1)、求反比例函数与一次函数的解析式；

(2)、求点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标.

查看试题解析
23. 如图，在平面直角坐标系中，已知 $△ A B C$ 的三个顶点的坐标分别为 $A (- 3 ， 5)$ ， $B (- 2 ， 1)$ ， $C (- 1 ， 3)$ ．

⑴若 $△ A B C$ 和 $△ A_{1} B_{1} C_{1}$ 关于原点 $O$ 成中心对称，写出 $△ A_{1} B_{1} C_{1}$ 的各顶点的坐标；

⑵在 $x$ 轴上求作一点 $P$ ，使 $△ P A B$ 的周长最小，请画出 $△ P A B$ ，并直接写出 $P$ 的坐标；

⑶若 $△ A B C$ 和 $△ A_{2} B_{2} C_{2}$ 关于点 $(- 1 ， 1)$ 位似，位似比为 $1 ： 2$ ，画出 $△ A_{2} B_{2} C_{2}$ （在位似中心另一侧）并写出 $△ A_{2} B_{2} C_{2}$ 各顶点的坐标．

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径， $A C$ 是弦，直线 $E F$ 经过点 $C$ ， $A D ⊥ E F$ 于点 $D$ ， $∠ D A C = ∠ B A C$ ．

(1)、求证： $E F$ 是 $⊙ O$ 的切线；

(2)、求证： $A C^{2} = A D \cdot A B$ ；

(3)、若 $⊙ O$ 的半径为 $2$ ， $∠ A C D = 30 °$ ，求图中阴影部分的面积．

查看试题解析
25.
如图，关于x的二次函数y=x²+bx+c的图象与x轴交于点A（1，0）和点B与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D

(1)、求二次函数的表达式。

(2)、在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标

(3)、有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积．

查看试题解析