山东省德州市夏津县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 下列手机手势解锁图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、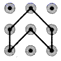 2. 用配方法解方程 时,应将其变形为( )A、 B、 C、 D、3. 下列说法正确的是( )A、“明天降雨的概率是80%”表示明天有80%的时间降雨 B、“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上 C、“彩票中奖的概率是1%”表示买100张彩票一定会中奖 D、抛一枚正方体骰子朝上面的数为奇数的概率是0.5“表示如果这个骰子抛很多很多次,那么平均每2次就有1次出现朝上面的数为奇数4. 在平面直角坐标系中,把点 向右平移8个单位得到点 ,再将点 绕原点顺时针旋转 得到点 ,则点 的坐标是( )A、 B、 C、 D、5. 如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的 ,则AO:AD的值为( )
2. 用配方法解方程 时,应将其变形为( )A、 B、 C、 D、3. 下列说法正确的是( )A、“明天降雨的概率是80%”表示明天有80%的时间降雨 B、“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上 C、“彩票中奖的概率是1%”表示买100张彩票一定会中奖 D、抛一枚正方体骰子朝上面的数为奇数的概率是0.5“表示如果这个骰子抛很多很多次,那么平均每2次就有1次出现朝上面的数为奇数4. 在平面直角坐标系中,把点 向右平移8个单位得到点 ,再将点 绕原点顺时针旋转 得到点 ,则点 的坐标是( )A、 B、 C、 D、5. 如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的 ,则AO:AD的值为( )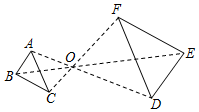 A、2:3 B、2:5 C、4:9 D、4:136. 下列命题:①长度相等的弧是等弧;②任意三点确定一个圆;③相等的圆心角所对的弦相等;④平分弦的直径垂直于弦,并且平分弦所对的两条弧;其中真命题共有( )A、0个 B、1个 C、2个 D、3个7. 已知当x>0时,反比例函数y= 的函数值随自变量的增大而减小,此时关于x的方程x2﹣2(k+1)x+k2﹣1=0的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法确定8. 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数 (x>0)的图象经过顶点B,则k的值为( )
A、2:3 B、2:5 C、4:9 D、4:136. 下列命题:①长度相等的弧是等弧;②任意三点确定一个圆;③相等的圆心角所对的弦相等;④平分弦的直径垂直于弦,并且平分弦所对的两条弧;其中真命题共有( )A、0个 B、1个 C、2个 D、3个7. 已知当x>0时,反比例函数y= 的函数值随自变量的增大而减小,此时关于x的方程x2﹣2(k+1)x+k2﹣1=0的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法确定8. 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数 (x>0)的图象经过顶点B,则k的值为( )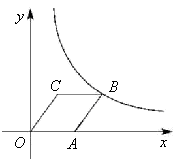 A、12 B、20 C、24 D、329. 如图,一把直尺, 60°的直角三角板和光盘如图摆放, A为 60°角与直尺交点, AB=3 ,则光盘的直径是( )
A、12 B、20 C、24 D、329. 如图,一把直尺, 60°的直角三角板和光盘如图摆放, A为 60°角与直尺交点, AB=3 ,则光盘的直径是( )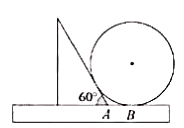 A、3 B、 C、 D、10. 某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子 恰为水面中心,安置在柱子顶端 处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,在过 的任一平面上,建立平面直角 坐标系(如图),水流喷出的高度 与水平距离 之间的关系式是 ,则下列结论错误的是( )
A、3 B、 C、 D、10. 某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子 恰为水面中心,安置在柱子顶端 处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,在过 的任一平面上,建立平面直角 坐标系(如图),水流喷出的高度 与水平距离 之间的关系式是 ,则下列结论错误的是( ) A、柱子 的高度为 B、喷出的水流距柱子 处达到最大高度 C、喷出的水流距水平面的最大高度是 D、水池的半径至少要 才能使喷出的水流不至于落在池外11. 在同一平面直角坐标系中,反比例函数y (b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是( )A、
A、柱子 的高度为 B、喷出的水流距柱子 处达到最大高度 C、喷出的水流距水平面的最大高度是 D、水池的半径至少要 才能使喷出的水流不至于落在池外11. 在同一平面直角坐标系中,反比例函数y (b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是( )A、 B、
B、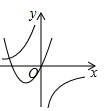 C、
C、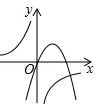 D、
D、 12. 如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3 ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE= CE;④S阴影= .其中正确的个数为( )
12. 如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3 ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE= CE;④S阴影= .其中正确的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
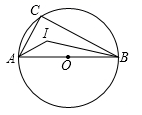
13. 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,I是△ABC的内心,则∠BIA的度数是°.
 14. 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是 .
14. 已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是 . 15. 如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB=米.
15. 如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB=米. 16. 方程x2+2kx+k2﹣2k+1=0的两个实数根x1 , x2满足x12+x22=4,则k的值为 .17. 如图,在 中, ,以点 为圆心、 长为半径画弧,交 于点 ,再分别以 为圆心、大于 的长为半径画弧,两弧交于 ,作直线 ,分别交 于点 ,则线段 的长为
16. 方程x2+2kx+k2﹣2k+1=0的两个实数根x1 , x2满足x12+x22=4,则k的值为 .17. 如图,在 中, ,以点 为圆心、 长为半径画弧,交 于点 ,再分别以 为圆心、大于 的长为半径画弧,两弧交于 ,作直线 ,分别交 于点 ,则线段 的长为 18. 二次函数 的图象如图所示,其对称轴为直线 ,与 轴的交点为 ,其中 ,有下列结论:① ;② ;③ ;④当 为任意实数时, ;⑤ .其中,正确结论的序号是
18. 二次函数 的图象如图所示,其对称轴为直线 ,与 轴的交点为 ,其中 ,有下列结论:① ;② ;③ ;④当 为任意实数时, ;⑤ .其中,正确结论的序号是
三、解答题
-
19. 在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)、“从中任意抽取1个球不是红球就是白球”是事件,“从中任意抽取1个球是黑球”是事件;(2)、从中任意抽取1个球恰好是红球的概率是;
(3)、学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
20. 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.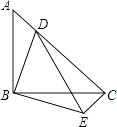 (1)、求∠DCE的度数;(2)、若AB=4,CD=3AD,求DE的长.21. 如图,在平行四边形ABCD中,连接对角线AC , 延长AB至点E , 使 ,连接DE , 分别交BC , AC交于点F , G .
(1)、求∠DCE的度数;(2)、若AB=4,CD=3AD,求DE的长.21. 如图,在平行四边形ABCD中,连接对角线AC , 延长AB至点E , 使 ,连接DE , 分别交BC , AC交于点F , G . (1)、求证: BF=CF ;
(1)、求证: BF=CF ;
(2)、若 , ,求FG的长.22. 如图,已知AC是⊙O的直径,B为⊙O上一点,D为 的中点,过D作EF∥BC交AB的延长线于点E,交AC的延长线于点F.(Ⅰ)求证:EF为⊙O的切线;
(Ⅱ)若AB=2,∠BDC=2∠A,求 的长.
 23. 某商场一种商品的进价为每件30元,售价为每件40元,每天可以销售48件,为尽快减少库存,商场决定降价促销.(1)、若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;(2)、经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?(3)、在(2)的条件下,每件商品的售价为多少元时,每天可获得最大利润?最大利润是多少元?24. 如图,一次函数 与反比例函数 ( )的图象交于 , 两点.
23. 某商场一种商品的进价为每件30元,售价为每件40元,每天可以销售48件,为尽快减少库存,商场决定降价促销.(1)、若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;(2)、经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?(3)、在(2)的条件下,每件商品的售价为多少元时,每天可获得最大利润?最大利润是多少元?24. 如图,一次函数 与反比例函数 ( )的图象交于 , 两点. (1)、求一次函数的解析式;(2)、根据图象直接写出 时 的取值范围;(3)、若 是 轴上一点,且 和 的面积相等,求点 坐标.25. 如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)、求一次函数的解析式;(2)、根据图象直接写出 时 的取值范围;(3)、若 是 轴上一点,且 和 的面积相等,求点 坐标.25. 如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点. (1)、求点A的坐标;(2)、求抛物线的解析式;(3)、点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.
(1)、求点A的坐标;(2)、求抛物线的解析式;(3)、点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.①求点P的坐标和PE的最大值.
②在直线PD上是否存在点M,使点M在以AB为直径的圆上;若存在,求出点M的坐标;若不存在,请说明理由.