山东省德州市庆云县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 下列图形中,不是中心对称图形的是( )A、圆 B、菱形 C、正十边形 D、等边三角形2. 下列说法正确的是( )A、“买一张电影票,座号是5的倍数”是必然事件 B、了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式 C、“明天降雨的概率为50%”,意味着明天一定有半天都在降雨 D、一组数据的方差越小,则这组数据的波动也越小3. 验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度)
200
250
400
500
1000
镜片焦距x(米)
0.50
0.40
0.25
0.20
0.10
A、 B、 C、 D、4. 已知二次函数 ,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )A、有最大值﹣1,有最小值﹣2 B、有最大值0,有最小值﹣1 C、有最大值7,有最小值﹣1 D、有最大值7,有最小值﹣25. 如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙ 交于点D,连结OD.若 ,则∠AOD的度数为( )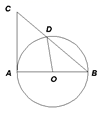 A、 B、 C、 D、6. 一次函数y=ax+b与反比列函数y= 的图象如图所示,则二次函数y=ax2+bx+c的大致图象是( )
A、 B、 C、 D、6. 一次函数y=ax+b与反比列函数y= 的图象如图所示,则二次函数y=ax2+bx+c的大致图象是( )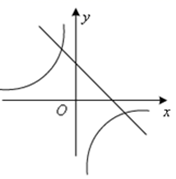 A、
A、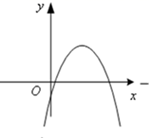 B、
B、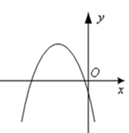 C、
C、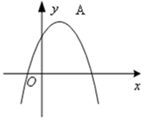 D、
D、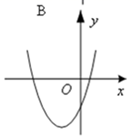 7. 如图,在△ABC中,∠CAB=55°,∠ABC=25°,在同一平面内,将△ABC绕A点逆时针旋转70°得到△ADE,连接EC,则tan∠DEC的值( )
7. 如图,在△ABC中,∠CAB=55°,∠ABC=25°,在同一平面内,将△ABC绕A点逆时针旋转70°得到△ADE,连接EC,则tan∠DEC的值( )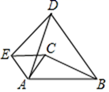 A、 B、1 C、 D、8. 一次会议上,每两个参加会议的人都相互握了一次手,有人统计一共握了45次手,这次会议到会的人数有多少人( ).A、8 B、9 C、10 D、129. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,点A(10,0),sin∠COA= .若反比例函数 经过点C,则k的值等于( )
A、 B、1 C、 D、8. 一次会议上,每两个参加会议的人都相互握了一次手,有人统计一共握了45次手,这次会议到会的人数有多少人( ).A、8 B、9 C、10 D、129. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,点A(10,0),sin∠COA= .若反比例函数 经过点C,则k的值等于( ) A、10 B、24 C、48 D、50.10. 如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )
A、10 B、24 C、48 D、50.10. 如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )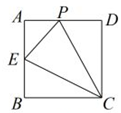 A、
A、 B、
B、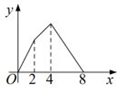 C、
C、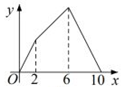 D、
D、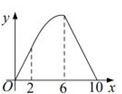 11. 如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处, .在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角 为 (点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比) ,那么建筑物AB的高度约为( )
11. 如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处, .在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角 为 (点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比) ,那么建筑物AB的高度约为( )(参考数据 , , )
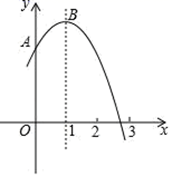
 A、65.8米 B、71.8米 C、73.8米 D、119.8米12. 如图,抛物线y=-x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
A、65.8米 B、71.8米 C、73.8米 D、119.8米12. 如图,抛物线y=-x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线y=-x2+2x+m+1与直线y=m+2有且只有一个交点;②若点M(-2,y1)、点N( ,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=-(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 .其中正确的判断有( )
 A、①②③④ B、②③④ C、①③④ D、①③
A、①②③④ B、②③④ C、①③④ D、①③二、填空题
-
13. 如果关于x的一元二次方程x2﹣4x+k=0有实数根,那么k的取值范围是.14. 一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数.连续掷两次骰子,在骰子向上的一面上,第二次出现的点数是第一次出现的点数的2倍的概率是.15. 若点A(﹣3,y1),B(﹣2,y2),C(1,y3)都在反比例函数y=﹣ 的图象上,则y1 , y2 , y3按照从小到大的顺序排列是16. 如图,四边形ABCD是矩形, , ,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是.
 17. 如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .
17. 如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .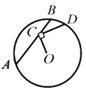 18. 如图,在Rt△ABC中,∠ABC=90°,BC=3,D为斜边AC的中点,连接BD,点F是BC边上的动点(不与点B、C重合),过点B作BE⊥BD交DF延长线交于点E,连接CE,下列结论:①若BF=CF,则CE2+AD2=DE2;②若∠BDE=∠BAC,AB=4,则CE= ;③△ABD和△CBE一定相似;④若∠A=30°,∠BCE=90°,则DE= .其中正确的是 . (填写所有正确结论的序号)
18. 如图,在Rt△ABC中,∠ABC=90°,BC=3,D为斜边AC的中点,连接BD,点F是BC边上的动点(不与点B、C重合),过点B作BE⊥BD交DF延长线交于点E,连接CE,下列结论:①若BF=CF,则CE2+AD2=DE2;②若∠BDE=∠BAC,AB=4,则CE= ;③△ABD和△CBE一定相似;④若∠A=30°,∠BCE=90°,则DE= .其中正确的是 . (填写所有正确结论的序号)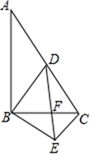
三、解答题
-
19. 计算:(1)、2sin60°tan30°+cos230°-tan45°.(2)、(2x﹣3)2﹣2(2x﹣3)﹣3=0.20. 如图所示,在平面直角坐标系中,△ABC的三个顶点分别是A(﹣2,﹣2)、B(﹣4,﹣1)、C(﹣4,﹣4).
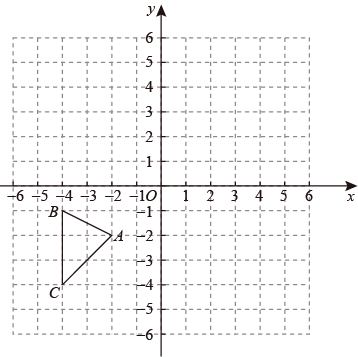
⑴画出△ABC关于原点O成中心对称的△A1B1C1;
⑵画出△ABC绕点O逆时针旋转90度的△A2B2C2;
⑶在x轴上找到一点P,使PA+PB的和最小值,求出P点坐标及最小值.
21. 为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题: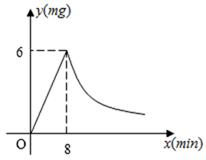 (1)、药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?(2)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?22. 如图,△ABC内接于⊙O,AB是⊙O的直径,AC=CE,连接AE交BC于点D,延长DC至F点,使CF=CD,连接AF.
(1)、药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?(2)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?22. 如图,△ABC内接于⊙O,AB是⊙O的直径,AC=CE,连接AE交BC于点D,延长DC至F点,使CF=CD,连接AF.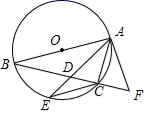 (1)、判断直线AF与⊙O的位置关系,并说明理由.(2)、若AC=10,tan∠CAE= ,求AE的长.23. “新冠”疫情蔓延全球,口罩成了人们的生活必需品,某药店销售普通口罩和N95口罩,今年8月份的进价如表:
(1)、判断直线AF与⊙O的位置关系,并说明理由.(2)、若AC=10,tan∠CAE= ,求AE的长.23. “新冠”疫情蔓延全球,口罩成了人们的生活必需品,某药店销售普通口罩和N95口罩,今年8月份的进价如表:普通口罩
N95口罩
进价(元/包)
8
20
(1)、计划N95口罩每包售价比普通口罩贵16元,7包普通口罩和3包N95口罩总售价相同,求普通口罩和N95口罩每包售价.(2)、按(1)中售价销售一段时间后,发现普通口罩的日均销售量为120包,当每包售价降价1元时,日均销售量增加20包,该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天的利润为320元,求此时普通口罩每包售价.(3)、疫情期间,该药店进货3000包N95口罩,进价不变,店长向当地医院捐赠了500包后,又打9折销售,全部售完,这批3000包的N95口罩所获利润为多少元?24. 小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.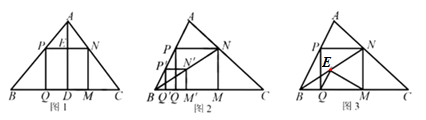 (1)、温故:如图1,在△ABC中,AD⊥BC于点D,正方形PQMN的边QM在BC上,顶点P,N分别在AB, AC上,若BC=6,AD=4,求正方形PQMN的边长.(2)、操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结B N′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN.小波把线段BN称为“波利亚线”.
(1)、温故:如图1,在△ABC中,AD⊥BC于点D,正方形PQMN的边QM在BC上,顶点P,N分别在AB, AC上,若BC=6,AD=4,求正方形PQMN的边长.(2)、操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结B N′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN.小波把线段BN称为“波利亚线”.推理:证明图2中的四边形PQMN是正方形.
(3)、拓展:在(2)的条件下,于波利业线B N上截取NE=NM,连结EQ,EM(如图3).当tan∠NBM= 时,猜想∠QEM的度数,并尝试证明.请帮助小波解决“温故”、“推理”、“拓展”中的问题.
25. 如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.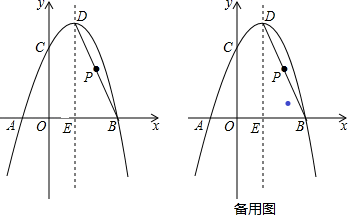 (1)、求经过A,B,C三点的抛物线的函数表达式;(2)、点Q在该抛物线的对称轴上,若△BCQ是以BC为直角边的直角三角形,求点Q的坐标;(3)、若P为BD的中点,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、N、G为顶点的四边形是正方形时,请求出点M的坐标.
(1)、求经过A,B,C三点的抛物线的函数表达式;(2)、点Q在该抛物线的对称轴上,若△BCQ是以BC为直角边的直角三角形,求点Q的坐标;(3)、若P为BD的中点,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、N、G为顶点的四边形是正方形时,请求出点M的坐标.