山东省德州市临邑县2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是中心对称图形又是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 如图，一个几何体由5个大小相同、棱长为1的小正方体搭成，下列说法正确的是（）．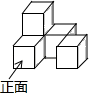

A、主视图的面积为4 B、左视图的面积为4 C、俯视图的面积为3 D、三种视图的面积都是4

查看试题解析
3. 将函数 $y = 2 x^{2}$ 的图象向左平移1个单位，再向上平移3个单位，可得到的抛物线是（）

A、 $y = 2 {(x - 1)}^{2} - 3$ B、 $y = 2 {(x - 1)}^{2} + 3$ C、 $y = 2 {(x + 1)}^{2} - 3$ D、 $y = 2 {(x + 1)}^{2} + 3$

查看试题解析
4. 某果园2011年水果产量为100吨，2013年水果产量为144吨，求该果园水果产量的年平均增长率．设该果园水果产量的年平均增长率为x，则根据题意可列方程为（）

A、144（1﹣x）²=100 B、100（1﹣x）²=144 C、144（1+x）²=100 D、100（1+x）²=144

查看试题解析
5. 下列说法中，正确的是（）

A、所有的等腰三角形都相似 B、所有的菱形都相似 C、所有的矩形都相似 D、所有的等腰直角三角形都相似

查看试题解析
6. 在Rt△ABC中，∠C=90°，当已知∠A和a时，求c，应选择的关系式是（）

A、c = $\frac{a}{\sin A}$ B、c = $\frac{a}{\cos A}$ C、c = a·tanA D、c = $\frac{a}{\tan A}$

查看试题解析
7. 如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD＝55°，则∠BCD的度数为（）

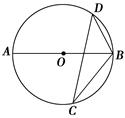A、35° B、45° C、55° D、75°

查看试题解析
8. 两个相似多边形的面积之比为1：3，则它们的周长之比为（）

A、1：3 B、1：9 C、 $1 ： \sqrt{3}$ D、2：3

查看试题解析
9. 如图，直径为10的 $⊙ A$ 经过点 $C (0 ， 5)$ 和点 $O (0 ， 0)$ ， $B$ 是 $y$ 轴右侧 $⊙ A$ 优弧上一点，则 $\tan ∠ O B C$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{4}{5}$

查看试题解析
10. 关于x的一元二次方程（k–1）x²–2x＋3=0有两个不相等的实数根，则k的取值范围是（）

A、k< $\frac{4}{3}$ B、k< $\frac{4}{3}$ 且k≠1 C、0<k< $\frac{4}{3}$ D、k≠1

查看试题解析
11. 函数 $y = \frac{k}{x}$ 与 $y = k x^{2} - k (k \neq 0)$ 在同一直角坐标系中的图象大致是下图中的（）

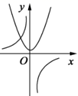A、 B、 C、 D、

查看试题解析
12. 如图，AB是⊙O的直径，直线DE与⊙O相切于点C，过A，B分别作AD⊥DE，BE⊥DE，垂足为点D，E，连接AC，BC，若AD＝ $\sqrt{3}$ ，CE＝3，则 $\overset{⌢}{A C}$ 的长为（　　）

A、 $\frac{2 \sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{3}$ π C、 $\frac{\sqrt{3}}{2}$ π D、 $\frac{2 \sqrt{3}}{3}$ π

查看试题解析

二、填空题

13. $\cos 60^{0}$ = .

查看试题解析
14. 小强将10盒蔬菜的标签全部撕掉了．现在每个盒子看上去都一样．但是她知道有七盒菠菜，三盒豆角．她随机地拿出一盒并打开它．盒子里面是豆角的概率是．

查看试题解析
15. 如图，⊙O的直径CD＝10，弦AB＝8，AB⊥CD，垂足为M，则CM的长为．

查看试题解析
16. 方程 $x^{2} - 6 x + 4 = 0$ 的两个实根分别为 $x_{1}$ ， $x_{2}$ ，那么 $x_{1} x_{2} - x_{1} - x_{2}$ 的值为．

查看试题解析
17. 如图，将△ABC绕点C旋转60°得到△A′B′C′，已知AC=6，BC=4，则线段AB扫过图形（阴影部分）的面积为（结果保留π）.

查看试题解析
18. 如图，在反比例函数 $y = \frac{2}{x} (x > 0)$ 的图象上，有点 $P_{1}$ ， $P_{2}$ ， $P_{3}$ ， $P_{4}$ 它们的横坐标依次为1，2，3，4．分别过这些点作 $x$ 轴与 $y$ 轴 $y = \frac{2}{x}$ 的垂线，图中所构成的阴影部分的面积从左到右依次为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ，则 $S_{1} + S_{2} + S_{3} =$ ．

查看试题解析

三、解答题

19. “一方有难，八方支援”．武汉新冠病毒牵动着全国人民的心，我市某医院甲、乙、丙三位医生和 $A$ 、 $B$ 两名护士报名支援武汉．

(1)、若从甲、乙、丙三位医生中随机选一位医生，求恰好选中医生甲的概率；

(2)、若从甲、乙、丙三位医生和 $A$ 、 $B$ 两名护士中随机选一位医生和一名护士，求恰好选中医生甲和护士 $A$ 的概率．

查看试题解析
20. 用适当方法解方程：

(1)、 $2 x^{2} - 6 x + 1 = 0$ ；

(2)、 $x^{2} - 2 x - 8 = 0$ ．

查看试题解析
21. 新年前夕，信业超市在销售中发现：某服装平均每天可售出20套，每件盈利40元．为了迎接新年，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存．经市场调查发现：如果每套降价1元，那么平均每天就可多售出2套．

(1)、要想平均每天在销售服装上盈利1200元，那么每套应降价多少元？

(2)、商场要想每天获取最大利润，每套应降价多少元？

查看试题解析
22. 已知一次函数 $y = \frac{2}{3} x + 2$ 的图象分别与坐标轴相交于 $A$ 、 $B$ 两点（如图所示），与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象相交于 $C$ 点．

(1)、直接写出 $A$ 、 $B$ 两点的坐标；

(2)、作 $C D ⊥ x$ 轴，垂足为 $D$ ，如果 $O B$ 是 $△ A C D$ 的中位线，求反比例函数 $y = \frac{k}{x} (k > 0)$ 的关系式．

(3)、请根据图象直接写出在第一象限内，反比例函数值大于一次函数值时自变量 $x$ 的取值范围．

查看试题解析
23. 如图， $B D$ 为 $△ A B C$ 外接圆 $⊙ O$ 的直径，且 $∠ B A E = ∠ C$ ．

(1)、求证： $A E$ 与 $⊙ O$ 相切于点 $A$ ；

(2)、若 $A E // B C$ ， $B C = 2 \sqrt{3}$ ， $A C = 2$ ，求 $⊙ O$ 的直径．

查看试题解析
24. 已知：如图，点 $C ， D$ 在线段 $A B$ 上， $△ P C D$ 是等边三角形．

(1)、当 $A C ， C D ， D B$ 满足怎样的关系式时 $△ A C P ∽ △ P D B$ ；

(2)、当 $△ A C P ∽ △ P D B$ 时，求 $∠ A P B$ 的度数．

查看试题解析
25. 如图1，已知抛物线 $y = a x^{2} + b x + c$ 经过 $A (- 3 ， 0)$ ， $B (1 ， 0)$ ， $C (0 ， 3)$ 三点，其顶点为 $D$ ，对称轴与 $x$ 轴交于点 $H$ ．

(1)、求该抛物线的解析式；

(2)、若点 $P$ 是该抛物线对称轴上的一个动点，求 $△ P B C$ 周长的最小值；[结果保留根号]

(3)、如图2，若 $E$ 是线段 $A D$ 上的一个动点（ $E$ 与 $A$ 、 $D$ 不重合），过 $E$ 点作平行于 $y$ 轴的直线交抛物线于点 $F$ ，交 $x$ 轴于点 $G$ ，设点 $E$ 的横坐标为 $m$ ， $△ A D F$ 的面积为 $S$ ．
①求 $S$ 与 $m$ 的函数关系式；

② $S$ 是否存在最大值？若存在，求出最大值及此时点 $E$ 的坐标；若不存在，请说明理由．

查看试题解析