山东省滨州市无棣县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
1. 事件“对于实数 , ”是( )A、随机事件 B、必然事件 C、确定事件 D、不可能事件2. 如图,由5个相同正方体组合而成的几何体,它的俯视图是( )
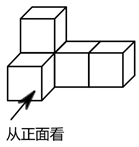 A、
A、 B、
B、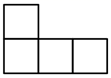 C、
C、 D、
D、 3. 如图,沿 方向修山路,为了加快施工进度,要在小山的另一边同时施工,从 上的一点 取 , 米, ,使 、 、 在一条直线上,那么开挖点 与 的距离是( )
3. 如图,沿 方向修山路,为了加快施工进度,要在小山的另一边同时施工,从 上的一点 取 , 米, ,使 、 、 在一条直线上,那么开挖点 与 的距离是( ) A、 米 B、 米 C、 米 D、 米4. 如图, 是 的直径, 为圆上两点, ,则 等于( )
A、 米 B、 米 C、 米 D、 米4. 如图, 是 的直径, 为圆上两点, ,则 等于( ) A、 B、 C、 D、5. 已知反比例函数 ,下列结论中错误的是( )A、函数图象经过点 B、函数图象分别位于第二、四象限 C、 随 的增大而增大 D、若 ,则6. 如图,在 中,点 、 分别在 、 上, ,若 , , 、四边形 的面积分别为 , ,则 的值为( )
A、 B、 C、 D、5. 已知反比例函数 ,下列结论中错误的是( )A、函数图象经过点 B、函数图象分别位于第二、四象限 C、 随 的增大而增大 D、若 ,则6. 如图,在 中,点 、 分别在 、 上, ,若 , , 、四边形 的面积分别为 , ,则 的值为( ) A、 B、 C、 D、7. 一元二次方程x2﹣5x+6=0的解为( )A、x1=2,x2=﹣3 B、x1=﹣2,x2=3 C、x1=﹣2,x2=﹣3 D、x1=2,x2=38. 下列命题说法正确的有( )
A、 B、 C、 D、7. 一元二次方程x2﹣5x+6=0的解为( )A、x1=2,x2=﹣3 B、x1=﹣2,x2=3 C、x1=﹣2,x2=﹣3 D、x1=2,x2=38. 下列命题说法正确的有( )①三点确定一个圆;②长度相等的弧是等弧;③等边三角形都相似;④直角三角形都相似;⑤平分弦的直径垂直于弦.⑥一条弧所对的圆周角等于它所对的圆心角的一半.
A、1个 B、2个 C、3个 D、4个9. 在正方形 中,分别以 、 为圆心,以正方形的边长2为半径画弧,则图中阴影部分的面积为( ) A、 B、 C、2 D、10. 如图,在矩形 中, , ,点 在 边上, ,垂足为 .若 ,则线段 的长为( )
A、 B、 C、2 D、10. 如图,在矩形 中, , ,点 在 边上, ,垂足为 .若 ,则线段 的长为( ) A、6 B、8 C、4 D、1011. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A、6 B、8 C、4 D、1011. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )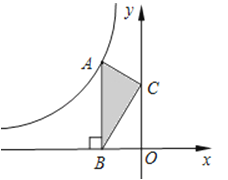 A、3 B、﹣3 C、6 D、﹣612. 如图,抛物线 与 轴交于点 和 ,与 轴交于点 .下列结论:
A、3 B、﹣3 C、6 D、﹣612. 如图,抛物线 与 轴交于点 和 ,与 轴交于点 .下列结论:① ,② ,③ ,④ ,其中正确的结论为( )
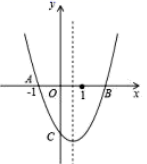 A、①②③ B、②③ C、③④ D、①②③④
A、①②③ B、②③ C、③④ D、①②③④二、填空题
-
13. 若 是方程 的一个根,则 的值为14. 如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为米.
 15. 已知点 , 在反比例函数 的图象上,则 (填“>”、“<”或“=”).16. 如图, 是 的直径, , 切 于点 ,线段 交 于点 .连接 ,若 ,则劣弧 的长度是
15. 已知点 , 在反比例函数 的图象上,则 (填“>”、“<”或“=”).16. 如图, 是 的直径, , 切 于点 ,线段 交 于点 .连接 ,若 ,则劣弧 的长度是 17. 在抛物线形拱桥中,以抛物线的对称轴为y轴,顶点为原点建立如图所示的平面直角坐标系,抛物线解析式为y=ax2 , 水面宽AB=6m,AB与y轴交于点C,OC=3m,当水面上升1m时,水面宽为m.
17. 在抛物线形拱桥中,以抛物线的对称轴为y轴,顶点为原点建立如图所示的平面直角坐标系,抛物线解析式为y=ax2 , 水面宽AB=6m,AB与y轴交于点C,OC=3m,当水面上升1m时,水面宽为m. 18. 在-2, , ,2,3五个数中随机选取一个数作为二次函数 中 的值,则该二次函数图象开口向上的概率是19. 如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地. ,斜坡 长 ,斜坡 的坡比为12∶5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿 至少向右移 时,才能确保山体不滑坡.(取 )
18. 在-2, , ,2,3五个数中随机选取一个数作为二次函数 中 的值,则该二次函数图象开口向上的概率是19. 如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地. ,斜坡 长 ,斜坡 的坡比为12∶5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿 至少向右移 时,才能确保山体不滑坡.(取 ) 20. 如图,在△ABC中,D是边BC上的一点,以AD为直径的⊙O交AC于点E,连接DE.若⊙O与BC相切,∠ADE=55°,则∠C的度数为 .
20. 如图,在△ABC中,D是边BC上的一点,以AD为直径的⊙O交AC于点E,连接DE.若⊙O与BC相切,∠ADE=55°,则∠C的度数为 .
三、解答题
-
21.(1)、计算: .(2)、已知点 在抛物线 上,求出抛物线与 轴的交点.22. 为了备战五月份初三物理、化学实验操作考试,我县某初中学校对九年级学生进行了模拟训练,物理、化学各有4个不同的操作实验题目,物理实验题目用号码①、②、③、④代表,化学实验题目用字母 、 、 、 表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.(1)、请用树形图法或列表法,表示某个同学抽签的各种可能情况.(2)、吴爱棣同学对物理的②、③和化学的 、 号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少?23.(1)、如图,在矩形 中, 是 的中点, 于点 .若 , ,求 的长.
 (2)、如图,在 中, , ,点 在边 上, , ,求 的值.
(2)、如图,在 中, , ,点 在边 上, , ,求 的值.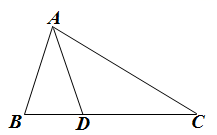 24. 如图,已知反比例函数 与一次函数 的图象相交于点 、点 ,且点 的横坐标为2,点 的纵坐标为-2,过点 作 轴于点 , 的面积为4.
24. 如图,已知反比例函数 与一次函数 的图象相交于点 、点 ,且点 的横坐标为2,点 的纵坐标为-2,过点 作 轴于点 , 的面积为4. (1)、求反比例函数和一次函数的解析式;(2)、若一次函数 的图像与 轴交于点 ,求 的度数.(3)、结合图像直接写出,当 时, 的取值范围.25. 已知,如图, 是 的直径,点 为 上一点, 于点 ,交 于点 , 与 交于点 ,点 为 的延长线上一点,且 .
(1)、求反比例函数和一次函数的解析式;(2)、若一次函数 的图像与 轴交于点 ,求 的度数.(3)、结合图像直接写出,当 时, 的取值范围.25. 已知,如图, 是 的直径,点 为 上一点, 于点 ,交 于点 , 与 交于点 ,点 为 的延长线上一点,且 . (1)、求证: 是 的切线;(2)、求证:(3)、若 , ,求 的长.26. 某农贸市场销售一种农产品,平均每天可售出40箱,每箱盈利50元,为了扩大销售,减少库存农贸市场决定降价销售,经调查,每箱降价1元时,平均每天可多卖出2箱.(1)、若农贸市场销售这种农产品每天盈利2400元,尽量减少库存,每箱应降价多少元?(2)、试说明每箱农产品降价多少元时,该农贸市场销售这种农产品每天盈利最多,最多是多少元?27. 如图,已知 , 是 内部的一点,过点 作 ,垂足为点 , , ,动点 , 同时从 点出发,点 以 秒的速度沿 方向运动,点 以 秒的速度沿 方向运动, 与 交于点 ,连接 ,当点 到达点 时,点 随之停止运动.设运动时间为 秒 .
(1)、求证: 是 的切线;(2)、求证:(3)、若 , ,求 的长.26. 某农贸市场销售一种农产品,平均每天可售出40箱,每箱盈利50元,为了扩大销售,减少库存农贸市场决定降价销售,经调查,每箱降价1元时,平均每天可多卖出2箱.(1)、若农贸市场销售这种农产品每天盈利2400元,尽量减少库存,每箱应降价多少元?(2)、试说明每箱农产品降价多少元时,该农贸市场销售这种农产品每天盈利最多,最多是多少元?27. 如图,已知 , 是 内部的一点,过点 作 ,垂足为点 , , ,动点 , 同时从 点出发,点 以 秒的速度沿 方向运动,点 以 秒的速度沿 方向运动, 与 交于点 ,连接 ,当点 到达点 时,点 随之停止运动.设运动时间为 秒 . (1)、当 秒时, 与 是否相似?请说明理由;(2)、在运动过程中,试判断 与 的位置关系,并说明理由.(3)、连接 ,在运动过程中,是否存在某一时刻 ,使得 ?若存在,请求出此时 的值;若不存在,请说明理由.
(1)、当 秒时, 与 是否相似?请说明理由;(2)、在运动过程中,试判断 与 的位置关系,并说明理由.(3)、连接 ,在运动过程中,是否存在某一时刻 ,使得 ?若存在,请求出此时 的值;若不存在,请说明理由.