江苏省南通市2021-2022学年七年级上学期数学期中考试试卷

试卷更新日期：2021-11-16 类型：期中考试

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 2021年5月15日，我国“天问一号”探测器在火星成功着陆．火星具有和地球相近的环境，与地球最近时候的距离约 $55000000 km$ ．将数字55000000用科学记数法表示为（）

A、 $0.55 \times 10^{8}$ B、 $5.5 \times 10^{7}$ C、 $5.5 \times 10^{6}$ D、 $55 \times 10^{6}$

查看试题解析
3. 如图，检测4个足球，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数.从轻重的角度看，最接近标准的是（）.

A、-3.5 B、+2.5 C、-0.6 D、+0.7

查看试题解析
4. 下列各数： $- \frac{7}{3}$ ，6，-2，-0.9，0， $- 3 \frac{1}{4}$ ，其中负分数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 下列计算正确的是（）

A、 $5 a^{2} - a^{2} = 5$ B、 $2 a + 3 b = 5 a b$ C、 $a b^{2} + 3 b a^{2} = 4 a b^{2}$ D、 $- 3 (a - b) = - 3 a + 3 b$

查看试题解析
6. 一滴墨水洒在数轴上，根据图中标出的数值判断墨迹盖住的整数个数是（）

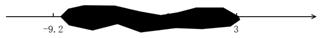A、14 B、13 C、12 D、11

查看试题解析
7. 下列各组数中，互为相反数的是（）

A、（-2）³与-2³ B、2与 $| - 2 |$ C、-1与（-1）² D、2与 $\frac{1}{2}$

查看试题解析
8. 若 $a^{2} = 4$ ， $| b | = 3$ ，且 $a b < 0$ ，则 $a - b$ 的值为（）

A、1或-5 B、-1或5 C、1或-1 D、5或-5

查看试题解析
9. 若多项式 $4 x^{2} - 3 x + 7$ 与多项式 $5 x^{3} + (m - 2) x^{2} - 2 x + 3$ 相加后，结果不含 $x^{2}$ 项，则常数m的值是（）

A、-2 B、2 C、5 D、6

查看试题解析
10. 把2021个正整数1，2，3，4，…，2021按如图方式列成一个表.用图中阴影所示方式框住表中任意4个数，这四个数的和可能是（）

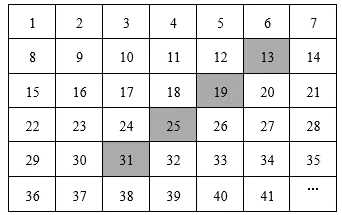A、192 B、190 C、188 D、186

查看试题解析

二、填空题

11. 若家用电冰箱冷藏室的温度是4℃，冷冻室的温度要比冷藏室低22℃，则冷冻室的温度是.

查看试题解析
12. 用四舍五入法，取近似值：6.5378≈（精确到0.01）.

查看试题解析
13. 某单项式的系数为 $\frac{1}{2}$ ，只含字母x，y，且次数是3次，写出一个符合条件的单项式可以是.

查看试题解析
14. 若单项式 $4 x^{4} y^{n + 5}$ 与单项式 $- 5 x^{m} y^{3}$ 的和仍为单项式，则这两个单项式的和等于.

查看试题解析
15. 某轮船在静水中的速度是50km/h，水流速度是akm/h.若该轮船顺水航行2h，逆水航行1.5h，共航行km.

查看试题解析
16. 观察下面两行数：
-2，4，-8，16，-32，64，…

1，7，-5，19，-29，67，…根据你发现的规律，取每行数的第9个数，它们的和等于.

查看试题解析
17. 下列说法：①若a为有理数，且 $a \neq 0$ ，则 $a < a^{2}$ ；②若 $\frac{1}{a} = a$ ，则 $a = 1$ ；③若 $a^{3} + b^{3} = 0$ ，则a，b互为相反数；④若 $| a | = - a$ ，则 $a < 0$ .其中正确说法是（填序号）.

查看试题解析
18. 现有一列整数，第一个数为1，第二个数为x（x为正整数）.以后每一个数都由它前一个数与再前一个数差的绝对值得到.如第三个数是由x与1差的绝对值得到，即为 $| x - 1 |$ ，第四个数是由 $| x - 1 |$ 与x差的绝对值得到，即为 $| | x - 1 | - x |$ ，…，依此类推要使这列数的前101个数中恰好有30个0，则 $x =$ .

查看试题解析

三、解答题

19. 计算：

(1)、 $- 6 + (- 1.2) + 3 - (- \frac{2}{5})$

(2)、 $- 2^{3} \div (- \frac{3}{2}) \times \frac{4}{9}$

查看试题解析
20. 化简：

(1)、 $2 x + (5 x - 3 y) - (- 5 y + 3 x)$

(2)、 $3 (4 x^{2} - 3 x + 2) - 2 (1 - 4 x^{2} - x)$

查看试题解析
21. 小明坚持跑步锻炼身体，他以30分钟为基准，将连续七天的跑步时间（单位：分钟）记录如下：12，－9，11，－7，13，15，－5（超过30分钟的部分记为“＋”.不足30分钟的部分记为“－”）

(1)、跑步时间最长的一天比最短的一天多跑几分钟？

(2)、若小明跑步的平均速度为每分钟0.15千米，请你计算这七天他共跑了多少千米？

查看试题解析
22. 已知 $M = 3 x^{2} - 2 x y - 3$ ， $N = 4 x^{2} - 2 x y + 1$ .

(1)、当 $x = - 1$ ， $y = \frac{5}{4}$ 时，求 $4 M - (2 M + 3 N)$ 的值；

(2)、试判断M、N的大小关系并说明理由.

查看试题解析
23. 有这样一道题“如果代数式 $5 a + 3 b$ 的值为-4，那么代数式 $2 (a + b) + 4 (2 a + b)$ 的值是多少？”爱动脑筋的汤同学解题过程如下：
原式 $= 2 a + 2 b + 8 a + 4 b = 10 a + 6 b = 2 (5 a + 3 b) = 2 \times (- 4) = - 8$ .

汤同学把 $5 a + 3 b$ 作为一个整体求解整体思想是中学数学解题中的一种重要思想方法，请仿照上面的解题方法，完成下面问题：

（简单应用）

(1)、已知 $a^{2} + a = 3$ ，则 $2 a^{2} + 2 a + 2021 =$ ；

(2)、已知 $a - 2 b = - 3$ ，求 $3 (a - b) - 7 a + 11 b + 5$ 的值；

(3)、（拓展提高）
已知 $a^{2} + 2 a b = - 5$ ， $a b - 2 b^{2} = - 3$ ，求代数式 $2 a^{2} + \frac{5}{2} a b + 3 b^{2}$ 的值.

查看试题解析

24. 学校举办诗歌颂祖国活动，需要定制一批奖品颁发给表现突出的同学，每份奖品包含纪念徽章与纪念品各一个，现有两家供应商可以提供纪念徽章设计、制作和纪念品制作业务，报价如下：

	纪念徽章设计费	纪念徽章制作费	纪念品费用
甲供应商	300元	3元/个	18元/个
乙供应商	免设计费	4.5元/个	不超过100个时，20元/个；超过100个时，其中100单价仍是20元/个，超出部分打八折

(1)、现学校需要定制x份奖品.请你算一算，选择甲供应商和乙供应商，分别需要支付多少费用（用含x的代数式表示，结果需化简）；

(2)、如果学校需要定制150份奖品，请你通过计算说明选择哪家供应商比较省钱.

查看试题解析

25. 阅读材料，并回答问题.
钟表中蕴含着有趣的数学运算，不用负数也可以作减法.例如现在是10点钟，4小时以后是几点钟？虽然10+4=14，但在表盘上看到的是2点钟.如果用符号“㊉”表示钟表上的加法，则10㊉4=2.若问2点钟之前4小时是几点钟，就得到钟表上的减法概念，用符号“㊀”表示钟表上的减法（注：我们用0点钟代替12点钟）

由上述材料可知：

(1)、7㊉9= ， 1㊀5=；

(2)、在有理数运算中，相加得零的两个数互为相反数，如果在钟表运算中沿用这个概念，则8的相反数是：直接判断有理数减法法则“减去一个数等于加上这个数的相反数”在钟表运算中是否仍然成立（填“是”或“否”）；

(3)、规定在钟表运算中也有0<1<2<3<4<5<6<7<8<9<10<11，对于钟表上的任意数字a，b，c，若 $a < b$ ，判断a㊉c<b㊉c是否一定成立，若一定成立，说明理由；若不一定成立，写出一组反例，并结合反例加以说明.

查看试题解析
26. 如图，数轴上点A，B所对应的数是-4，4.对于关于x的代数式N，我们规定：当有理数x在数轴上所对应的点为A，B之间（包括点A，B）的任意一点时，代数式N的最大值小于等于4，最小值大于等于-4，则称代数式N是线段AB的“和谐”代数式，例如，对于关于x的代数式 $| x |$ ，当 $x = \pm 4$ 时，代数式 $| x |$ 取得最大值4；当 $x = 0$ 时，代数式 $| x |$ 取得最小值0，所以代数式 $| x |$ 是线段AB的“和谐”代数式.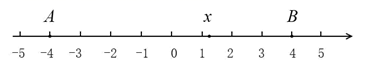

问题：

(1)、关于x的代数式 $| x - 2 |$ ，当有理数x在数轴上所对应的点为A，B之间（包括点A，B）的任意一点时，取得的最大值是，最小值是.所以代数式 $| x - 2 |$ （填“是”或“不是”）线段AB的“和谐”代数式.

(2)、关于x的代数式 $| x + 3 | + a$ 是线段AB的“和谐”代数式，则有理数a的最大值是，最小值是.

(3)、以下关于x的代数式：① $\frac{1}{2} x - \frac{5}{2}$ ；② $x^{2} + 1$ ；③ $| x + 2 | - | x - 1 | - 1$ .其中是线段AB的“和谐”代数式的是_▲_，并证明（只需要证明是线段AB的“和谐”代数式的式子，不是的不需证明）.

查看试题解析