山东省滨州市惠民县2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、单选题
-
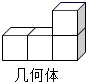
1. 一元二次方程 的解是( )A、-2 B、2 C、±4 D、±22. 如图所示的几何体的主视图是( )
 A、
A、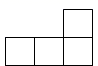 B、
B、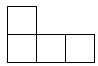 C、
C、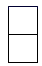 D、
D、 3. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、4. 用配方法解关于 的一元二次方程 ,配方后的方程可以是( )A、 B、 C、 D、5. 菱形的两条对角线长分别是6和8,则此菱形的周长是( )A、5 B、20 C、24 D、326. 如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )米.
3. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、4. 用配方法解关于 的一元二次方程 ,配方后的方程可以是( )A、 B、 C、 D、5. 菱形的两条对角线长分别是6和8,则此菱形的周长是( )A、5 B、20 C、24 D、326. 如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )米. A、asin40° B、acos40° C、atan40° D、7. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、8. 定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”,如“947”就是一个“V数”.若十位上的数字为2,则从1,3,4,5中任选两数,能与2组成“V数”得概率是( )A、 B、 C、 D、9. 如图,已知 中, , ,点 在 边上,把 沿 翻折使 与 重合,得 ,则 与 重叠部分的面积为( )
A、asin40° B、acos40° C、atan40° D、7. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、8. 定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”,如“947”就是一个“V数”.若十位上的数字为2,则从1,3,4,5中任选两数,能与2组成“V数”得概率是( )A、 B、 C、 D、9. 如图,已知 中, , ,点 在 边上,把 沿 翻折使 与 重合,得 ,则 与 重叠部分的面积为( )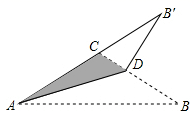 A、 B、 C、 D、10. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
A、 B、 C、 D、10. 如图, 中, ,点D在 上, .若 ,则 的长度为( )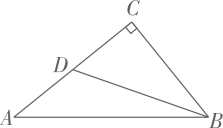 A、 B、 C、 D、411. 如图,在 中, .边 在x轴上,顶点 的坐标分别为 和 .将正方形 沿x轴向右平移当点E落在 边上时,点D的坐标为( )
A、 B、 C、 D、411. 如图,在 中, .边 在x轴上,顶点 的坐标分别为 和 .将正方形 沿x轴向右平移当点E落在 边上时,点D的坐标为( )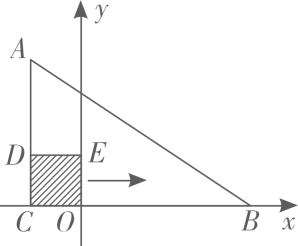 A、 B、 C、 D、12. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1 , x2 , 其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a<0;④b2+8a>4ac,其中正确的有( )
A、 B、 C、 D、12. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1 , x2 , 其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a<0;④b2+8a>4ac,其中正确的有( )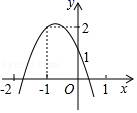 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 方程 的解是 .14. 把一枚均匀的硬币连续抛掷两次,两次正面朝上的概率是 .15. 如图,在Rt△ABC中,∠C=90°,D是AB的中点,ED⊥AB交AC于点E.设∠A=α,且tanα= ,则tan2α= .
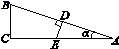 16. 一等腰三角形,底边长是18厘米,底边上的高是18厘米,现在沿底边依次从下往上画宽度均为3厘米的矩形,画出的矩形是正方形时停止,则这个矩形是第个.17. 如图,在矩形 中, 的平分线 与 交于点 , 的平分线 与 交于点 ,若 , ,则 的长是 .
16. 一等腰三角形,底边长是18厘米,底边上的高是18厘米,现在沿底边依次从下往上画宽度均为3厘米的矩形,画出的矩形是正方形时停止,则这个矩形是第个.17. 如图,在矩形 中, 的平分线 与 交于点 , 的平分线 与 交于点 ,若 , ,则 的长是 .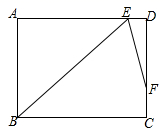 18. 如图,已知动点A在函数 (x>o)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=4:9时,图中的阴影部分的面积等于
18. 如图,已知动点A在函数 (x>o)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=4:9时,图中的阴影部分的面积等于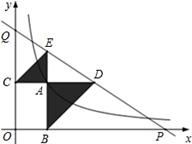
三、解答题
-
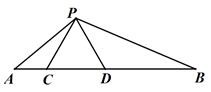
19. 计算: .20. 解方程: .21. 已知:如图,点C,D在线段AB上,△PCD是等边三角形,且AC=1,CD=2,DB=4.
求证:△ACP∽△PDB.
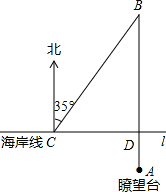
 22. 现有5个质地、大小完全相同的小球上分别标有数字–1,–2,1,2,3.先将标有数字–2,1,3的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现分别从两个盒子里各随机取出一个小球.(1)、请利用列表或画树状图的方法表示取出的两个小球上数字之和所有可能的结果;(2)、求取出的两个小球上的数字之和等于0的概率.23. 某海滨浴场东西走向的海岸线可以近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号,他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.
22. 现有5个质地、大小完全相同的小球上分别标有数字–1,–2,1,2,3.先将标有数字–2,1,3的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现分别从两个盒子里各随机取出一个小球.(1)、请利用列表或画树状图的方法表示取出的两个小球上数字之和所有可能的结果;(2)、求取出的两个小球上的数字之和等于0的概率.23. 某海滨浴场东西走向的海岸线可以近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号,他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
 24. 阅读下列内容,并答题:我们知道,计算 边形的对角线条数公式为: .如果一个 边形共有20条对角线,那么可以得到方程 .整理得 ;解得 或 , 为大于等于3的整数, 不合题意,舍去. ,即多边形是八边形.根据以上内容,问:(1)、若一个多边形共有9条对角线,求这个多边形的边数;(2)、小明说:“我求得一个多边形共有10条对角线”,你认为小明同学说法正确吗?为什么?25. 已知:如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于一、三象限内的A.B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC= .
24. 阅读下列内容,并答题:我们知道,计算 边形的对角线条数公式为: .如果一个 边形共有20条对角线,那么可以得到方程 .整理得 ;解得 或 , 为大于等于3的整数, 不合题意,舍去. ,即多边形是八边形.根据以上内容,问:(1)、若一个多边形共有9条对角线,求这个多边形的边数;(2)、小明说:“我求得一个多边形共有10条对角线”,你认为小明同学说法正确吗?为什么?25. 已知:如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象交于一、三象限内的A.B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC= .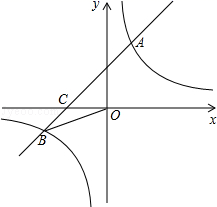 (1)、求该反比例函数和一次函数的解析式;(2)、在x轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求出点E的坐标.26. 如图,在 中, , 是中线, ,一个以点 为顶点的45°角绕点 旋转,使角的两边分别与 , 的延长线相交,交点分别为点 , , 与 交于点 , 与 交于点 .
(1)、求该反比例函数和一次函数的解析式;(2)、在x轴上有一点E(O点除外),使得△BCE与△BCO的面积相等,求出点E的坐标.26. 如图,在 中, , 是中线, ,一个以点 为顶点的45°角绕点 旋转,使角的两边分别与 , 的延长线相交,交点分别为点 , , 与 交于点 , 与 交于点 . (1)、如图①,若 ,求证: ;(2)、如图②,在 绕点 旋转的过程中:若 , ,
(1)、如图①,若 ,求证: ;(2)、如图②,在 绕点 旋转的过程中:若 , ,①求线段 的长;
②求 的长.
27. 综合与探究在平面直角坐标系中,抛物线 经过点 ,点 为抛物线的顶点,点 在 轴上,且 ,直线 与抛物线在第一象限交于点 ,如图.
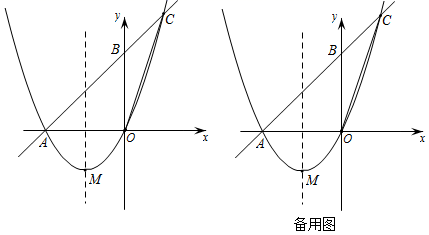 (1)、求抛物线的解析式;(2)、直线 的函数解析式为 , 点 的坐标为 , .(3)、在 轴上找一点 ,使得 的周长最小.请求出点 的坐标;(4)、在抛物线的对称轴上是否存在点 ,使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、直线 的函数解析式为 , 点 的坐标为 , .(3)、在 轴上找一点 ,使得 的周长最小.请求出点 的坐标;(4)、在抛物线的对称轴上是否存在点 ,使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.