青海省海东市2020-2021学年九年级上学期期末数学试题
试卷更新日期:2021-11-16 类型:期末考试
一、填空题
-
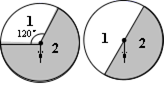
1. 分别有数字0,﹣1,2,1,﹣3的五张卡片,除数字不同外其他均相同,从中任抽一张,那么抽到负数的概率是 .2. 把二次函数y=x2﹣4x+3化成y=a(x﹣h)2+k的形式是 .3. 已知方程2x2+4x﹣3=0的两根分别为x1、x2 , 则x1+x2= , x1x2=.4. 如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为4的概率是 .
 5. 若3a2﹣a﹣2=0,则5+2a﹣6a2=6. 时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是.7. 二次函数y=x2+2x﹣4的图象的对称轴是 , 顶点坐标是 .8. 已知圆锥的底面圆半径为3cm,高为4cm,则母线长为cm,圆锥的侧面积为cm2 .9. 对于实数a,b,定义运算“※”如下:a※b=a2﹣ab,例如,5※3=52﹣5×3=10.若(x+1)※(x﹣2)=6,则x的值为 .10. 某型号的冰箱连续两次降价,每台售价由原来的2370元降到了1160元,若设平均每次降价的百分率为 ,则可列出的方程是.11. 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为cm.
5. 若3a2﹣a﹣2=0,则5+2a﹣6a2=6. 时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是.7. 二次函数y=x2+2x﹣4的图象的对称轴是 , 顶点坐标是 .8. 已知圆锥的底面圆半径为3cm,高为4cm,则母线长为cm,圆锥的侧面积为cm2 .9. 对于实数a,b,定义运算“※”如下:a※b=a2﹣ab,例如,5※3=52﹣5×3=10.若(x+1)※(x﹣2)=6,则x的值为 .10. 某型号的冰箱连续两次降价,每台售价由原来的2370元降到了1160元,若设平均每次降价的百分率为 ,则可列出的方程是.11. 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为cm. 12. 已知等边△ABC的边长为4,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,点D是AC边的中点,连接DQ,则DQ的最小值是 .
12. 已知等边△ABC的边长为4,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,点D是AC边的中点,连接DQ,则DQ的最小值是 .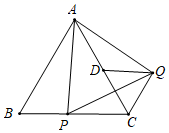
二、单选题
-
13. 下列图案中既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
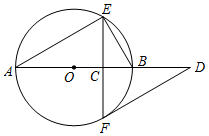
D、 14. 抛物线y=x2﹣5x+6与x轴的交点情况是( )A、有两个交点 B、只有一个交点 C、没有交点 D、无法判断15. 如图, 为 的直径, 为 上两点,若 ,则 的大小为( ).
14. 抛物线y=x2﹣5x+6与x轴的交点情况是( )A、有两个交点 B、只有一个交点 C、没有交点 D、无法判断15. 如图, 为 的直径, 为 上两点,若 ,则 的大小为( ).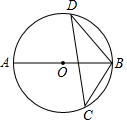 A、60° B、50° C、40° D、20°16. 若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为( ).A、-1 B、2 C、-1或2 D、-1或2或117. 关于x的一元二次方程(m﹣1)x2﹣x+m2﹣1=0的一个解是0,则m的值为( )A、0 B、±1 C、1 D、-118. 对于抛物线y=﹣ (x﹣5)2+3,下列说法错误的是( )A、对称轴是直线x=5 B、函数的最大值是3 C、开口向下,顶点坐标(5,3) D、当x>5时,y随x的增大而增大19. 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1 , 若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
A、60° B、50° C、40° D、20°16. 若函数y=(a﹣1)x2﹣4x+2a的图象与x轴有且只有一个交点,则a的值为( ).A、-1 B、2 C、-1或2 D、-1或2或117. 关于x的一元二次方程(m﹣1)x2﹣x+m2﹣1=0的一个解是0,则m的值为( )A、0 B、±1 C、1 D、-118. 对于抛物线y=﹣ (x﹣5)2+3,下列说法错误的是( )A、对称轴是直线x=5 B、函数的最大值是3 C、开口向下,顶点坐标(5,3) D、当x>5时,y随x的增大而增大19. 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1 , 若点B1在线段BC的延长线上,则∠BB1C1的大小为( )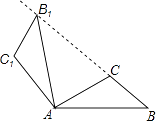 A、70° B、80° C、84° D、86°20. 已知二次函数y=ax2﹣4ax+3与x轴交于A、B两点,与y轴交于点C,若S△ABC=3,则a=( )A、 B、 C、﹣1 D、1
A、70° B、80° C、84° D、86°20. 已知二次函数y=ax2﹣4ax+3与x轴交于A、B两点,与y轴交于点C,若S△ABC=3,则a=( )A、 B、 C、﹣1 D、1三、解答题
-
21. 解方程:x2+4x﹣2=0.22. 已知x1 , x2是关于x的一元二次方程x2﹣2(m+1)x+m2+5=0的两个实数根,求m的取值范围.23. 正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
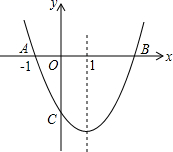
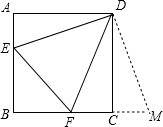 (1)、求证:EF=CF+AE;(2)、当AE=2时,求EF的长.24. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)、求证:EF=CF+AE;(2)、当AE=2时,求EF的长.24. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
⑴画出△ABC关于x轴对称的△A1B1C1 ,
⑵画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2 ,
⑶△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴并写出对称轴;
⑷△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
25. 在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,篮球1个,若从中任意摸出一个球,摸到球是红球的概率为 .(1)、求袋中黄球的个数;(2)、第一次任意摸出一个球(不放回),第二次再摸出一个球,求两次摸到球的颜色是红色与黄色这种组合(不考虑红、黄球顺序)的概率.26. 益群精品店以转件21元的价格购进一批商品,该商品可以白行定价,若每件商B品位价a元,可卖出(350-10a)件,但物价局限定每件商品的利润率不得超过20%,商店计划要盈利400元,求每件商品应定价多少元?