四川省宜宾市南溪区2021-2022学年九年级上学期数学期中考试试卷
试卷更新日期:2021-11-16 类型:期中考试
一、单选题
-
1. 使二次根式 有意义的 的取值范围是( )A、 B、 C、 D、2. 下列二次根式中与 是同类二次根式的是( )A、 B、 C、 D、3. 下列运算中正确的是( )A、 B、 C、 D、4. 下列根式是最简二次根式的是( )A、 B、 C、 D、5. 若方程x2+x-1=0的两实根为α、β,那么下列式子正确的是( )A、α+β=1 B、αβ=1 C、α2+β2=2 D、 + =16. 一元二次方程x2+x+1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定7. 已知m,n是一元二次方程 的两个实数根,则代数式 的值等于( )A、2019 B、2020 C、2021 D、20228.
如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2 , 则道路的宽应为多少米?设道路的宽为x米,则可列方程为( )
 A、100×80﹣100x﹣80x=7644 B、(100﹣x)(80﹣x)+x2=7644 C、(100﹣x)(80﹣x)=7644 D、100x+80x=3569. 如图, ,直线 、 与 、 、 分别相交于 、 、 和 、 、 .若 , ,则 的长是( )
A、100×80﹣100x﹣80x=7644 B、(100﹣x)(80﹣x)+x2=7644 C、(100﹣x)(80﹣x)=7644 D、100x+80x=3569. 如图, ,直线 、 与 、 、 分别相交于 、 、 和 、 、 .若 , ,则 的长是( ) A、 B、 C、 D、10. 如图,在比例尺为1:150 000的某城市地图上,若量得A、B两所学校的距离是4.2cm,则A、B两所学校的实际距离是( )
A、 B、 C、 D、10. 如图,在比例尺为1:150 000的某城市地图上,若量得A、B两所学校的距离是4.2cm,则A、B两所学校的实际距离是( ) A、630米 B、6300米 C、8400米 D、4200米11. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A、630米 B、6300米 C、8400米 D、4200米11. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( ) A、
A、 B、
B、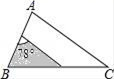 C、
C、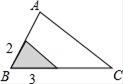 D、
D、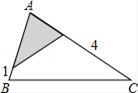 12. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分AC,点 H 为垂足,设 AB=x,AD=y,则y 关于x 的函数关系用图象大致可以表示为 ( )
12. 在四边形 ABCD 中,∠B=90°,AC=4,AB∥CD,DH 垂直平分AC,点 H 为垂足,设 AB=x,AD=y,则y 关于x 的函数关系用图象大致可以表示为 ( )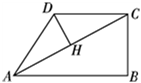 A、
A、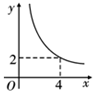 B、
B、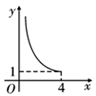 C、
C、 D、
D、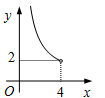
二、填空题
-
13. 已知 = ,那么 等于 .14. 比较大小: (填“>”或“<”或“=”).15. 若关于x的一元二次方程 有一个根是0,则m= .16. 关于x的方程x2+2x﹣m=0有两个相等的实数根,则m= .
17. 如图,某小区车库出入口的栏杆短臂 长1m,长臂 长8m,当短臂外端 下降0.5m时,长臂外端 升高. 18. 如果关于x的一元二次方程 有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”,以下关于“倍根方程”的说法,正确的有(填序号).
18. 如果关于x的一元二次方程 有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”,以下关于“倍根方程”的说法,正确的有(填序号).①方程 是“倍根方程”;
②若 是“倍根方程”,则 ;
③若 满足 ,则关于x的方程 是“倍根方程”;
④若方程 是“倍根方程”,则必有 .
三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、(2)、(3)、21.(1)、先化简,再求值: ,其中 .(2)、已知 , ,求 和 的值.22. 现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.(1)、求该快递公司投递总件数的月平均增长率;
(2)、如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?23. 已知 是关于 的一元二次方程 的两个实数根.(1)、求m的取值范围;(2)、若 ,求 的值;24. 如图,在△ABC中,AD⊥BC且AD2=BD•CD. (1)、求证:∠BAC=90°;(2)、若BD=2,AC= ,求CD的长.25. 如图,在矩形 中, cm, cm.点 、 、 分别从点 、 、 三点同时出发,沿矩形的边按逆时针方向移动.点 、 的速度均为2cm/s,点F的速度为4cm/s,当点 追上点 (即点 与点 重合)时,三个点随之停止移动.设移动开始后第 秒时, 的面积为 (cm2).
(1)、求证:∠BAC=90°;(2)、若BD=2,AC= ,求CD的长.25. 如图,在矩形 中, cm, cm.点 、 、 分别从点 、 、 三点同时出发,沿矩形的边按逆时针方向移动.点 、 的速度均为2cm/s,点F的速度为4cm/s,当点 追上点 (即点 与点 重合)时,三个点随之停止移动.设移动开始后第 秒时, 的面积为 (cm2). (1)、当 秒时, 的值是多少?(2)、当 等于多少秒时, 的值是18cm2;(3)、若点 在矩形的边 上移动,当 为何值时,以点 、 、 为顶点的三角形与以点 、 、 为顶点的三角形相似?请说明理由.
(1)、当 秒时, 的值是多少?(2)、当 等于多少秒时, 的值是18cm2;(3)、若点 在矩形的边 上移动,当 为何值时,以点 、 、 为顶点的三角形与以点 、 、 为顶点的三角形相似?请说明理由.