四川省巴中市平昌县云台片区2021-2022学年九年级上学期数学期中考试试卷

试卷更新日期：2021-11-16 类型：期中考试

进入出卷网下载

一、单选题

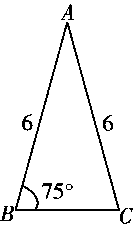
1. 二次根式 $\sqrt{6 - x}$ 中x的取值范围是（）

A、x≥6 B、x≤6 C、x＜6 D、x＞6

查看试题解析
2. 在平面直角坐标系中，将点 $P (- 3 ， 2)$ 向右平移3个单位得到点 $P^{'}$ ，则点 $P^{'}$ 关于x轴的对称点的坐标为（）

A、 $(0 ， - 2)$ B、 $(0 ， 2)$ C、 $(- 6 ， 2)$ D、 $(- 6 ， - 2)$

查看试题解析
3. 用配方法解方程x²+10x+9=0，下列变形正确的是（）

A、（x+5）²=16 B、（x+10）²=91 C、（x﹣5）²=34 D、（x+10）²=109

查看试题解析
4. 若 $\sqrt{75}$ 与最简二次根式 $\sqrt{m + 1}$ 是同类二次根式，则m的值为（）

A、7 B、11 C、2 D、1

查看试题解析
5. 下列图形中，与如图所示的 $△$ ABC相似的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，已知△OAB与△OA′B′是相似比为 1∶2 的位似图形，点O为位似中心，若△OAB内一点P(x，y)与△OA′B′内一点P′是一对对应点，则点P′的坐标为(　　)

A、(－x，－y) B、(－2x，－2y) C、(－2x，2y) D、(2x，－2y)

查看试题解析
7. 已知m、n是方程x²﹣2x﹣1=0的两根，且（m²﹣2m+a）（3n²﹣6n﹣7）=8，则a的值为（　　）

A、﹣5 B、5 C、﹣3 D、3

查看试题解析
8. 某小区有一块矩形的草地，这块草地的宽为 $(\sqrt{6} - \sqrt{2}) m$ ，为美化小区环境，打算为这块矩形草地围上低矮栅栏.若所需栅栏的总长为 $(10 \sqrt{6} - 2 \sqrt{2}) m$ ，那么这块草地的面积为（）

A、 $24 m^{2}$ B、 $(24 - 8 \sqrt{3}) m^{2}$ C、 $48 m^{2}$ D、 $(48 - 16 \sqrt{3}) m^{2}$

查看试题解析
9. 如图，在一块长为30m，宽为24m的矩形空地上，修建同样宽的两条互相垂直的小路，其余部分建成花园，已知小路的占地面积为53m² ，那么小路的宽为（）

A、1m B、1.5m C、2m D、2.5m

查看试题解析
10. 如图， $R t Δ A B O$ 中， $∠ A O B = 90 °$ ， $A O = 3 B O$ ，点 $B$ 在反比例函数 $y = \frac{2}{x}$ 的图象上， $O A$ 交反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象于点 $C$ ，且 $O C = 2 C A$ ，则 $k$ 的值为（）

A、-2 B、-4 C、-6 D、-8

查看试题解析

二、填空题

11. 化简： $\sqrt{{(3 - \sqrt{10})}^{2}}$ ＝.

查看试题解析
12. 在△ABC和△DEF中， $\frac{A B}{D E} = \frac{B C}{E F}$ ．要使△ABC∽△DEF，还需要添加一个条件，那么这个条件可以是（只需填写一个正确的答案）．

查看试题解析
13. 把两个含 $30 °$ 角的直角三角板按如图所示拼接在一起，点 $E$ 为 $A D$ 的中点，连结 $B E$ 交 $A C$ 于点 $F$ .则 $\frac{A F}{A C}$ =.

查看试题解析
14. 填空9x²﹣8x+=9（x）²=（3x﹣）².

查看试题解析
15. 关于x的方程ax²＋2x－a＋2＝0(a是已知数)有以下三个结论：①当a＝0时，方程只有一个实数解；②当a≠0时，方程有两个不相等的实数解；③当a是任意实数时，方程总有负数解，其中正确的是(填序号).

查看试题解析
16. 在函数y= $\frac{\sqrt{4 x - 3}}{x - 2}$ 中，自变量x的取值范围是．

查看试题解析
17. 某商品经过两次连续降价，每件售价由原来的60元降到了40元.设平均每次降价的百分率为x，则可列方程是 .

查看试题解析
18. 若方程 $(m - 2) x^{| m |} + 4 m x + 1 = 0$ 是关于x的一元二次方程，则m的值为.

查看试题解析
19. 若方程ax²+bx+c=0（a≠0）满足9a﹣3b+c=0，则方程必有一根为．

查看试题解析
20. 请阅读下列材料：
问题：已知方程x²＋x－1＝0，求一个一元二次方程，使它的根分别是已知方程根的2倍.

解：设所求方程的根为y，则y＝2x，所以x＝ $\frac{y}{2}$ .把x＝ $\frac{y}{2}$ 代入已知方程，得 ${(\begin{array}{l} \frac{y}{2} \end{array})}^{2}$ ＋ $\frac{y}{2}$ －1＝0.化简，得y²＋2y－4＝0，故所求方程为y²＋2y－4＝0.这种利用方程根的代换求新方程的方法，我们称为“换根法”.请用阅读材料提供的“换根法”求新方程(要求：把所求方程化为一般形式)：已知方程x²＋x－1＝0，求一个一元二次方程，使它的根分别为已知方程根的倒数，则所求方程为.

查看试题解析

三、解答题

21. 计算：

(1)、﹣1⁴+ $\frac{1}{\sqrt{2} - 1} + \sqrt{3}$ （ $\sqrt{3} - \sqrt{6}$ ）+ $\sqrt{8}$

(2)、(x－2)(x－4)＝12

(3)、2x²＋5x＋3＝0；

(4)、 $\sqrt{18}$ － $\sqrt{8}$ ＋( $\sqrt{3}$ ＋1)( $\sqrt{3}$ －1)；

(5)、 ${(3 x - 2)}^{2} - 5 (3 x - 2) + 4 = 0$

(6)、 $(3 x - 4) (2 x - 4) = 0$

查看试题解析
22. 已知x=2+ $\sqrt{3}$ ，y=2﹣ $\sqrt{3}$ ，
求代数式的值：

(1)、x²﹣y²

(2)、 $\frac{x}{y} - \frac{y}{x}$

查看试题解析
23. 如图， $△$ ABC的中线BE，CD相交于点O，F、G分别是BO、CO的中点，连结DF，EG，试猜想DF与EG有怎样的数量关系和位置关系？并证明你的猜想.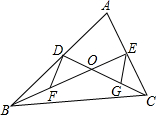

查看试题解析
24. 设x₁ ， x₂是一元二次方程ax²+bx+c=0（a≠0）的两根.

(1)、试推导x₁+x₂=- $\frac{b}{a}$ ，x₁·x₂= $\frac{c}{a}$ ；

(2)、求代数式a（x₁³+x₂³）+b（x₁²+x₂²）+c（x₁+x₂）的值.

查看试题解析
25. 已知关于x的一元二次方程x²+2（m﹣1）x+m²﹣4=0有两个不相等的实数根.

(1)、求m的取值范围；

(2)、若m为正整数，且该方程的两个根都是整数，求m的值.

查看试题解析
26. 某水果商场经销一种高档水果，原价每千克50元，连续两次降价后每千克32元，若每每次下降的百分率相同．

(1)、求每次下降的百分率；

(2)、若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，且要尽快减少库存，那么每千克应涨价多少元？

查看试题解析
27. 已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE=DF ， CE的延长线交DA的延长线于点G ， CF的延长线交BA的延长线于点H ．

(1)、求证：△BEC∽△BCH；

(2)、如果BE²=AB•AE ，求证：AG=DF ．

查看试题解析
28. 如图（1），P 为△ABC 所在平面上一点，且∠APB=∠BPC=∠CPA=120°，则点 P 叫做△ABC 的费马点.

(1)、如果点 P 为锐角△ABC 的费马点，且∠ABC=60°.
①求证：△ABP∽△BCP；

②若 PA=3，PC=4，则 PB= .

(2)、已知锐角△ABC，分别以 AB、AC 为边向外作正△ABE 和正△ACD，CE 和 BD相交于 P 点.如图（2）
①求∠CPD 的度数；

②求证：P 点为△ABC 的费马点.

查看试题解析